机器学习模型| 监督学习| KNN | 决策树

分类模型

• K近邻
• 逻辑斯谛回归
• 决策树

K近邻（KNN）

最简单最初级的分类器，就是将全部的训练数据所对应的类别都记录下来，当测试对象的属性和某个训练对象的属性完全匹配时，便可以对其进行分类
K近邻（k-nearest neighbour, KNN）是一种基本分类方法，通过测量不同特征值之间的距离进行分类。它的思路是：如果一个样本在特征空间中的k个最相似（即特征空间中最邻近）的样本中的大多数属于某一个类别，则该样本也属于这个类别，其中K通常是不大于20的整数；
KNN算法中，所选择的邻居都是已经正确分类的对象

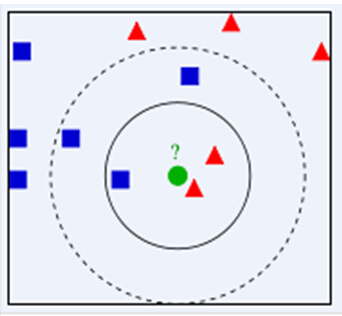
绿色圆(测试数据)要被决定赋予哪个类，是红色三角形还是蓝色四方形？
　　如果K=3(距离绿色圆最近的3个)，由于红色三角形所占比例为2/3，绿色圆将被赋予红色三角形那个类，
　　如果K=5(距离绿色圆最近的5个)，由于蓝色四方形比例为3/5，因此绿色圆被赋予蓝色四方形类;

KNN算法的结果很大程度取决于K的选择。

KNN距离计算
KNN中，通过计算对象间距离来作为各个对象之间的非相似性指标，避免了对象之间的匹配问题，在这里距离一般使用欧氏距离或曼哈顿距离：

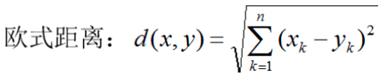
（一般选择曼哈顿距离）

KNN算法
在训练集中数据和标签已知的情况下，输入测试数据，将测试数据的特征与训练集中对应的特征进行相互比较，找到训练集中与之最为相似的前K个数据，则该测试数据对应的类别就是K个数据中出现次数最多的那个分类，其算法的描述为：

• 计算测试数据与各个训练数据之间的距离；
• 按照距离的递增关系进行排序；
• 选取距离最小的K个点；
• 确定前K个点所在类别的出现频率；
• 返回前K个点中出现频率最高的类别作为测试数据的预测分类。

代码的实现：

### 0.引入依赖
import numpy as np
import pandas as pd

# 这里直接引入sklearn里的数据集，iris鸢尾花
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split  # 切分数据集为训练集和测试集
from sklearn.metrics import accuracy_score # 计算分类预测的准确率

  基于sklearn的iris数据集及简介

附:

print(iris.data.shape) #data对应了样本的4个特征，150行4列(150, 4)
print(iris.data[:5]) # 显示样本特征的前5行
print(iris.target.shape) # target对应了样本的类别（目标属性），150行1列
print(iris.target) # 显示所有样本的目标属性； iris的每个样本都包含了品种信息，即目标属性（第5列，也叫target或label）
===>
(150, 4)
[[5.1 3.5 1.4 0.2]
 [4.9 3.  1.4 0.2]
 [4.7 3.2 1.3 0.2]
 [4.6 3.1 1.5 0.2]
 [5.  3.6 1.4 0.2]]
(150,)
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
 2 2]

iris = load_iris()
df = pd.DataFrame(data = iris.data, columns = iris.feature_names)
df['class'] = iris.target
df['class'] = df['class'].map({0: iris.target_names[0], 1: iris.target_names[1], 2: iris.target_names[2]})
df.head(10)

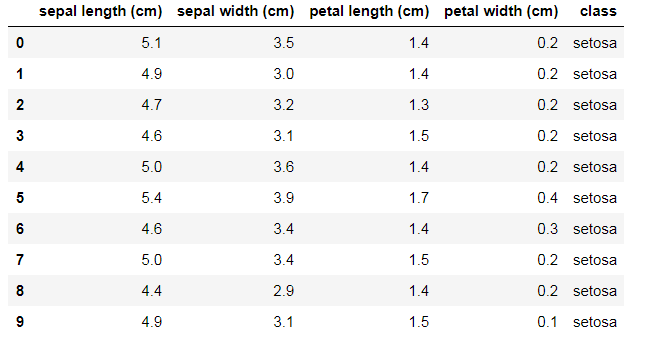
df.describe()

x = iris.data
y = iris.target.reshape(-1,1)
print(x.shape, y.shape)
===>
(150, 4) (150, 1)

# 划分训练集和测试集
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3, random_state=35, stratify=y)

print(x_train.shape, y_train.shape)
print(x_test.shape, y_test.shape)
==>
(105, 4) (105, 1)
(45, 4) (45, 1)

核心算法实现

# 距离函数定义
def l1_distance(a, b):
    return np.sum(np.abs(a-b), axis=1) #曼哈顿距离, 向量的绝对值，一阶距离
def l2_distance(a, b):
    return np.sqrt( np.sum((a-b) ** 2, axis=1) ) #二阶距离

# 分类器实现
class kNN(object):
    # 定义一个初始化方法，__init__ 是类的构造方法
    def __init__(self, n_neighbors = 1, dist_func = l1_distance):
        self.n_neighbors = n_neighbors
        self.dist_func = dist_func

    # 训练模型方法
    def fit(self, x, y):
        self.x_train = x
        self.y_train = y

    # 模型预测方法
    def predict(self, x):
        # 初始化预测分类数组
        y_pred = np.zeros( (x.shape[0], 1), dtype=self.y_train.dtype )

        # 遍历输入的x数据点，取出每一个数据点的序号i和数据x_test
        for i, x_test in enumerate(x):
            # x_test跟所有训练数据计算距离
            distances = self.dist_func(self.x_train, x_test)

            # 得到的距离按照由近到远排序，取出索引值
            nn_index = np.argsort(distances)

            # 选取最近的k个点，保存它们对应的分类类别
            nn_y = self.y_train[ nn_index[:self.n_neighbors] ].ravel()

            # 统计类别中出现频率最高的那个，赋给y_pred[i]
            y_pred[i] = np.argmax( np.bincount(nn_y) )

        return y_pred

### 3. 测试

# 定义一个knn实例
knn = kNN(n_neighbors = 3)
# 训练模型
knn.fit(x_train, y_train)
# 传入测试数据，做预测
y_pred = knn.predict(x_test)
print("分类准确率：{:.5f}%".format(accuracy_score(y_test,y_pred)*100))
==>
分类准确率：93.33333%

测试L1和L2距离对准确率是否有比较大的影响？

# 定义一个knn实例
knn = kNN()
# 训练模型
knn.fit(x_train, y_train)

# 保存结果list
result_list = []

# 针对不同的参数选取，做预测
for p in [1, 2]:
    knn.dist_func = l1_distance if p == 1 else l2_distance

    # 考虑不同的k取值，步长为2
    for k in range(1, 10, 2):
        knn.n_neighbors = k
        # 传入测试数据，做预测
        y_pred = knn.predict(x_test)
        # 求出预测准确率
        accuracy = accuracy_score(y_test, y_pred)
        result_list.append([k, 'l1_distance' if p == 1 else 'l2_distance', accuracy])
df = pd.DataFrame(result_list, columns=['k', '距离函数', '预测准确率'])  #选择 5 l2_distance的距离
df

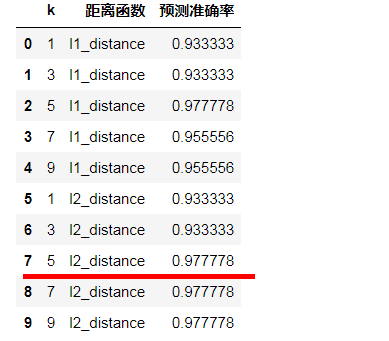
可得出 ：

5

l2_distance

0.977778

KNN=5时，距离选取l2_distance，它的准确率是最高的。

决策树

决策树是一种简单高效并且具有强解释性的模型，广泛应用于数据分析领域。其本质是一颗自上而下的由多个判断节点组成的树；

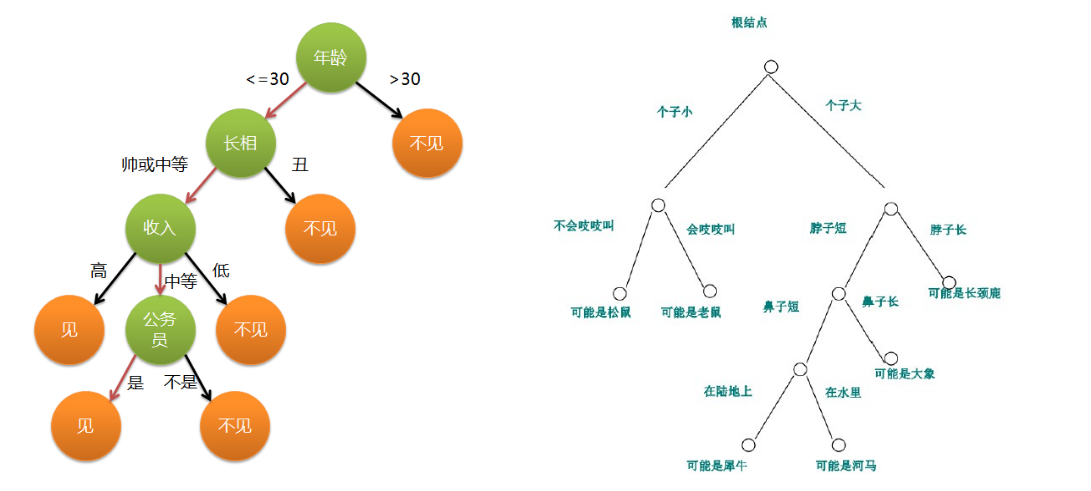
决策树示例： 

预测小明今天是否会出门打球

     

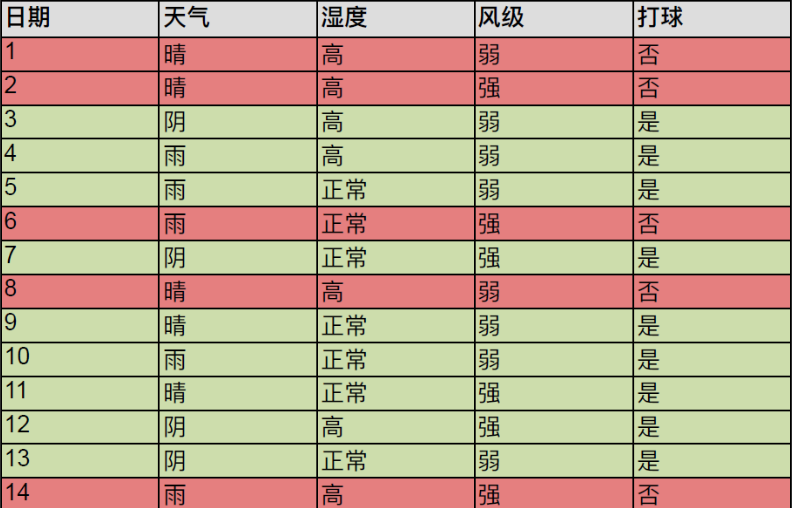
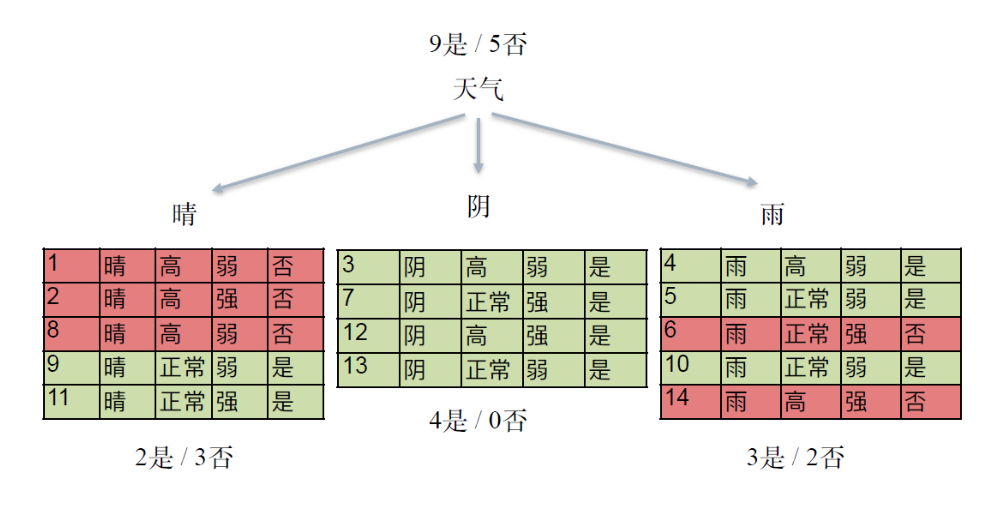
决策树与 if-then 规则

• 决策树可以看作一个 if-then 规则的集合

• 由决策树的根节点到叶节点的每一条路径，构建一条规则：路径上内部节点的特征对应着规则的条件（condition），叶节点对应规则的结论
• 决策树的 if-then 规则集合有一个重要性质：互斥并且完备。这就是说，每个实例都被一条规则（一条路径）所覆盖，并且只被这一条规则覆盖

决策树中的 Condition 是什么？

• Condition 的确定过程就是特征选择的过程；

决策树的目标：

• 决策树学习的本质，是从训练数据集中归纳出一组 if-then 分类规则
• 与训练集不相矛盾的决策树，可能有很多个，也可能一个也没有；所以我们需要选择一个与训练数据集矛盾较小的决策树
• 另一角度，我们可以把决策树看成一个条件概率模型，我们的目标是将实例分配到条件概率更大的那一类中去；
• 从所有可能的情况中选择最优决策树，是一个NP完全问题，所以我们通常采用启发式算法求解决策树，得到一个次最优解
• 采用的算法通常是递归地进行以下过程：选择最优特征，并根据该特征对训练数据进行分割，使得各个子数据集都有一个最好的分类

特征选择：

• 特征选择就是决定用哪个特征来划分特征空间

随机变量：
　　随机变量（random variable）的本质是一个函数，是从样本空间的子集到实数的映射，将事件转换成一个数值

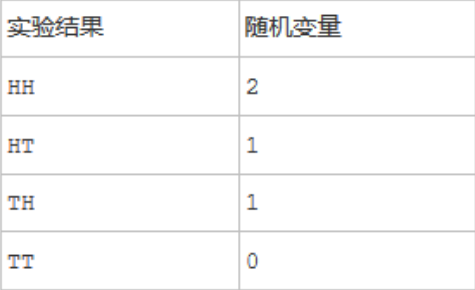
根据样本空间中的元素不同(即不同的实验结果)，随机变量的值也将随机产生。可以说，随机变量是“数值化”的实验结果
在现实生活中，实验结果是描述性的词汇，比如 “硬币的正面”、“反面”。在数学家眼里，这些文字化的叙述太过繁琐，所以拿数字来代表它们

熵
　　熵（entropy）用来衡量随机变量的不确定性；变量的不确定性越大，熵也就越大

设X是一个取有限个值的离散随机变量，其概率分布为：

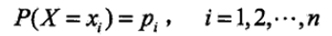
则随机变量X的熵定义为：

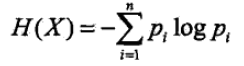
通常，上式中的对数以2为底或者以e为底（自然对数），这时熵的单位分别称为比特（bit）或纳特（nat）。

当随机变量只取两个值，例如 1,0 时，则 X 的分布为：

熵为：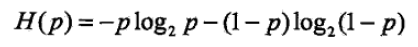   

这时，熵H(p)随概率p变化的曲线如下图所示（单位为比特）：

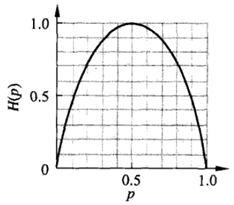
熵的示例

给三个球分类

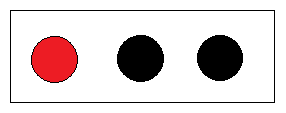
• 显然一眼就可以看出把红球独自一组，黑球一组；
• 那么从熵的观点来看，是什么情况呢？

初始状态的熵：  E(三个球) = - 1/3 * log( 1/3 ) - 2/3 * log( 2/3 ) = 0.918

①第一种分类方法是一个红球、一个黑球一组，另一个黑球自己一组：

• 在红黑一组中有红球和黑球, 红黑球各自出现的概率是 1/2.
• 在另一组 100% 出现黑球, 红球的概率是 0

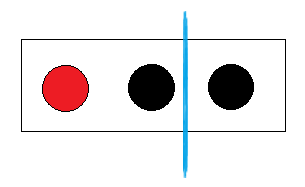
E(红黑|黑) = E(红黑) + E(黑) = - 1/2 * log( 1/2 ) - 1/2 * log ( 1/2 ) - 1 * log( 1 ) = 1；   可以看到，分类之后熵反而增大了

② 第二种分法就是红球自己一组，剩下两个黑球一组：

在红球组中出现黑球的概率是0, 在黑球组中出现红球的概率是0, 这样的分类已经“纯”了，也就是分类后子集中的随机变量已经变成确定性的了；

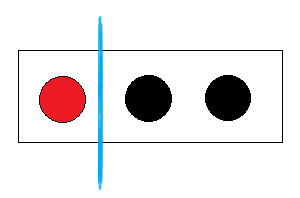
　　E(红|黑黑) = E(红) + E(黑黑) = - 1 * log( 1 ) - 1 * log( 1 ) = 0

决策树的目标

• 我们使用决策树模型的最终目的是利用决策树模型进行分类预测，预测我们给出的一组数据最终属于哪一种类别，这是一个由不确定到确定的过程；
• 最终理想的分类是，每一组数据，都能确定性地按照决策树分支找到对应的类别
• 所以我们就选择使数据信息熵下降最快的特征作为分类节点，使得决策树尽快地趋于确定

条件熵（conditional entropy）

条件熵 H( Y|X ) 表示在已知随机变量 X 的条件下随机变量 Y 的不确定性：

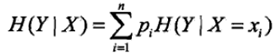    其中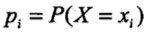

• 熵 H(D) 表示对数据集 D 进行分类的不确定性。
• 条件熵 H(D|A) 指在给定特征 A 的条件下数据集分类的不确定性
• 当熵和条件熵的概率由数据估计得到时，所对应的熵与条件熵分别称为经验熵（empirical entropy）和经验条件熵（empirical conditional entropy）

信息增益

特征A对训练数据集D的信息增益 g(D, A)，定义为集合D的经验熵H(D)与特征A给定条件下D的条件熵 H(D|A)之差，即

• 决策树学习应用信息增益准则选择特征
• 经验熵H(D)表示对数据集D进行分类的不确定性。而经验条件熵H(D|A)表示在特征A给定的条件下对数据集D进行分类的不确定性。那么它们的差，即信息增益，就表示由于特征A而使得对数据集D的分类的不确定性减少的程度
• 对于数据集D而言，信息增益依赖于特征，不同的特征往往具有不同的信息增益
• 信息增益大的特征具有更强的分类能力

决策树的生成算法

决策树（ID3）的训练过程就是找到信息增益最大的特征，然后按照此特征进行分类，然后再找到各类型子集中信息增益最大的特征，然后按照此特征进行分类，最终得到符合要求的模型；
C4.5算法在ID3基础上做了改进，用信息增益比来选择特征；
分类与回归树（CART）：  由特征选择、树的生成和剪枝三部分组成，既可以用于分类也可以用于回归；