CodeForces-1265E（期望）

题意

有1~n镜子，每个镜子说你漂亮的概率是pi/100，如果第i个回答你漂亮那么就一直问到第n个说漂亮为止，否则重新从1开始问，一天只问一个镜子，问直到镜子n说你漂亮的期望天数。

思路

设Ei为问到第i个镜子直到第n个成功的期望天数。

看以下推导：

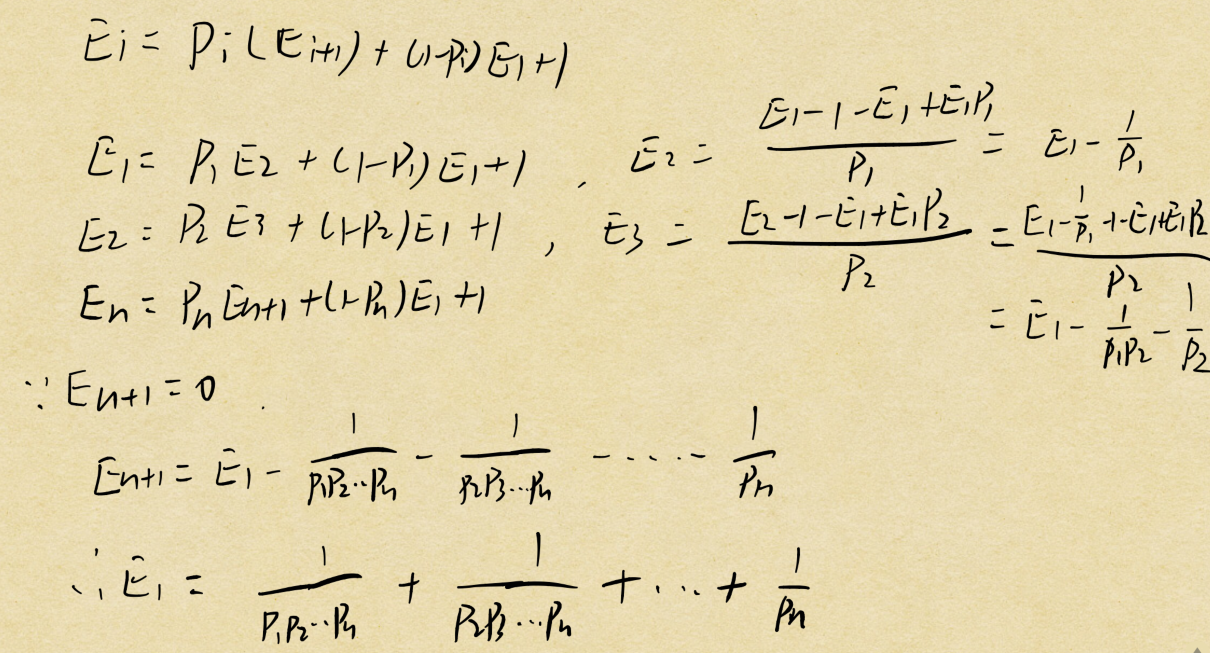
代码

#include<bits/stdc++.h>
using namespace std;
#define inf 0x3f3f3f3f
#define ll long long
const int N=200005;
const int mod=998244353;
const double eps=1e-8;
const double PI = acos(-1.0);
#define lowbit(x) (x&(-x))
ll gcd(ll a,ll b){return b==0?a:gcd(b,a%b);}
ll qpow(ll a,ll b){ll res=1;while(b){if(b&1) res=res*a%mod;a=a*a%mod;b>>=1;}return res;}
ll inv(ll a,ll p){return qpow(a,p-2);}
ll read()
{
   ll x=0;
   char ch=getchar();
   while(!isdigit(ch))
   {
       ch=getchar();
   }
   while(isdigit(ch))
   {
        x=x*10+(ch-'0');
        ch=getchar();
   }
   return x;
}
ll p[N];
int main()
{
    std::ios::sync_with_stdio(false);
    ll n=read(),sum=0,tmp=1;
    for(int i=1;i<=n;i++)
    {
        p[i]=read();
    }
    for(int i=n;i>=1;i--)
    {
        tmp=inv(p[i]*inv(100,mod)%mod,mod)*tmp%mod;
        sum=(sum+tmp)%mod;
    }
    cout<<sum<<endl;
    return 0;
}