[Python] 常见的排序与搜索算法
说明：
本文主要使用python实现常见的排序与搜索算法：冒泡排序、选择排序、插入排序、希尔排序、快速排序、归并排序以及二分查找等。
对算法的基本思想作简要说明，只要理解了基本的思想，与实现语言无关。
本文主要参考网络文章，仅供学习。
开发环境：Python3.5
一、冒泡排序
冒泡排序（Bubble Sort）算是一种比较常见的排序算法，重复遍历要排序的数列，一次比较相邻的两个元素，如果顺序错误即互相交换位置，遍历直到无需再交换，则此时数列已经排序完成。此算法名字由来：因为越小的元素（升序）经由交换慢慢 “浮”到数列的顶端。
1、冒泡排序的基本思想（运作原理）：
· 比较相邻的元素，如果第一个比第二个大（升序），就交换它们两个。
· 对每一对相邻的元素作同样的工作，从开始第一对到结尾最后一对，这一步做完后，最后的元素会是最大的数。
· 针对所有的元素重复以上的步骤，除了最后一个（倒数第二个与其已作比较）。
· 持续每次对越来越少的元素重复上面的步骤，知道没有任何一对数字需要比较。
交换过程示意图（第一次）（来自网络）：
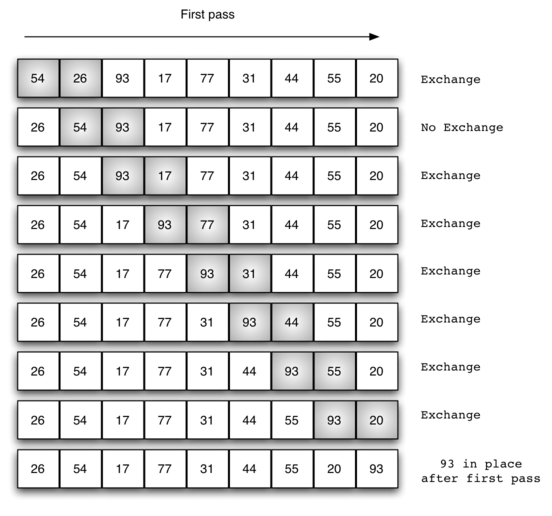
2、python实现过程：
这里提供两种实现过程，第二个实现过程为上面示意图所示。
# coding=utf-8 def bubble_sort(ls):
"""冒泡排序"""
print("before: ", ls)
for i in range(0, len(ls) - 1):
# i = [0, 1, ...., len(ls) - 2]，每次比较的第一个数的下标
# j = [i + 1, i + 2, ..., len(ls) - 1]，每次比较的第二个数的下标
for j in range(i + 1, len(ls)):
if ls[i] > ls[j]:
ls[i], ls[j] = ls[j], ls[i]
print(ls)
print("after: ", ls) def bubble_sort2(ls):
"""冒泡排序"""
print("before：", ls)
for j in range(len(ls) - 1, 0, -1):
# j = [len(ls) - 1, len(ls) - 2, ..., 1], 每次需要比较的次数
# i = [0, 1, 2, ..., j - 1]，需要比较的下标
for i in range(j):
if ls[i] > ls[i + 1]:
ls[i], ls[i + 1] = ls[i + 1], ls[i]
print(ls)
print("after：", ls) if __name__ == "__main__":
ls1 = [54, 26, 93, 17, 77, 31, 44, 55, 20]
ls2 = [54, 26, 93, 17, 77, 31, 44, 55, 20] bubble_sort(ls1)
print("-"*50)
bubble_sort2(ls2)
执行结果（分割线上为 bubble_sort1() 的执行结果，分割线下为 bubble_sort2() 的执行结果）：
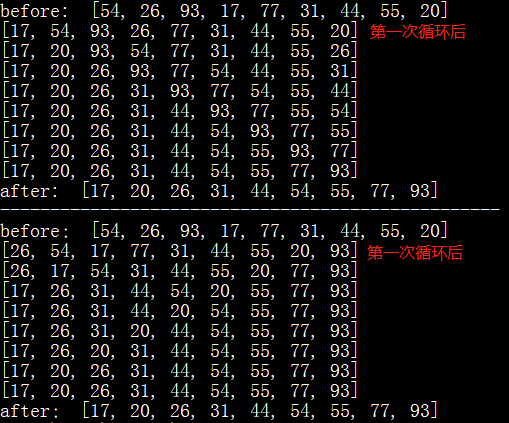
3、时间复杂度：
最优时间复杂度：O(n)（表示遍历一次发现没有任何可以交换的元素排序结束，在内循环可以做一个标识判断，如果首次循环没有任何交换，则跳出）
最坏复杂度：O(n2)
稳定性：稳定
二、选择排序
选择排序（ Selection Sort ）是一种简单直观的排序算法，基本原理：首先在未排序中找到最小（大）的元素，存放在排序序列的起始位置，然后在从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序的末尾，一次类推，直到所有元素均排序完毕。
选择排序的主要优点与数据移动有关。如果某个元素位于正确的最终位置上，则它不会被移动。选择排序每次交换一对元素，它们当中至少有一个呗移到其最终位置上，因此对 n 个元素的表进行排序共进行至多 n - 1次交换。在所有完成依靠交换去移动元素的排序方法中，选择排序属于非常好的一种。
1、排序过程，图示（图来源网络）：
假设右边为已排序，然后从左边未排序中选择一个最大值，放到右边来。
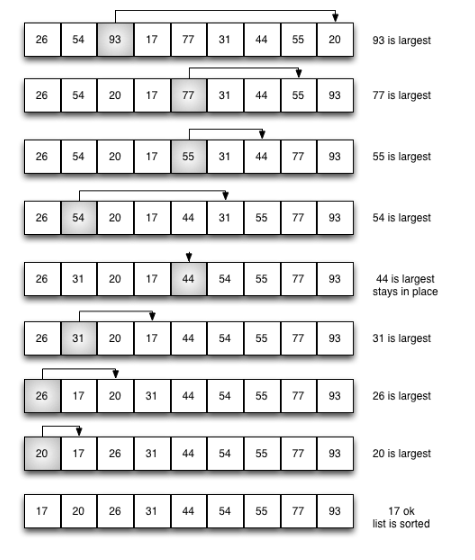
2、python实现过程：
这里代码的思想为：假设左边为已排序，右边为排序。
# coding=utf-8 def selection_sort(ls):
"""选择排序"""
# 假设左边为已排序，右边为未排序 print("before：", ls)
for i in range(0, len(ls) - 1):
# i = [0, 1, 2,,, len(ls) - 2]
# j = [i + 1, i + 2,,, len(ls) - 1]
min_index = i
for j in range(i + 1, len(ls)):
if ls[j] < ls[min_index]:
min_index = j if min_index != i:
ls[min_index], ls[i] = ls[i], ls[min_index]
print(ls)
print("after：", ls) if __name__ == "__main__":
ls = [54, 26, 93, 17, 77, 31, 44, 55, 20] selection_sort(ls)
3、时间复杂度：
最优时间复杂度：O(n2)
最坏时间复杂度：O(n2)
稳定性：不稳定（考虑升序每次选择最大的情况）
三、插入排序
插入排序（Insert ion Sort），其工作原理：通过构建有序序列，对于未排序数据中从后向前扫描，找到相应位置并插入。插入排序在实现上，在从后面向前扫描过程中，需要反复把已排序元素逐步向后挪位，为最新元素提供插入空间。
1、排序过程，图示意（图片来自网络）：
2、python实现过程：
从小标为 1 开始，往 0 遍历，比较交换。
# coding=utf-8 def insert_sort(ls):
"""插入排序"""
# 假设左边已排序，右边为未排序，每次从右边取一个数，遍历已排序的子序列，直到找到次数的位置。
print("before: ", ls)
for j in range(1, len(ls)):
for i in range(j, 0, - 1):
if ls[i] < ls[i - 1]:
ls[i], ls[i - 1] = ls[i - 1], ls[i]
print(ls)
print("after: ", ls) if __name__ == "__main__":
ls = [54, 26, 93, 17, 77, 31, 44, 55, 20] insert_sort(ls)
执行结果：
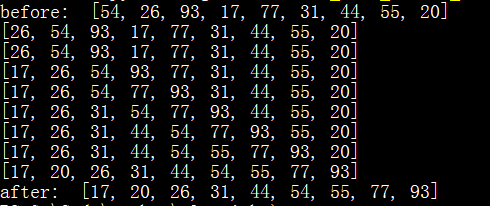
3、时间复杂度：
最优时间复杂度：O(n)（升序序列，序列已经处于升序状态）
最坏时间复杂度：O(n2)
稳定性：稳定
四、希尔排序
希尔排序（Shell Sort）是插入排序的一种。也称为增量排序，是直接插入排序算法的一种更高效的改进版本。希尔排序是把纪录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至 1 时，整个序列恰被分成一组，算法便终止。
1、希尔排序过程：
基本思想：将数组列在一个表中并对列分别进行插入排序，重复这过程，不过每次用更长的列（步长更长了，列数更少了）来进行。最后整个表就只有一列了。将数组转换至表识为了更好理解这算法，算法本身还是使用数组进行排序。
例如，假设有这样一组数[ 13 14 94 33 82 25 59 94 65 23 45 27 73 25 39 10 ]，如果我们以步长为5开始进行排序，我们可以通过将这列表放在有5列的表中进行更好的描述算法，这样它们就应该看起来是这样（竖着的元素是步长组成）：
最后以 1 步长进行排序（此时就是简单的插入排序）
2、python实现过程：
实现过程基本和插入排序类似，只是插入排序的 step 固定为 1，而希尔排序的 step 会变化直至 为 1。
# coding=utf-8 def shell_sort(ls):
"""希尔排序"""
print("before: ", ls) step = len(ls) // 2 # 初始步长 while step > 0:
# 插入排序
for j in range(step, len(ls)):
for i in range(j, 0, - step):
if ls[i] < ls[i - step]:
ls[i], ls[i - step] = ls[i - step], ls[i]
step //= 2
print(ls)
print("shell_sort ：", ls) if __name__ == "__main__":
ls = [54, 26, 93, 17, 77, 31, 44, 55, 20] shell_sort(ls)
执行结果：
3、时间复杂度：
最优时间复杂度：根据步长序列的不同而不同。
最坏时间复杂度：O(n2)。
稳定性：不稳定。
五、快速排序
快速排序（Quick Sort），又称为划分交换排序（Partition-exchange Sort），通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要笑，然后在按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。
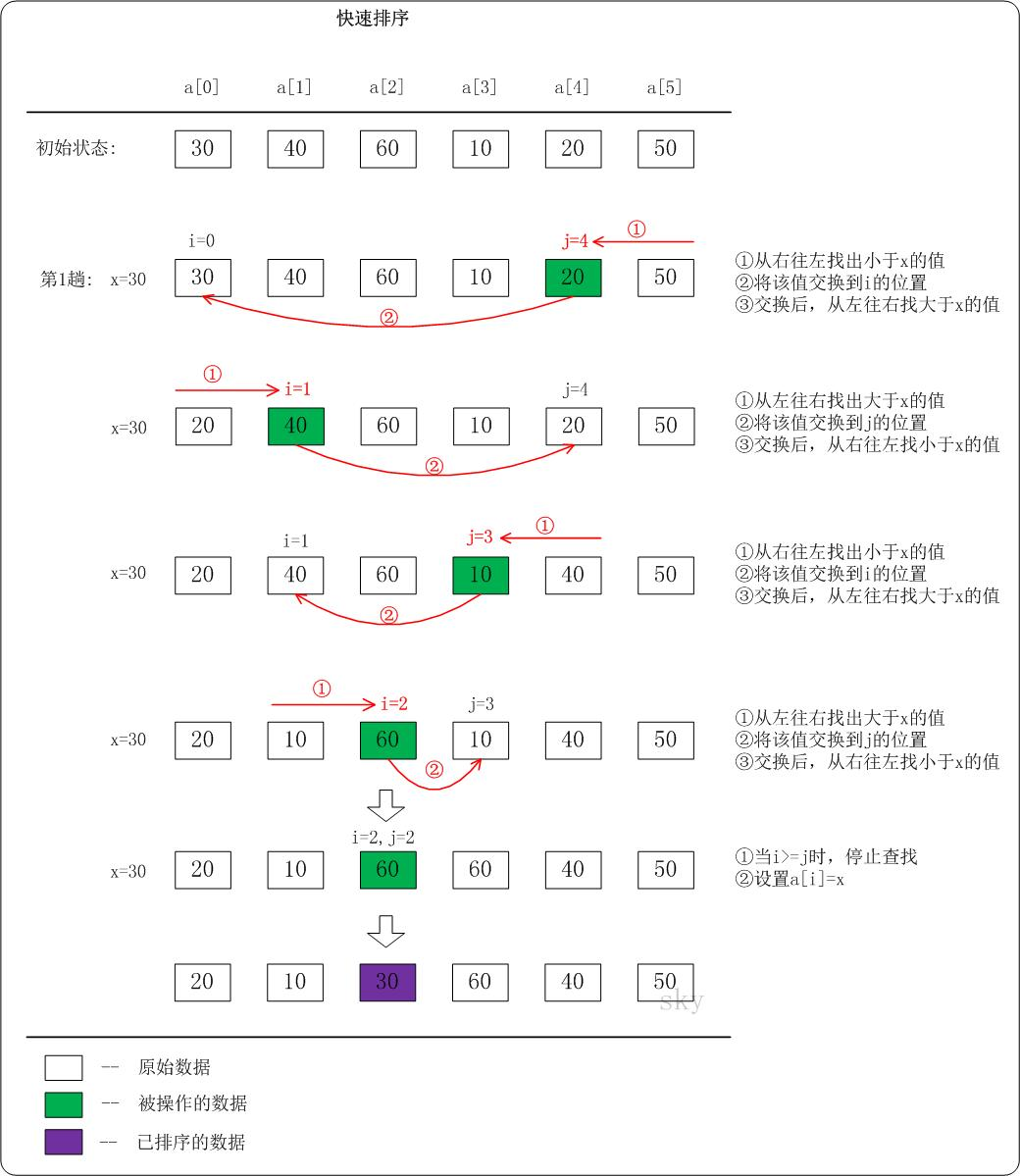
1、快速排序过程：
① 从数列中选出一个元素，称为“基准”（pivot）。
② 重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准大的摆在基准的后面（相同的数，可以放到任意一边）。在这个分区结束之后，该基准就处于数列的中间位置。这个称为分区（partition）操作。
③ 递归（recursive）把小于基准值元素子数列和大于基准值元素的子数列排序。
递归的的最底部情形，是数列的大小是零或一，也就是永远都已经被排序好了。
2、python实现过程：
这里提供两种快速排序的方式，基本思想一样，第一种是在原有列表进行操作（通过游标进行），第二种则是新建左右子列表进行存储。
# coding=utf-8 def quick_sort1(ls, start, end):
"""
快速排序-1
low 和 high 分别指向序列的头和尾
low += 1， high -= 1
在low自增过程中，直到找到大于 mid_val 的下标
在high自增减过程中，直到找到小于 mid_val 的小标
然后将这两个值交换
""" # 递归退出条件
if start >= end:
return low = start
high = end
mid_val = ls[low] while low < high:
while low < high and ls[high] > mid_val:
high -= 1
ls[low] = ls[high] while low < high and ls[low] < mid_val:
low += 1
ls[high] = ls[low] ls[low] = mid_val print("mid:", mid_val, ls) quick_sort1(ls, start, low - 1) # 左边的子序列
quick_sort1(ls, low + 1, end) # 右边的子序列 return ls def quick_sort2(ls):
"""快速排序-2""" # 递归退出条件
if len(ls) <= 1:
return ls left_ls, right_ls = [],[]
mid_val = ls[0]
for i in range(1, len(ls)):
if ls[i] < mid_val:
left_ls.append(ls[i])
else:
right_ls.append(ls[i]) print(left_ls, mid_val, right_ls) # 递归调用，左右子列表
left_res = quick_sort2(left_ls)
right_res = quick_sort2(right_ls) return left_res + [mid_val] + right_res if __name__ == "__main__":
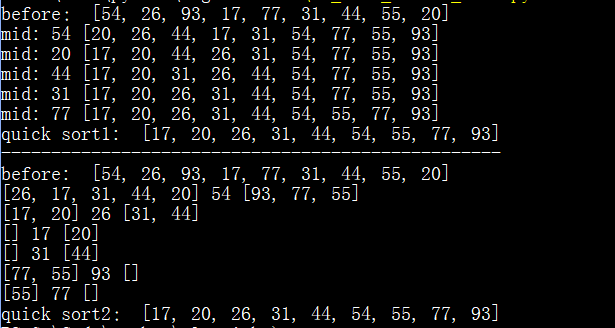
ls1 = [54, 26, 93, 17, 77, 31, 44, 55, 20]
ls2 = [54, 26, 93, 17, 77, 31, 44, 55, 20] print("before：", ls1)
res1 = quick_sort1(ls1, 0, len(ls1) - 1)
print("quick sort1: ", res1) print("-"*50)
print("before: ", ls2)
res2 = quick_sort2(ls2)
print("quick sort2：", res2)
执行结果：
3、时间复杂度：
最优时间复杂度：O(nlogn)
最坏时间复杂度：O(n2)
稳定性：不稳定
六、归并排序
归并排序是采用分治法的一种非常典型的应用。归并排序的思想就是先递归分解数组，再合并数组。
将数组分解最小之后，然后合并两个有序数组，基本思路：比较两个数组的最前面的数，谁小就先取谁，取了后相应的指针就往后移一位。然后再比较，直到一个数组为空，最后把另外一个数组的剩余部分复制过来即可。
1、归并排序过程，图示：
2、python实现过程：
先把序列拆分成 left_ls 和 right_ls ，然后再合并成一个res。
# coding=utf-8 def merge_sort(ls):
"""归并排序"""
n = len(ls) # 递归退出条件
if n <= 1:
return ls mid = n // 2 # 1、拆分子序列
left_ls = merge_sort(ls[:mid])
right_ls = merge_sort(ls[mid:]) # 2、合并子序列：left_ls 和 right_ls
left_point, right_point = 0, 0
res = [] # 当left_ls或者right_ls 结束，就会退出 while，而另外一个则可能未结束，所有后面需要 res +=
while left_point < len(left_ls) and right_point < len(right_ls):
# 比较两个子序列，小的先加入到 res[]
if left_ls[left_point] < right_ls[right_point]:
res.append(left_ls[left_point])
left_point += 1
else:
res.append(right_ls[right_point])
right_point += 1
print("res:", res) res += left_ls[left_point:]
res += right_ls[right_point:] return res if __name__ == "__main__":
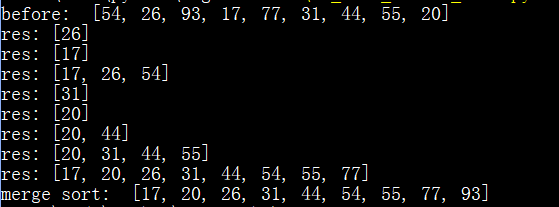
ls = [54, 26, 93, 17, 77, 31, 44, 55, 20] print("before: ", ls)
res = merge_sort(ls)
print("merge sort: ", res)
执行结果：
3、时间复杂度：
最优时间复杂度：O(nlogn)
最坏时间复杂度：O(nlogn)
稳定性：稳定
七、二分查找
二分查找又称折半查找，优点是比较次数少，查找速度快，平均性能好，其缺点是要求待查找表为有序表，且插入删除困难。因此，折半查找方法适用于不经常变动而查找频繁的有序列表。
基本思想：假设表中元素是按升序排序，将表中间位置记录关键字与查找关键字比较，如果两者相等，则查找成功，否则利用中间位置记录分成前、后两个子表，如果中间位置记录的关键字大于查找关键字，则进一步查找前一子表，否则进一步查找后一个子表。重复以上过程，知道找到满足条件的记录，使查找成功，或直到子表不存在为止，此时查找不成功。
1、二分查找过程，图示（图片来源网络）：
2、python实现过程：
这里主要两种实现方式，一种递归，另一种非递归。
# coding=utf-8 def binary_search_recursion(ls, item):
"""二分查找---递归"""
n = len(ls)
if n < 1:
return False mid = n // 2 # 与中间值比较
if item == ls[mid]:
return True # 去左边子序列查找
elif item < ls[mid]:
return binary_search_recursion(ls[:mid], item) # 去右边子序列查找
else:
return binary_search_recursion(ls[mid + 1:], item) def binary_search(ls, item):
"""二分查找---非递归"""
n = len(ls)
start = 0
end = n - 1 while start <= end:
mid = (start + end) // 2 if item == ls[mid]:
return True
elif item < ls[mid]:
end = mid - 1
else:
start = mid + 1
return False if __name__ == "__main__":
ls = [17, 20, 26, 31, 44, 54, 55, 77, 93] num = int(input("请输入一个整数:"))
res = binary_search(ls, num)
print("查找结果：", res)
八、完整代码
# coding=utf-8 def bubble_sort(ls):
"""冒泡排序"""
print("before: ", ls)
for i in range(0, len(ls) - 1):
# i = [0, 1, ...., len(ls) - 2]，每次比较的第一个数的下标
# j = [i + 1, i + 2, ..., len(ls) - 1]，每次比较的第二个数的下标
for j in range(i + 1, len(ls)):
if ls[i] > ls[j]:
ls[i], ls[j] = ls[j], ls[i]
print(ls)
print("after: ", ls) def bubble_sort2(ls):
"""冒泡排序"""
print("before：", ls)
for j in range(len(ls) - 1, 0, -1):
# j = [len(ls) - 1, len(ls) - 2, ..., 1], 每次需要比较的次数
# i = [0, 1, 2, ..., j - 1]，需要比较的下标
for i in range(j):
if ls[i] > ls[i + 1]:
ls[i], ls[i + 1] = ls[i + 1], ls[i]
print(ls)
print("after：", ls) def selection_sort(ls):
"""选择排序"""
# 假设左边为已排序，右边为未排序 print("before：", ls)
for i in range(0, len(ls) - 1):
# i = [0, 1, 2,,, len(ls) - 2]
# j = [i + 1, i + 2,,, len(ls) - 1]
min_index = i
for j in range(i + 1, len(ls)):
if ls[j] < ls[min_index]:
min_index = j if min_index != i:
ls[min_index], ls[i] = ls[i], ls[min_index]
print(ls)
print("after：", ls) def insert_sort(ls):
"""插入排序"""
# 假设左边已排序，右边为未排序，每次从右边取一个数，遍历已排序的子序列，直到找到次数的位置。
print("before: ", ls)
for j in range(1, len(ls)):
for i in range(j, 0, - 1):
if ls[i] < ls[i - 1]:
ls[i], ls[i - 1] = ls[i - 1], ls[i]
print(ls)
print("after: ", ls) def shell_sort(ls):
"""希尔排序"""
print("before: ", ls) step = len(ls) // 2 # 初始步长 while step > 0:
# 插入排序
for j in range(step, len(ls)):
for i in range(j, 0, - step):
if ls[i] < ls[i - step]:
ls[i], ls[i - step] = ls[i - step], ls[i]
step //= 2
print(ls)
print("shell_sort ：", ls) def quick_sort1(ls, start, end):
"""
快速排序-1
low 和 high 分别指向序列的头和尾
low += 1， high -= 1
在low自增过程中，直到找到大于 mid_val 的下标
在high自增减过程中，直到找到小于 mid_val 的小标
然后将这两个值交换
""" # 递归退出条件
if start >= end:
return low = start
high = end
mid_val = ls[low] while low < high:
while low < high and ls[high] > mid_val:
high -= 1
ls[low] = ls[high] while low < high and ls[low] < mid_val:
low += 1
ls[high] = ls[low] ls[low] = mid_val print("mid:", mid_val, ls) quick_sort1(ls, start, low - 1) # 左边的子序列
quick_sort1(ls, low + 1, end) # 右边的子序列 return ls def quick_sort2(ls):
"""快速排序-2""" # 递归退出条件
if len(ls) <= 1:
return ls left_ls, right_ls = [],[]
mid_val = ls[0]
for i in range(1, len(ls)):
if ls[i] < mid_val:
left_ls.append(ls[i])
else:
right_ls.append(ls[i]) print(left_ls, mid_val, right_ls) # 递归调用，左右子列表
left_res = quick_sort2(left_ls)
right_res = quick_sort2(right_ls) return left_res + [mid_val] + right_res def merge_sort(ls):
"""归并排序"""
n = len(ls) # 递归退出条件
if n <= 1:
return ls mid = n // 2 # 1、拆分子序列
left_ls = merge_sort(ls[:mid])
right_ls = merge_sort(ls[mid:]) # 2、合并子序列：left_ls 和 right_ls
left_point, right_point = 0, 0
res = [] # 当left_ls或者right_ls 结束，就会退出 while，而另外一个则可能未结束，所有后面需要 res +=
while left_point < len(left_ls) and right_point < len(right_ls):
# 比较两个子序列，小的先加入到 res[]
if left_ls[left_point] < right_ls[right_point]:
res.append(left_ls[left_point])
left_point += 1
else:
res.append(right_ls[right_point])
right_point += 1
print("res:", res) res += left_ls[left_point:]
res += right_ls[right_point:] return res def binary_search_recursion(ls, item):
"""二分查找---递归"""
n = len(ls)
if n < 1:
return False mid = n // 2 # 与中间值比较
if item == ls[mid]:
return True # 去左边子序列查找
elif item < ls[mid]:
return binary_search_recursion(ls[:mid], item) # 去右边子序列查找
else:
return binary_search_recursion(ls[mid + 1:], item) def binary_search(ls, item):
"""二分查找---非递归"""
n = len(ls)
start = 0
end = n - 1 while start <= end:
mid = (start + end) // 2 if item == ls[mid]:
return True
elif item < ls[mid]:
end = mid - 1
else:
start = mid + 1
return False
排序与查找算法.py
[Python] 常见的排序与搜索算法的更多相关文章
- 为什么我要放弃javaScript数据结构与算法（第十章）—— 排序和搜索算法
本章将会学习最常见的排序和搜索算法,如冒泡排序.选择排序.插入排序.归并排序.快速排序和堆排序,以及顺序排序和二叉搜索算法. 第十章 排序和搜索算法 排序算法 我们会从一个最慢的开始,接着是一些性能好 ...
- python常见排序算法解析
python——常见排序算法解析 算法是程序员的灵魂. 下面的博文是我整理的感觉还不错的算法实现 原理的理解是最重要的,我会常回来看看,并坚持每天刷leetcode 本篇主要实现九(八)大排序算法 ...
- Python全栈开发之5、几种常见的排序算法以及collections模块提供的数据结构
转载请注明出处http://www.cnblogs.com/Wxtrkbc/p/5492298.html 在面试中,经常会遇到一些考排序算法的题,在这里,我就简单了列举了几种最常见的排序算法供大家学习 ...
- 几种常见的排序方法总结（Python）
几种常见的排序算法总结(Python) 排序算法:是一种能将一串数据依照特定顺序进行排序的一种算法. 稳定性:稳定排序算法会让原本有相等键值的记录维持相对次序.也就是如果一个排序算法是稳定的,当有两个 ...
- Python常见的错误汇总
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++ 错误: [错误分析]第二个参数必须为类,否则会报TypeError,所以正确的应 ...
- 【Python】常用排序算法的python实现和性能分析
作者:waterxi 原文链接 背景 一年一度的换工作高峰又到了,HR大概每天都塞几份简历过来,基本上一天安排两个面试的话,当天就只能加班干活了.趁着面试别人的机会,自己也把一些基础算法和一些面试题整 ...
- 用 python 实现各种排序算法-乾颐堂
总结了一下常见集中排序的算法 归并排序 归并排序也称合并排序,是分治法的典型应用.分治思想是将每个问题分解成个个小问题,将每个小问题解决,然后合并. 具体的归并排序就是,将一组无序数按n/2递归分解成 ...
- Python应用——自定义排序全套方案
本文始发于个人公众号:TechFlow,原创不易,求个关注 今天的这篇文章和大家聊聊Python当中的排序,和很多高级语言一样,Python封装了成熟的排序函数.我们只需要调用内部的sort函数,就可 ...
- python3实现几种常见的排序算法
python3实现几种常见的排序算法 冒泡排序 冒泡排序是一种简单的排序算法.它重复地走访过要排序的数列,一次比较两个元素,如果它们的顺序错误就把它们交换过来.走访数列的工作是重复地进行直到没有再需要 ...
随机推荐
- JAVA面试题 String s = new String("xyz");产生了几个对象？
面试官Q1:请问String s = new String("xyz");产生了几个对象? 对于这个Java面试题,老套路先上代码: public class StringTest ...
- d3.js实现柱形图，饼图以及折现图
饼图 var width = 500; var height = 500; //处理数据 var dataset = [ 30 , 10 , 43 , 55 , 13 ]; var pie = d3. ...
- Spring源码分析之环境搭建
写在最前面 最近突然心血来潮,想看看源码,看看大牛都怎么码代码,膜拜下.首选肯定是spring大法,于是说干就干,从GitHub上下载spring-framework源码编译拜读. 环境搭建 安装JD ...
- 【pycharm】Pycharm对 axios语法的支持问题
问题: 解决办法: 1,找到pychar的settings 2,ECMAScript6
- Java经典编程题
[程序1] 题目:古典问题:有一对兔子,从出生后第3个月起每个月都生一对兔子,小兔子长到第三个月后每个月又生一对兔子,假如兔子都不死,问每个月的兔子总数为多少? //这是一个菲波拉契数列问题p ...
- Hadoop学习(5)-zookeeper的安装和命令行，java操作
zookeeper是干嘛的呢 Zookeeper的作用1.可以为客户端管理少量的数据kvkey:是以路径的形式表示的,那就意味着,各key之间有父子关系,比如/ 是顶层key用户建的key只能在/ 下 ...
- 2、大型项目的接口自动化实践记录--接口测试简介及RequestsLibrary关键字简介
1.接口测试简介 1)先简单介绍下接口测试,那么什么是接口测试呢? 百科的回答:接口测试是测试系统组件间接口的一种测试.接口测试主要用于检测外部系统与系统之间以及内部各个子系统之间的交互点. 看起来有 ...
- 【转】C++文件读写详解（ofstream,ifstream,fstream）
转:http://blog.csdn.net/kingstar158/article/details/6859379 摘要:具体用法,上面链接中,文章写的很详细,讲解ofstream,ifstream ...
- Element UI系列：Select下拉框实现默认选择
实现的主要关键点在于 v-mode 所绑定的值,必须是 options 数组中对应的 value 值
- 变量Variable
变量Variable 内存 #conding:utf-8 a = 1 #conding:utf-8 a = 1 b = a #conding:utf-8 a = 1 b = a a = 2 命名规则 ...