第三篇视觉里程计（VO）的初始化过程以及openvslam中的相关实现详解

视觉里程计（Visual Odometry, VO），通过使用相机提供的连续帧图像信息（以及局部地图，先不考虑）来估计相邻帧的相机运动，将这些相对运行转换为以第一帧为参考的位姿信息，就得到了相机载体（假设统一的刚体）的里程信息。先上一张本文主要内容的框图：

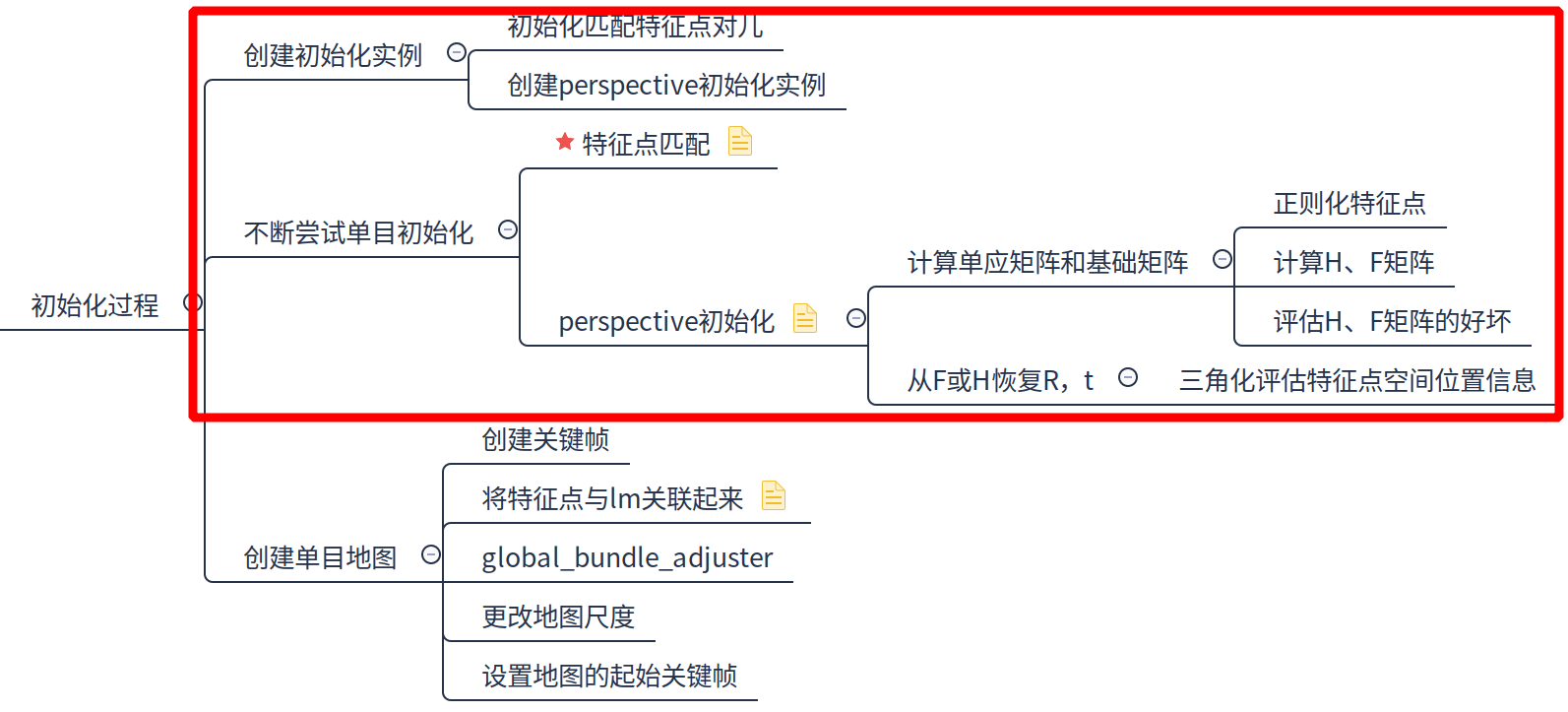
初始化实例

在实例化跟踪器的时候会实例化一个初始化实例，有一些比较重要的参数需要注意下，看代码注释以及初始值，参数值也可以在yaml文件中自定义。

// src/openvslam/module/initializer.h:83

//! max number of iterations of RANSAC (only for monocular initializer)

const unsigned int num_ransac_iters_;

//! min number of triangulated pts

const unsigned int min_num_triangulated_;

//! min parallax (only for monocular initializer)

const float parallax_deg_thr_;

//! reprojection error threshold (only for monocular initializer)

const float reproj_err_thr_;

//! max number of iterations of BA (only for monocular initializer)

const unsigned int num_ba_iters_;

//! initial scaling factor (only for monocular initializer)

const float scaling_factor_;

// src/openvslam/module/initializer.cc:16

initializer::initializer(const camera::setup_type_t setup_type,

                         data::map_database* map_db, data::bow_database* bow_db,

                         const YAML::Node& yaml_node)

        : setup_type_(setup_type), map_db_(map_db), bow_db_(bow_db),

          num_ransac_iters_(yaml_node["Initializer.num_ransac_iterations"].as<unsigned int>(100)),

          min_num_triangulated_(yaml_node["Initializer.num_min_triangulated_pts"].as<unsigned int>(50)),

          parallax_deg_thr_(yaml_node["Initializer.parallax_deg_threshold"].as<float>(1.0)),

          reproj_err_thr_(yaml_node["Initializer.reprojection_error_threshold"].as<float>(4.0)),

          num_ba_iters_(yaml_node["Initializer.num_ba_iterations"].as<unsigned int>(20)),

          scaling_factor_(yaml_node["Initializer.scaling_factor"].as<float>(1.0)) {

    spdlog::debug("CONSTRUCT: module::initializer");

}

使用不同的相机类型，初始化的方法也不相同，openvslam使用了perspective和bearing_vector两种初始化方法。

// src/openvslam/module/initializer.cc:91

void initializer::create_initializer(data::frame& curr_frm) {

    // 将当前帧设置为初始化过程中的参考帧

    init_frm_ = data::frame(curr_frm);

    // 将当前帧的特征点当作previously matched coordinates

    prev_matched_coords_.resize(init_frm_.undist_keypts_.size());

    for (unsigned int i = 0; i < init_frm_.undist_keypts_.size(); ++i) {

        prev_matched_coords_.at(i) = init_frm_.undist_keypts_.at(i).pt;

    }

    // initialize matchings (init_idx -> curr_idx)

    std::fill(init_matches_.begin(), init_matches_.end(), -1);

    // build a initializer

    initializer_.reset(nullptr);

    switch (init_frm_.camera_->model_type_) {

        case camera::model_type_t::Perspective:

        case camera::model_type_t::Fisheye: {

            initializer_ = std::unique_ptr<initialize::perspective>(new initialize::perspective(init_frm_,

                                                                                                num_ransac_iters_, min_num_triangulated_,

                                                                                                parallax_deg_thr_, reproj_err_thr_));

            break;

        }

        case camera::model_type_t::Equirectangular: {

            initializer_ = std::unique_ptr<initialize::bearing_vector>(new initialize::bearing_vector(init_frm_,

                                                                                                      num_ransac_iters_,            min_num_triangulated_,

                                                                                                      parallax_deg_thr_, reproj_err_thr_));

            break;

        }

    }

    // 设置状态为初始化状态

    state_ = initializer_state_t::Initializing;

}

执行完上面的函数后回直接直接退出，然后读取下一帧图像，进入初始化阶段。下面的匹配过程，在上一篇已经详细讲过了，有一点需要注意在匹配完成后，会将匹配到的点的prev_matched_coords_改为当前帧的特征点座标。如果匹配到的点数小于min_num_triangulated_（这里是50），则直接重置初始化，会把下一帧当作初始化的参考帧。

bool initializer::try_initialize_for_monocular(data::frame& curr_frm) {

    assert(state_ == initializer_state_t::Initializing);

    match::area matcher(0.9, true);

    const auto num_matches = matcher.match_in_consistent_area(init_frm_, curr_frm, prev_matched_coords_, init_matches_, 100);

    if (num_matches < min_num_triangulated_) {

        // rebuild the initializer with the next frame

        reset();

        return false;

    }

    // try to initialize with the current frame

    assert(initializer_);

    return initializer_->initialize(curr_frm, init_matches_);

}

初始化过程

通过计算单应矩阵和基础矩阵，评估出两帧之间的变换矩阵。首先搞清楚几个基本概念。

基础(Fundamental)矩阵

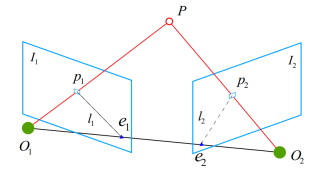
假设$I1$与$I2$为相邻帧，$p1$与$p2$为相邻帧匹配到的特征点，P为特征点的空间位置。対极约束描述了图像中特征点位置与帧间运动信息之间的关系。用过几何计算我们可以得到如下公式（对极约束）。具体推导可以参考两视图对极约束-基础矩阵：

\[p_2^TK^{-T}t^{\wedge }RK^{-1}p_1=0
\]

定义本质矩阵$E=t^{\wedge }R$，基础矩阵$F=K^{-T}EK$。通过匹配点对儿的像素位置可以计算出$E或F$，进而计算出$R,t$。

此外，假设相邻相机只做了旋转运动，即t为0，可以看到対极约束对于任意R都成立，因此想要通过对极约束评估相机运动内在要求不能只是纯旋转运动（可以使用单应矩阵来求解）。

单应Homography

单应(Homography)是射影几何中的概念，又称为射影变换。它把一个射影平面上的点(三维齐次矢量)映射到另一个射影平面上，并且把直线映射为直线，具有保线性质。总的来说，单应是关于三维齐次矢量的一种线性变换，可以用一个3×3的非奇异矩阵$H$表示:

\[\begin{pmatrix}u_1\\ v_1\\ 1\end{pmatrix}=
\begin{pmatrix}h_{11} & h_{12} & h_{13}\\h_{21} & h_{22} & h_{23}\\ h_{31} & h_{32} & h_{33}\end{pmatrix}
\begin{pmatrix}u_2\\ v_2\\ 1\end{pmatrix}
\]

其中，$(u1,v1,1)^T$表示图像1中的像点，$(u2,v2,1)^T$是图像2中的像点，也就是可以通过单应矩阵H将图像2变换到图像1，描述的是两个平面之间的映射关系。

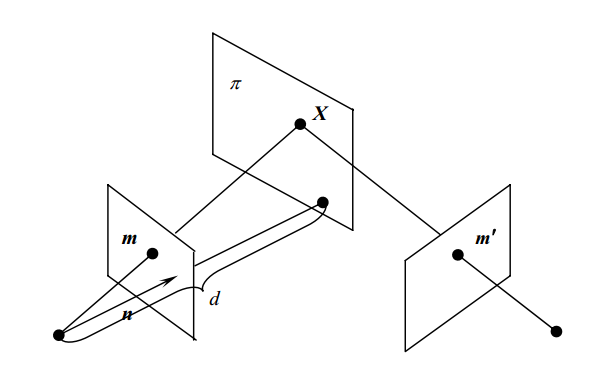
上图表示场景中的平面$π$在两相机的成像，设平面$π$在第一个相机坐标系下的单位法向量为$n^T$，其到第一个相机中心（坐标原点）的距离为$d$，则平面$π$可表示为：

\[n^TX_1=d
\]

其中，$X_1$是三维点P在第一相机坐标系下的坐标，其在第二个相机坐标系下的坐标为$X_2$，则

\[X_2 = RX_1 + t \\
X_2 = RX_1 + t\frac{1}{d}n^TX_1=(R+t\frac{1}{d}n^T)X_1=HX_1 \\
H = R+t\frac{1}{d}n^T\]

假设$p_1,p_2$为$X_1,X_2$对应的图像上的点，则

\[X_1=K^{-1}p_1, X_2=K^{-2}p_1\\
H = K(R+t\frac{1}{d}n^T)K^{-1}\]

这样求解出$H$便可以求解出$R,t$，并却$t=0$也不影响求解R。

实践

在实际中，通常会同时计算H和F。

\\ src/openvslam/initialize/perspective.cc:27

bool perspective::initialize(const data::frame& cur_frm, const std::vector<int>& ref_matches_with_cur)

{

    ...

    // compute H and F matrices

    auto homography_solver = solve::homography_solver(ref_undist_keypts_, cur_undist_keypts_, ref_cur_matches_, 1.0);

    auto fundamental_solver = solve::fundamental_solver(ref_undist_keypts_, cur_undist_keypts_, ref_cur_matches_, 1.0);

    std::thread thread_for_H(&solve::homography_solver::find_via_ransac, &homography_solver, num_ransac_iters_, true);

    std::thread thread_for_F(&solve::fundamental_solver::find_via_ransac, &fundamental_solver, num_ransac_iters_, true);

    thread_for_H.join();

    thread_for_F.join();

    ...

}

初始化

    使用两个线程分别计算H和F矩阵

        homography_solver::find_via_ransac

        fundamental_solver::find_via_ransac

    通过判断0.4<rel_score_H = score_H / (score_H + score_F来决定用H还是F来评估R，t，

    在评估的过程中还会通过三角化确定特征点的空间位置信息

    通过一些列复杂的筛选得出到满足条件的R，t即算完成初始化

看完下面的文章再回过头来看这段话。总的来说初始化过程涉及到多视几何的基础内容很多，openvlsam的实现很大程度上都是借鉴ORB2的实现方法（三角化除外）。可以看到由于要求前后帧（可以中间隔若干帧）特征点有一定的视差，想要成功的初始化就一定要发生位移。由于同时评估H和F矩阵，纯旋转也有初始化成功的可能性，但是需要有比较多的特征点在相同的平面上。不过最好还是就有旋转又有平移吧。这里在评估过程中都是采用归一化平面上的特征点（没有深度信息），所以得到的t是不知道其物理尺度的，然后三角化又是基于R，t求解的，因此特征点的空间位置值，也是无法知道其物理尺度的，可以认为尺度和t一致。

homography_solver::find_via_ransac

首先正则化特征点，目的是为了后面使用RANSAC（就是随即从大样本集抽取小样本集用于求解问题的方法）计算SVD时得到更一致的解决，消除特征点在图像中位置分布对结果的影响。更详细的解释可参考《Multiple View Geometry in Computer Vision 》P104 “4.4 Transformation invariance and normalization”。

openvslam采样的方法略有不同，分析如下。

\\src/openvslam/solve/common.cc:6

void normalize(const std::vector<cv::KeyPoint>& keypts, std::vector<cv::Point2f>& normalized_pts, Mat33_t& transform) {

计算单应矩阵

    正则化特征点

    循环num_ransac_iters_=100次

        生成8个点的RANSAC序列

        计算正则化特征点的单应矩阵compute_H_21

        计算特征点的单应矩阵

        评估当前求解出单应矩阵的好坏，更新最好的结果

    将筛选过的好的点重新评估H矩阵，得到最优结果

正则化特征点

正则化的公式如下，还是比较直观的。

\[x_i^{\prime} = {x_i - \bar{x} \over \sigma_x},y_i^{\prime} = {y_i - \bar{y} \over \sigma_y} \\
\bar{x} = {\Sigma{x_i} \over N},\bar{y} = {\Sigma{y_i} \over N} \\
\sigma_x = {\Sigma{\left|x_i - \bar{x}\right|} \over N}, \sigma_y = {\Sigma{\left|y_i - \bar{y}\right|} \over N} \\
\begin{pmatrix}x_i^{\prime} \\ y_i^{\prime} \\ 1\end{pmatrix}=
\begin{pmatrix}1/\sigma_x & 0 & -\frac{\bar{x}}{\sigma_x} \\ 0 & 1/\sigma_y & -\frac{\bar{y}}{\sigma_y} \\ 0 & 0 & 1\end{pmatrix}
\begin{pmatrix}x \\ y \\ 1\end{pmatrix}=T\begin{pmatrix}x \\ y \\ 1\end{pmatrix}\]

$x_i^{\prime},y_i^{\prime}$为正则化后的座标值，T就是正则化矩阵。

compute_H_21

参考https://www.uio.no/studier/emner/matnat/its/UNIK4690/v16/forelesninger/lecture_4_3-estimating-homographies-from-feature-correspondences.pdf

计算特征点的单应矩阵

程序中normalized_H_21表示则正则化的参考帧到当前帧的单应矩阵。

H_21_in_sac: 帧1->帧2的homography，注意21表示的是1->2。

\[p^{\prime}_{cur} = T_{cur}p_{cur} \\
p^{\prime}_{ref} = T_{ref}p_{ref} \\
\]

$T_{cur},T_{ref}$是当前帧特征点和参考帧特征点的正则化矩阵。

\[p^{\prime}_{cur}=H^{\prime}_{cr}p^{\prime}_{ref}
\]

$H^{\prime}_{rc}$是正则化当前帧特征点与正则化参考帧特征点的单应矩阵。展开得到:

\[T_{cur}p_{cur}=H^{\prime}_{cr}T_{ref}p_{ref} \\
p_{cur}=T^{-1}_{cur}H^{\prime}_{cr}T_{ref}p_{ref}
\]

因此当前帧特征点与参考帧特征点的单应矩阵$H_{cr}$为：

\[H_{cr}=T^{-1}_{cur}H^{\prime}_{cr}T_{ref}
\]

评估当前求解出单应矩阵的好坏

说实话，研究了半天也没搞清楚是如何和卡方检验联系起来的。在我看来就是定义了一个最小重投影误差门限（5.991），重投影误差小于门限就标记为inlier, 将最好的结果保存下来。这里面作者只累加小于门限的重投影误差，即score += 门限值 - 重投影误差，这个差值是>0的，这样做的好处大家可以思考下。

fundamental_solver::find_via_ransac

同样是先正则化特征点，然后采用RANSAC的方法计算F矩阵compute_F_21，过程和计算H矩阵完全一致。

从F或H恢复R，t

//src/openvslam/initialize/perspective.cc:91

bool perspective::reconstruct_with_H(const Mat33_t& H_ref_to_cur, const std::vector<bool>& is_inlier_match)

//src/openvslam/initialize/perspective.cc:114

bool perspective::reconstruct_with_F(const Mat33_t& F_ref_to_cur, const std::vector<bool>& is_inlier_match)

reconstruct_with_H: Motion and structure from motion in a piecewise planar environment (Faugeras et al. in IJPRAI 1988)

reconstruct_with_F: https://en.wikipedia.org/wiki/Essential_matrix#Determining_R_and_t_from_E

在得到若干组候选的R，t后，需要计算找到最佳的R，t。

// src/openvslam/initialize/base.cc:31

bool base::find_most_plausible_pose

寻找最佳位姿

    逐个候选位姿进行check_pose

    选取有效点最多的那组位姿，做以下判断：

    1.有效点数必须大于min_num_triangulated_（50）;

    2.一个好的结果应该是只有一组有比较多的有效点，，如果发现有很多组都有个数相近的有效点，则这些位姿都不对；

    3.视差不能太小，因为太小的视差评估出的深度不可靠，这里的门限parallax_deg_thr_=1度；

在评估R，t的同时会对特征点进行三角化，注意保存到triangulated_pts_的点是特征点在参考帧下的三维坐标。

check_pose

// src/openvslam/initialize/base.cc:86

unsigned int base::check_pose

循环所有的匹配点

    三角化计算得到特征点在参考帧下的三维坐标

    计算视差角的余弦值（向量内积的方法）

    排除视差小于0.5度和深度为负数的三维坐标

    验证特征点是否在参考帧和当前帧中可见，重投影误差L2 < 16

    以上条件都满足的点才认为有效

对视差排序后返回第50小或者（个数小于50则返回最小）的视差

Triangulate(三角化)

问题

评估H和F矩阵的好坏时是如何转为卡方检验的？

已解决，见 SLAM中的卡方分布。
triangulator::triangulate还没有彻底搞明白？