python算法与数据结构-队列(44)

一、队列的介绍

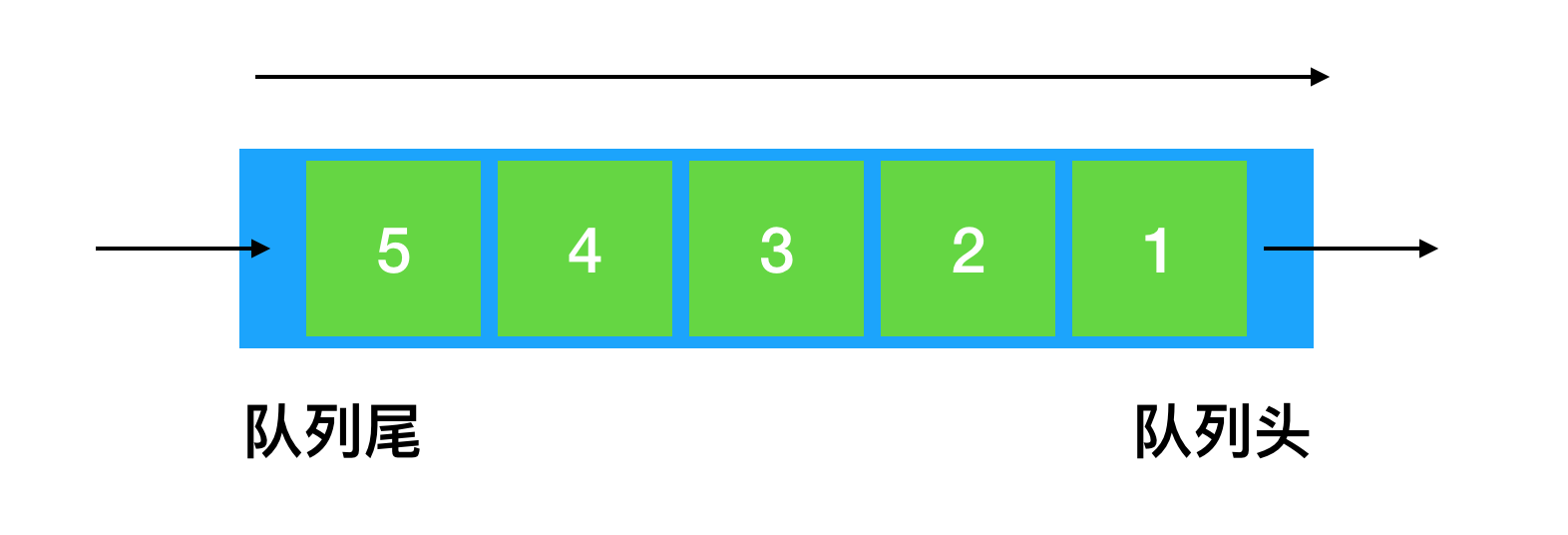
　　队列的定义：队列是一种特殊的线性表，只允许在表的头部（front处）进行删除操作，在表的尾部（rear处）进行插入操作的线性数据结构，这种结构就叫做队列。进行插入操作的一端称为队尾，进行删除操作的一端称为队尾。

　　队列的类型：链式队列，即用链表实现的队列。静态队列：即用数组实现的队列。

　　队列的特性：

• • 在队尾插入元素，在队首删除元素。
  • FIFO（先进先出），就向排队取票一样。

二、队列的python代码实现

class Queue(object):
    def __init__(self):
        print("===创建队列===")
        self.element = []
 
    def inQueue(self,num):
        self.element.append(num)
        print("%d进入队列"%num,end=" ")
 
    def is_empty(self):
        if len(self.element)==0:
            return True
        else:
            return False
 
    def outQueue(self):
        if self.is_empty()==True:
            print("你要删除的队列为空")
            return
        else:
            num = self.element[0]
            print("%d要出队列"%num,end=" ")
            self.element.pop(0)
 
    def length(self):
        return len(self.element)
 
    def travel(self):
        if self.is_empty()==True:
            print("你要遍历的队列为空")
            return
        else:
            print("你要遍历的队列元素有：",end=" ")
            for i in range(0,self.length()):
                print("%d "%self.element[i],end=" ")
            print("\n")
 
def main():
    q = Queue()
    print("===验证空队列===")
    q.travel()
    print("===往队列中添加数据===")
    q.inQueue(1)
    q.travel()
    q.inQueue(2)
    q.inQueue(3)
    q.inQueue(4)
    q.inQueue(5)
    q.travel()
    print("===验证出队列===")
    q.outQueue()
    q.travel()
    q.outQueue()
    q.travel()
 
if __name__ == '__main__':
    main()

运行结果为：

===创建队列===
===验证空队列===
你要遍历的队列为空
===往队列中添加数据===
1进入队列 你要遍历的队列元素有： 1  
 
2进入队列 3进入队列 4进入队列 5进入队列 你要遍历的队列元素有： 1  2  3  4  5  
 
===验证出队列===
1要出队列 你要遍历的队列元素有： 2  3  4  5  
 
2要出队列 你要遍历的队列元素有： 3  4  5  

三、队列的C语言代码实现

//  main.m
//  队列
//  Created by 侯垒 on 2019/7/3.
//  Copyright © 2019 可爱的侯老师. All rights reserved.
 
#include<stdio.h>
 
#define SIZE 20
typedef struct Q
{
    int array[SIZE];
    int front;
    int rear;
    int length;
}Queue;
 
void createQueue(Queue *q)
{
    q->front = ;
    q->rear = -;
    q->length = ;
    printf("创建队列成功\n");
}
 
void inQueue(Queue *q,int num)
{
    if (q->length >= SIZE)
    {
        printf("该队列已经满了\n");
    }
    else
    {
        q->rear = q->rear+;
        q->array[q->rear] = num;
        q->length++;
        printf("%d进入队列\n",num);
    }
}
 
void outQueue(Queue *q)
{
    if (q->length <= )
    {
        printf("这是一个空队列");
    }
    else
    {
        int num = q->array[q->front];
        printf("%d出队列 ",num);
        q->front = q->front+;
        q->length--;
    }
}
 
void travel(Queue *q)
{
    if (q->length <= )
    {
        printf("这是一个空队列\n");
    }
    else
    {
        printf("你遍历的队列里面的数据有：");
        for (int i=q->front; i<q->rear+; i++)
        {
            printf(" %d ",q->array[i]);
        }
        printf("\n");
    }
}
 
int main(int argc, const char * argv[]) {
 
    Queue q;
    createQueue(&q);
    travel(&q);
    inQueue(&q, );
    inQueue(&q, );
    inQueue(&q, );
    inQueue(&q, );
    inQueue(&q, );
    inQueue(&q, );
    travel(&q);
    outQueue(&q);
    travel(&q);
    outQueue(&q);
    travel(&q);
    outQueue(&q);
    travel(&q);
 
    return ;
}

运行结果为：

创建队列成功
这是一个空队列
1进入队列
2进入队列
3进入队列
4进入队列
5进入队列
6进入队列
你遍历的队列里面的数据有：
1出队列 你遍历的队列里面的数据有：
2出队列 你遍历的队列里面的数据有：
3出队列 你遍历的队列里面的数据有：      

四、双端队列

双端队列（deque，全名double-ended queue），是一种具有队列和栈的性质的数据结构。

双端队列中的元素可以从两端弹出，其限定插入和删除操作在表的两端进行。双端队列可以在队列任意一端入队和出队。

　　

双端队列的常用操作

• Deque() 创建一个空的双端队列
• add_front(item) 从队头加入一个item元素
• add_rear(item) 从队尾加入一个item元素
• remove_front() 从队头删除一个item元素
• remove_rear() 从队尾删除一个item元素
• is_empty() 判断双端队列是否为空
• size() 返回队列的大小

五、双端队列的python代码实现

class Deque(object):
    """双端队列"""
    def __init__(self):
        self.items = []
        print("初始化双端队列")
 
    def is_empty(self):
        """判断队列是否为空"""
        return self.items == []
 
    def add_front(self, item):
        """在队头添加元素"""
        print("%d在队首进入队列"%item)
        self.items.insert(0,item)
 
    def add_rear(self, item):
        """在队尾添加元素"""
        print("%d在队尾进入队列"%item)
        self.items.append(item)
 
    def remove_front(self):
        """从队头删除元素"""
        item = self.items[0]
        print("%d从队首出队列"%item)
        return self.items.pop(0)
 
    def remove_rear(self):
        """从队尾删除元素"""
        print("%d从队尾出队列"%self.items[len(self.items)-1])
        return self.items.pop()
 
    def size(self):
        """返回队列大小"""
        return len(self.items)
 
    def travel(self):
        if len(self.items)==0:
            print("你要遍历的队列是空队列")
        else:
            print("你要遍历的队列元素有：",end=" ")
            for i in range(0,len(self.items)):
                print("%d "%self.items[i],end=" ")
            print("\n")
 
if __name__ == "__main__":
    deque = Deque()
    deque.add_front(1)
    deque.add_front(2)
    deque.add_rear(3)
    deque.add_rear(4)
    deque.travel()
    print("队列长度为：%d\n"%deque.size())
    deque.remove_front()
    deque.travel()
    deque.remove_front()
    deque.travel()
    deque.remove_rear()
    deque.travel()
    deque.remove_rear()
    deque.travel()

运行结果为：

初始化双端队列
1在队首进入队列
2在队首进入队列
3在队尾进入队列
4在队尾进入队列
你要遍历的队列元素有： 2  1  3  4  
 
队列长度为：4
 
2从队首出队列
你要遍历的队列元素有： 1  3  4  
 
1从队首出队列
你要遍历的队列元素有： 3  4  
 
4从队尾出队列
你要遍历的队列元素有： 3  
 
3从队尾出队列
你要遍历的队列是空队列

六、双端队列的C语言代码实现

//  main.m
//  双端队列
//  Created by 侯垒 on 2019/7/4.
//  Copyright © 2019 可爱的侯老师. All rights reserved.
#include<stdio.h>
 
// 创建队列的节点结构体
typedef struct N
{
    int num;
    struct N *next;
}Node;
 
// 创建节点
Node * createNode(int num)
{
 
    Node *node = (Node *)malloc(sizeof(Node));
    node->num = num;
    node->next = NULL;
    return node;
}
 
// 创建双端队列
Node * createDeQue()
{
    printf("初始化队列\n");
    Node *head = NULL;
    return head;
}
 
// 判断是否为空
int is_empty(Node *head)
{
    if (head == NULL)
    {
        return ;
    }
    else
    {
        return ;
    }
}
 
// 求双向队列的长度
int length(Node *head)
{
    Node *current = head;
    if (is_empty(head))
    {
        return ;
    }
    int count = ;
    while (current->next!=NULL)
    {
        count++;
        current = current->next;
    }
    return count;
}
 
// 头部插入
Node *add_front(Node *head, int num)
{
    Node *node = createNode(num);
    Node *current = head;
    if (is_empty(head)==)
    {
        head = node;
    }
    else
    {
        node->next = head;
        head = node;
    }
    printf("%d从队列头部进入队列\n",num);
    return head;
}
 
// 尾部插入
Node *add_rear(Node *head,int num)
{
    Node *node = createNode(num);
    if (is_empty(head)==)
    {
        head = add_front(head, num);
    }
    else
    {
        Node *current = head;
        while (current->next != NULL)
        {
            current = current->next;
        }
        current->next = node;
    }
    printf("%d从尾部进入队列\n",num);
    return head;
}
 
// 头部删除
Node *remove_front(Node *head)
{
    if (is_empty(head) == )
    {
        printf("这是一个空队列");
        return head;
    }
    else
    {
 
        int num = head->num;
        //head->next = head->next->next;
        printf("%d从队列头部出队列\n",num);
        head = head->next;
        return head;
    }
}
 
// 尾部删除
Node *remove_rear(Node *head)
{
    if (is_empty(head) == )
    {
        printf("这是一个空队列");
        return head;
    }
    else if (length(head) == )
    {
         head = remove_front(head);
         return head;
    }
    else
    {
        Node *current = head;
        for (int i=; i<length(head)-; i++)
        {
            current = current->next;
        }
        printf("%d从队列尾部出队列\n",current->next->num);
        current->next = NULL;
        return head;
    }
}
 
// 遍历
void travel(Node *head)
{
    if (is_empty(head) == )
    {
        printf("你遍历的队列为空\n");
    }
    else
    {
        printf("你要遍历的队列元素有：");
        Node *current = head;
        //printf("%d ",current->num);
        for (int i = ; i<length(head); i++)
        {
            printf("%d ",current->num);
            current = current->next;
        }
        printf("\n");
    }
}
 
int main(int argc, const char * argv[])
{
    Node *head = createDeQue();
    head = add_front(head, );
    travel(head);
    head = add_front(head, );
    travel(head);
    head = add_rear(head, );
    travel(head);
    head = add_rear(head, );
    travel(head);
 
    int  len = length(head);
    printf("现在队列的长度为%d\n",len);
 
    head = remove_front(head);
    travel(head);
    head = remove_front(head);
    travel(head);
    len = length(head);
    printf("现在队列的长度为%d\n",len);
    head = remove_rear(head);
    travel(head);
    head = remove_rear(head);
    travel(head);
 
    return ;
}

运行结果为：

初始化队列
1从队列头部进入队列
你要遍历的队列元素有：
2从队列头部进入队列
你要遍历的队列元素有：
3从尾部进入队列
你要遍历的队列元素有：
4从尾部进入队列
你要遍历的队列元素有：
现在队列的长度为4
2从队列头部出队列
你要遍历的队列元素有：
1从队列头部出队列
你要遍历的队列元素有：
现在队列的长度为2
4从队列尾部出队列
你要遍历的队列元素有：
3从队列头部出队列
你遍历的队列为空