Codeforces 1006F

题意略。

思路：

双向bfs。

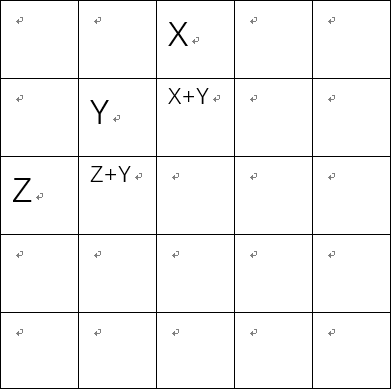
如图，对于曼哈顿距离为5的地方来说，除去两端的位置，其他位置的状态不会超过曼哈顿距离为4的地方的状态的两倍。

所以，最大曼哈顿距离为n + m。最多的状态不过2 ^ (n + m)。

这个复杂度我们不能接受，但是如果我们从两边向中间bfs的话， 每次bfs的复杂度为2 ^ ((n + m)/2)。

所以可以用双向广搜来解决。

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int maxn = ;
 
struct point{
    int x,y;
    LL state;
    point(int a = ,int b = ){
        x = a,y = b;
    }
    point operator+ (const point& p){
        return point(x + p.x,y + p.y);
    }
    int sum(){
        return x + y;
    }
    bool operator< (const point& p) const{
        if(x != p.x) return x < p.x;
        else if(y != p.y) return y < p.y;
        else return state < p.state;
    }
};
 
point mov1[] = {point(,),point(,)};
point mov2[] = {point(-,),point(,-)};
 
LL board[maxn][maxn];
LL n,m,k;
map<point,LL> mp;
 
void bfs1(point s){
    int line = ((n + m)>>) + ;
    s.state = board[s.x][s.y];
    queue<point> que;
    que.push(s);
    while(que.size()){
        point temp = que.front();
        que.pop();
        if(temp.sum() == line){
            ++mp[temp];
            continue;
        }
        for(int i = ;i < ;++i){
            point nxt = temp + mov1[i];
            if(nxt.x > n || nxt.y > m) continue;
            nxt.state = temp.state xor board[nxt.x][nxt.y];
            que.push(nxt);
        }
    }
}
LL bfs2(point s){
    LL ret = ;
    int line = ((n + m)>>) + ;
    s.state = k xor board[s.x][s.y];
    queue<point> que;
    que.push(s);
    while(que.size()){
        point temp = que.front();
        que.pop();
        if(temp.sum() == line){
            ret += mp[temp];
            continue;
        }
        for(int i = ;i < ;++i){
            point nxt = temp + mov2[i];
            if(nxt.x <  || nxt.y < ) continue;
            nxt.state = temp.state xor board[nxt.x][nxt.y];
            que.push(nxt);
        }
    }
    return ret;
}
 
int main(){
    scanf("%lld%lld%lld",&n,&m,&k);
    for(int i = ;i <= n;++i){
        for(int j = ;j <= m;++j){
            scanf("%lld",&board[i][j]);
        }
    }
    bfs1(point(,));
    int line = ((n + m)>>) + ;
    for(int i = ;i <= n;++i){
        int j = line - i;
        if(j <= ) continue;
        board[i][j] = ;
    }
    LL ans = bfs2(point(n,m));
    printf("%lld\n",ans);
    return ;
}