Codeforce Round #574(Div.2)

                                                                                                             A. Drinks Choosing

                                                                                                             time limit per test:2 seconds

                                                                                                       memory limit per test:256 megabytes

                                                                                                                     input:standard input

                                                                                                                     output:standard output

Old timers of Summer Informatics School can remember previous camps in which each student was given a drink of his choice on the vechorka (late-evening meal). Or may be the story was more complicated?

There are nn students living in a building, and for each of them the favorite drink aiai is known. So you know nn integers a1,a2,…,ana1,a2,…,an, where aiai (1≤ai≤k1≤ai≤k) is the type of the favorite drink of the ii-th student. The drink types are numbered from 11 to kk.

There are infinite number of drink sets. Each set consists of exactly two portions of the same drink. In other words, there are kk types of drink sets, the jj-th type contains two portions of the drink jj. The available number of sets of each of the kk types is infinite.

You know that students will receive the minimum possible number of sets to give all students exactly one drink. Obviously, the number of sets will be exactly ⌈n2⌉⌈n2⌉, where ⌈x⌉⌈x⌉ is xx rounded up.

After students receive the sets, they will distribute their portions by their choice: each student will get exactly one portion. Note, that if nn is odd then one portion will remain unused and the students' teacher will drink it.

What is the maximum number of students that can get their favorite drink if ⌈n2⌉⌈n2⌉ sets will be chosen optimally and students will distribute portions between themselves optimally?

Input

The first line of the input contains two integers nn and kk (1≤n,k≤10001≤n,k≤1000) — the number of students in the building and the number of different drinks.

The next nn lines contain student's favorite drinks. The ii-th line contains a single integer from 11 to kk — the type of the favorite drink of the ii-th student.

Output

Print exactly one integer — the maximum number of students that can get a favorite drink.

Examples

input

Copy

5 3
1
3
1
1
2

output

Copy

4

input

Copy

10 3
2
1
3
2
3
3
1
3
1
2

output

Copy

9

Note

In the first example, students could choose three sets with drinks 11, 11 and 22 (so they will have two sets with two drinks of the type 11 each and one set with two drinks of the type 22, so portions will be 1,1,1,1,2,21,1,1,1,2,2). This way all students except the second one will get their favorite drinks.

Another possible answer is sets with drinks 11, 22 and 33. In this case the portions will be 1,1,2,2,3,31,1,2,2,3,3. Then all the students except one will gain their favorite drinks. The only student that will not gain the favorite drink will be a student with ai=1ai=1 (i.e. the first, the third or the fourth).

题解：n个学生，k种类型的饮料，每个学生喜欢的饮料已列举出来，第一步判断学生人数的奇偶确定饮料组数，然后用数组存取读入的数字，每当存取2个同种类型的饮料饮料组数-1，ans+=2,a[i]清0

一个for循环,若此时饮料组数为0，结束循环，反之，饮料组数--，ans++，最后输出答案ans

 #include <bits/stdc++.h>
 using namespace std;
 const int N = 1e3 + ;
 int main()
 {
     ios::sync_with_stdio(false);
     cin.tie(); cout.tie();
     int n,k;
     int a[N];
     memset(a,,sizeof(a));
     cin>>n>>k;
     int re = (n / ) + (n & );
     int ans = ;
     for(int i = ; i <= n; i++)
     {
         int num;
         cin>>num;
         a[num]++;
         if(a[num] ==  && re)
         {
             ans += ;
             re--;
             a[num] = ;
         }
     }
     for(int i = ; i <= k; i++)
     {
         if(!re)
             break;
         if(a[i])
         {
             re--;
             ans++;
         }
     }
     cout<<ans<<endl;
     return ;
 }

B. Sport Mafia

                                                                                                   time limit per test：2 seconds

                                                                                             memory limit per test：256 megabytes

                                                                                                           input：standard input

                                                                                                         output：standard output

Each evening after the dinner the SIS's students gather together to play the game of Sport Mafia.

For the tournament, Alya puts candies into the box, which will serve as a prize for a winner. To do that, she performs nn actions. The first action performed is to put a single candy into the box. For each of the remaining moves she can choose from two options:

• the first option, in case the box contains at least one candy, is to take exactly one candy out and eat it. This way the number of candies in the box decreased by 11;
• the second option is to put candies in the box. In this case, Alya will put 11 more candy, than she put in the previous time.

Thus, if the box is empty, then it can only use the second option.

For example, one possible sequence of Alya's actions look as follows:

• put one candy into the box;
• put two candies into the box;
• eat one candy from the box;
• eat one candy from the box;
• put three candies into the box;
• eat one candy from the box;
• put four candies into the box;
• eat one candy from the box;
• put five candies into the box;

This way she will perform 99 actions, the number of candies at the end will be 1111, while Alya will eat 44 candies in total.

You know the total number of actions nn and the number of candies at the end kk. You need to find the total number of sweets Alya ate. That is the number of moves of the first option. It's guaranteed, that for the given nn and kk the answer always exists.

Please note, that during an action of the first option, Alya takes out and eats exactly one candy.

Input

The first line contains two integers nn and kk (1≤n≤1091≤n≤109; 0≤k≤1090≤k≤109) — the total number of moves and the number of candies in the box at the end.

It's guaranteed, that for the given nn and kk the answer exists.

Output

Print a single integer — the number of candies, which Alya ate. Please note, that in this problem there aren't multiple possible answers — the answer is unique for any input data.

Examples

input

Copy

1 1

output

Copy

0

input

Copy

9 11

output

Copy

4

input

Copy

5 0

output

Copy

3

input

Copy

3 2

output

Copy

1

Note

In the first example, Alya has made one move only. According to the statement, the first move is always putting one candy in the box. Hence Alya ate 00 candies.

In the second example the possible sequence of Alya's actions looks as follows:

• put 11 candy,
• put 22 candies,
• eat a candy,
• eat a candy,
• put 33 candies,
• eat a candy,
• put 44 candies,
• eat a candy,
• put 55 candies.

This way, she will make exactly n=9n=9 actions and in the end the box will contain 1+2−1−1+3−1+4−1+5=111+2−1−1+3−1+4−1+5=11 candies. The answer is 44, since she ate 44 candies in total.

题解：按照上述题干说的模拟，你有两个选择：第一：你可以吃掉一个，然后盒子里的糕点减一；第二：你可以放入糕点到盒子里去，但是每次放的比前一次的要多放一个。

 #include <bits/stdc++.h>
 using namespace std;
 int main()
 {
     ios::sync_with_stdio(false);
     cin.tie(); cout.tie();
     int n,k;
     cin>>n>>k;
     int ans = , sum = ,num = ;
     while(n--)
     {
         if(sum <= k)
         {
             num++;
             sum += num;
         }
         else if(sum > k)
         {
             sum--;
             ans++;
         }
     }
     cout<<ans<<endl;
     return ;
 }

                                                                                                               C. Basketball Exercise

                                                                                                              time limit per test：2 seconds

                                                                                                        memory limit per test：256 megabytes

                                                                                                                                  input：standard input

                                                                                                                                output：standard output

Finally, a basketball court has been opened in SIS, so Demid has decided to hold a basketball exercise session. 2⋅n2⋅n students have come to Demid's exercise session, and he lined up them into two rows of the same size (there are exactly nn people in each row). Students are numbered from 11 to nn in each row in order from left to right.

Now Demid wants to choose a team to play basketball. He will choose players from left to right, and the index of each chosen player (excluding the first one taken) will be strictly greater than the index of the previously chosen player. To avoid giving preference to one of the rows, Demid chooses students in such a way that no consecutive chosen students belong to the same row. The first student can be chosen among all 2n2n students (there are no additional constraints), and a team can consist of any number of students.

Demid thinks, that in order to compose a perfect team, he should choose students in such a way, that the total height of all chosen students is maximum possible. Help Demid to find the maximum possible total height of players in a team he can choose.

Input

The first line of the input contains a single integer nn (1≤n≤1051≤n≤105) — the number of students in each row.

The second line of the input contains nn integers h1,1,h1,2,…,h1,nh1,1,h1,2,…,h1,n (1≤h1,i≤1091≤h1,i≤109), where h1,ih1,i is the height of the ii-th student in the first row.

The third line of the input contains nn integers h2,1,h2,2,…,h2,nh2,1,h2,2,…,h2,n (1≤h2,i≤1091≤h2,i≤109), where h2,ih2,i is the height of the ii-th student in the second row.

Output

Print a single integer — the maximum possible total height of players in a team Demid can choose.

Examples

input

Copy

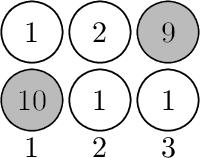
5
9 3 5 7 3
5 8 1 4 5

output

Copy

29

input

Copy

3
1 2 9
10 1 1

output

Copy

19

input

Copy

1
7
4

output

Copy

7

Note

In the first example Demid can choose the following team as follows:

In the second example Demid can choose the following team as follows:

题意：总共有2n个人，第一排和第二排都是编号从1到n，现在让你选择任意多个人使身高总和最大，条件限制同一个编号只能有一个人，编号相邻的人不可以在同一排。

题解：1.确定状态：dp[i][j]表示编号为i的人选择状态为j时的最大身高。

           2.确定状态转移方程：dp[i][j] = dp[i][j] + max(dp[i+1][j-2],dp[i+1][j-1])

           3.确定编程实现方式：for(ll i = 2; i <= n; i++)

                                              {

                                                   dp[1][i] += max(dp[2][i-2],dp[2][i-1]);

                                                   dp[2][i] += max(dp[1][i-2],dp[1][i-1]);

                                               }

                                               cout<<max(dp[1][n],dp[2][n])<<endl;

 #include <bits/stdc++.h>
 #define ll long long
 using namespace std;
 const int N = 1e5 + ;
 ll dp[][N];
 int main()
 {
     ios::sync_with_stdio(false);
     cin.tie(); cout.tie();
     int n;
     cin>>n;
     for(int i = ; i <= n; i++)
         cin>>dp[][i];
     for(int i = ; i <= n; i++)
         cin>>dp[][i];
     for(int i = ; i <= n; i++)
     {
         dp[][i] += max(dp[][i-],dp[][i-]);
         dp[][i] += max(dp[][i-],dp[][i-]);
     }
     cout<<max(dp[][n],dp[][n])<<endl;
     return ;
 }

优化后的AC代码：

 #include <bits/stdc++.h>
 #define ll long long
 using namespace std;
 const int N = 1e5 + ;
 ll dp[][N];
 ll val[][N];
 int main()
 {
     ios::sync_with_stdio(false);
     cin.tie(); cout.tie();
     int n;
     cin>>n;
     for(int i = ; i <= n; i++)
         cin>>val[][i];
     for(int i = ; i <= n; i++)
         cin>>val[][i];
     for(int i = ; i <= n; i++)
         for(int j = ; j <=; j++)
             dp[j][i] = max(dp[j][i-],dp[-j][i-]+val[j][i]);
     cout<<max(dp[][n],dp[][n])<<endl;
     return ;
 }