[考试反思]1028csp-s模拟测试91：预估

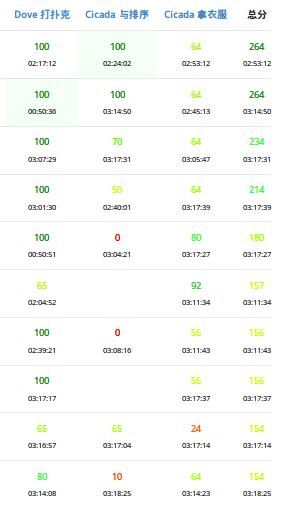
这一轮是要闹哪样啊？？？前十都死活进不去？？？

能不能不要到联赛前突然连续掉链子啊！！！

总算难得的切掉了T1。然后又一次把T2和T3的难度估反了

结果给T2剩下了30分钟，想到正解来不及打了。

然后T3没有乱搞丢了很多分。（循环不用跑满，上限能到80。。。考后还有AC的）

联赛题目的难度基本是升序。。。

学会乱搞，要有信仰。。。

T1必须占用更少的时间，想到并证明正确之后就快速打出来

T1：Dave打扑克

可以证明，数量本质不同的堆数至多为根号个。

所以并查集维护，用unordered_set迭代器遍历，用树状数组计数询问即可。

 #include<cstdio>
 #include<unordered_set>
 using namespace std;
 unordered_set<int>S;
 int n,m,t[],buc[],siz[],f[];
 void add(int p,int w){for(;p<=;p+=p&-p)t[p]+=w;}
 int ask(int p,int a=){for(;p;p^=p&-p)a+=t[p];return a;}
 int find(int p){return f[p]==p?p:f[p]=find(f[p]);}
 int main(){//freopen("cards105.in","r",stdin);freopen("my.out","w",stdout);
     scanf("%d%d",&n,&m);
     buc[]=n;S.insert();add(,n);
     for(int i=;i<=n;++i)f[i]=i,siz[i]=;
     for(int i=,opt,x,y;i<=m;++i){
         scanf("%d",&opt);
         if(opt==){
             scanf("%d%d",&x,&y);
             x=find(x);y=find(y);
             if(x==y)continue;
             add(siz[x],-);add(siz[y],-);add(siz[x]+siz[y],);
             buc[siz[x]]--;buc[siz[y]]--;buc[siz[x]+siz[y]]++;
             if(!buc[siz[x]])S.erase(siz[x]);
             if(!buc[siz[y]])S.erase(siz[y]);
             if(buc[siz[x]+siz[y]]==)S.insert(siz[x]+siz[y]);
             siz[y]+=siz[x];f[x]=y;n--;
         }else{
             scanf("%d",&x);long long ans=n*(n-1ll)>>;
             if(!x){printf("%lld\n",ans);continue;}
             unordered_set<int>::iterator it=S.begin();
             while(it!=S.end()){
                 y=*it;
                 ans-=1ll*buc[y]*(ask(y+x-)-ask(y));
                 ans-=1ll*buc[y]*(buc[y]-)>>;
                 it++;
             }printf("%lld\n",ans);
         }
     }
 }

T2：Cicada与排序

归并排序每个数也就会递归下去log层。

所以我们不断考虑每个数在参与一次归并后的相对排名就好了。

当然数字不一样的最后排名肯定好说，现在只考虑每个数在所有与它相同的数里的相对排名（以下简称“位置”）

设rk[i][j]表示最开始位置在i的数在归并后所在的位置。

然后我们考虑如何转移，我们需要的其实就是一个“两个数组归并，其中第一个数组的第p位在归并后的数组排第q位的概率”

这个可以dp求出。dp[i][j][0/1]表示归并排序时第一个数组弹掉了i个，第二个数组弹掉了j个，最后一次弹的来自于第一组还是第二组。

这样的话最后弹掉的元素就是排名第i+j的元素了，而在归并之前的排名就是i或j（取决于来源）

具体的转移其实就是考虑两个数组是不是已经被弹干净了，弹干净了一个那就只能弹另一个，否则就随机弹一个

转移比较简单，自己想比较好（这个已经比题解的那个简单很多了）实在不行再颓码

这个dp数组当然与两个原数组的长度有关，所以要放在merge_sort里面处理，而非全局预处理（这不是题解思路）

然后rk也就可以转移了，枚举归并前后的排名即可。

不要memset。跑的很快的。

复杂度的证明可能要等到学积分？极端数据是所有数都相同。

并不是积分，是主定理啦！

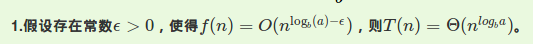
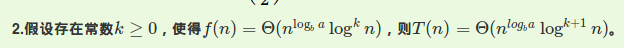
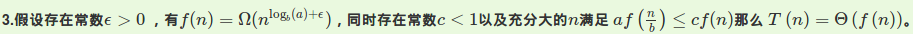
这道题满足第三条。$f(n)=\Omega (n^3)$，

这样的话$\epsilon =2>0$

此时c取$\frac{1}{4}$时满足后者条件即

$2f(\frac{n}{2})<=\frac{1}{4}f(n)$，其中$a=b=2$

所以总复杂度$O(n^3)$

 #include<bits/stdc++.h>
 using namespace std;
 #define mod 998244353
 #define inv 499122177
 #define int long long
 vector<int>lv[],rv[];
 int n,x[],rk[][],Rcnt[],Lcnt[],tem[],dp[][][];
 void merge_sort(int l,int r){
     if(l==r)return; int M=l+r>>;
     merge_sort(l,M); merge_sort(M+,r);
     for(int i=l;i<=M;++i)Lcnt[x[i]]++,lv[x[i]].push_back(i);
     for(int i=M+;i<=r;++i)Rcnt[x[i]]++,rv[x[i]].push_back(i);
     for(int i=;i<=;++i){
         for(int L=;L<=Lcnt[i];++L)for(int R=;R<=Rcnt[i];++R)dp[L][R][]=dp[L][R][]=;
         dp[][][]=;
         for(int L=;L<=Lcnt[i];++L)for(int R=;R<=Rcnt[i];++R)
             if(L!=Lcnt[i]&&R!=Rcnt[i])
                 dp[L+][R][]=(dp[L+][R][]+(dp[L][R][]+dp[L][R][])*inv)%mod,
                 dp[L][R+][]=(dp[L][R+][]+(dp[L][R][]+dp[L][R][])*inv)%mod;
             else if(L!=Lcnt[i])dp[L+][R][]=(dp[L+][R][]+dp[L][R][]+dp[L][R][])%mod;
             else if(R!=Rcnt[i])dp[L][R+][]=(dp[L][R+][]+dp[L][R][]+dp[L][R][])%mod;
         for(int j=;j<Lcnt[i];++j){
             for(int k=;k<=Lcnt[i];++k)for(int rp=;rp<=Rcnt[i];++rp)
                 tem[k+rp]=(tem[k+rp]+rk[lv[i][j]][k]*dp[k][rp][])%mod;
             for(int nrk=;nrk<=Lcnt[i]+Rcnt[i];++nrk)rk[lv[i][j]][nrk]=tem[nrk],tem[nrk]=;
         }
         for(int j=;j<Rcnt[i];++j){
             for(int k=;k<=Rcnt[i];++k)for(int lp=;lp<=Lcnt[i];++lp)
                 tem[k+lp]=(tem[k+lp]+rk[rv[i][j]][k]*dp[lp][k][])%mod;
             for(int nrk=;nrk<=Lcnt[i]+Rcnt[i];++nrk)rk[rv[i][j]][nrk]=tem[nrk],tem[nrk]=;
         }
         lv[i].clear();rv[i].clear();Lcnt[i]=Rcnt[i]=;
     }
 }
 main(){//freopen("sort103.in","r",stdin);
     scanf("%lld",&n);
     for(int i=;i<=n;++i)scanf("%lld",&x[i]);
     for(int i=;i<=n;++i)rk[i][]=;
     merge_sort(,n);
     for(int i=;i<=n;++i)Lcnt[x[i]]++;
     for(int i=;i<=;++i)Lcnt[i]+=Lcnt[i-];
     for(int i=;i<=n;++i){
         int ans=;
         for(int j=;j<=Lcnt[x[i]]-Lcnt[x[i]-];++j)ans=(ans+1ll*rk[i][j]*j)%mod;//,printf("%lld %lld\n",j,rk[i][j]);
         printf("%lld ",ans+Lcnt[x[i]-]);
     }puts("");
 }

T3：Cicada拿衣服

英文题目名为什么叫naive？？拿（na）衣（i）服（ve）？？？

看到这个题目名我还以为这道题真的很naive

其实只是比较好打，但是思路不是很好想

首先你需要打一个暴力，需要一个ST表来O(1)查询区间的那四个函数。

发现Dybala的ST表还是O(log)的。。。奉劝各位好好学学ST表。。。

highbit操作是要预处理的！！！不要现算！！！

然后最粗暴的就是枚举左右端点，check它的excited值，如果合法就区间取max。我是用线段树维护的。

到这里为止如果你不乱搞你能有36分。

然后正解的80%就已经打完了。

首先我们固定右端点，不断左移左端点。

对于OR，最多只会变化log次，即每一位从0变成1。

对于AND，最多也只会变化log次，每一位从1到0。

所以其实OR-AND只会变化2log次。

那么问题就是MIN-MAX了。MIN越来越小MAX越来越大所以MIN-MAX会越来越小。

所以在由OR-AND分割出的2log段里，每一段内部的excited值都满足单调性。

所以我们只要考虑在每一段里找到最靠左的excited值的合法位置，然后就线段树区间赋取max就好了。

然后怎么找到这2log个段呢？

用链表记录下每个段的右端点就好了，然后跳链表就可以。

因为右端点右移的时候，链表内部只会合并段而不会新增段，所以是可以用链表的。

所以代码其实只是多了一个链表，然后爆扫改成跳链表而已。

复杂度是$O(nlogn)$

这题数据很难造，所以乱搞可过。然而打正解需要优化常数不然容易T92什么的。。。

记得及时跳出不然还是$nlog^2$。。。我就是hanpi

 #include<bits/stdc++.h>
 using namespace std;
 int mx[][],mn[][],Or[][],And[][];
 int ans[],n,x[],hi[],k,t[],cl[],cr[];
 int lst[],nxt[];
 void del(int p){lst[nxt[p]]=lst[p];nxt[lst[p]]=nxt[p];}
 const int N=1e6+;
 const int Ls=<<|;
 char buffer[Ls],*Ss,*Ts;
 #define getchar() ((Ss==Ts&&(Ts=(Ss=buffer)+fread(buffer,1,Ls,stdin),Ss==Ts))?EOF:*Ss++)
 int read(register int p=,register char ch=getchar()){
     while(ch<''||ch>'')ch=getchar();
     while(ch>=''&&ch<='')p=(p<<)+(p<<)+ch-'',ch=getchar();
     return p;
 }
 #define Max(a,b) ((a)>(b)?(a):(b))
 #define Min(a,b) ((a)<(b)?(a):(b))
 int _max(int l,int r){
     int x=hi[r-l+];
     return Max(mx[x][l],mx[x][r-(<<x)+]);
 }
 int _min(int l,int r){
     int x=hi[r-l+];
     return Min(mn[x][l],mn[x][r-(<<x)+]);
 }
 int _or(int l,int r){
     int x=hi[r-l+];
     return Or[x][l]|Or[x][r-(<<x)+];
 }
 int _and(int l,int r){
     int x=hi[r-l+];
     return And[x][l]&And[x][r-(<<x)+];
 }
 int excited(int l,int r){
     return _or(l,r)-_max(l,r)+_min(l,r)-_and(l,r);
 }
 void build(int p,int l,int r){
     cl[p]=l;cr[p]=r;t[p]=-;
     if(l==r)return;
     build(p<<,l,l+r>>);
     build(p<<|,(l+r>>)+,r);
 }
 void modify(int p,int l,int r,int w){
     if(l<=cl[p]&&cr[p]<=r)return t[p]=Max(t[p],w),(void);
     if(l<=cr[p<<]) modify(p<<,l,r,w);
     if(r>cr[p<<]) modify(p<<|,l,r,w);
 }
 void dfs(int p,int w){
     w=Max(w,t[p]);
     if(cl[p]==cr[p])return printf("%d ",w),(void);
     dfs(p<<,w); dfs(p<<|,w);
 }
 int chk(int l,int r,int R){
     while(l<r-)if(excited(l+r>>,R)>=k)r=l+r>>;else l=(l+r>>)+;
     if(excited(l,R)>=k)return l;return r;
 }
 int main(){//freopen("naive105.in","r",stdin);freopen("my.out","w",stdout);
     scanf("%d%d",&n,&k);build(,,n);
     for(int i=;i<=n;++i)x[i]=read(),lst[i]=i-,nxt[i]=i+;
     nxt[]=;
     for(int i=;i<=n;++i) mx[][i]=mn[][i]=Or[][i]=And[][i]=x[i];
     for(int j=;j<;++j)for(int i=;i+(<<j)-<=n;++i)
         mx[j][i]=Max(mx[j-][i],mx[j-][i+(<<j-)]),
         mn[j][i]=Min(mn[j-][i],mn[j-][i+(<<j-)]),
         Or[j][i]=Or[j-][i]|Or[j-][i+(<<j-)],
         And[j][i]=And[j-][i]&And[j-][i+(<<j-)];
     for(int j=;j<;++j)for(int i=<<j;i<<<j+&&i<=n;++i)hi[i]=j;
     for(int r=;r<=n;++r){
         for(int i=lst[r];i;i=lst[i])if(_or(nxt[i],r)==_or(i,r)&&_and(nxt[i],r)==_and(i,r))del(i);
         for(int i=nxt[],p;i<=r;i=nxt[i])if(excited(i,r)>=k){p=chk(lst[i]+,i,r),modify(,p,r,r-p+);break;}
     }
     dfs(,-);puts("");
 }