P2934 [USACO09JAN]安全出行

图论瞎搞......

solution：

按例化简：给定一个无向图，保证单源最短路唯一，求每个点到1号点的最短路最后一条边被封锁的情况下的最短路

乍一看，应该是次短路，但是稍微用脚趾头想想都能发现不是次短路.....

然后就乱搞了一发。秉承着我们的口号

暴力碾标算，n方过百万

我试着搞了一发暴力：先求出最短路径树（很重要），然后对于每一个点的父亲（前一个节点）进行dij拓展，不走被封的边，然后遇到目标点就退出（思路来源：旅行者）

然后我发现，不仅仅会T，甚至这个思路就是错的！！！

1、为什么会T：旅行者那题相当于只找一个最短边权当做最短路，因此dij的拓展过程可以认为是O（1）的；

2、为什么会wa：来看样例：

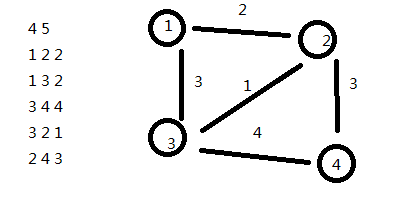
我弄出来的最短路径树是这样的：

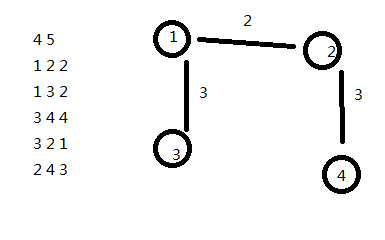
根据以上思路，只需要求出dis（最短路），还有从父亲节点拓展的dis，加起来即可。

但是，当走到2，拓展4的时候：拓展的非树边和之前的最短路加起来，变成了7！？

但是，如果换一条路走，答案应该是6......

所以，这个思路到此终结（我170+lines的代码啊！！！！）

正解：（对，没错，这里才开始正解）

首先，最短路径树的思路要保留，这里有一个比较玄学的式子：

min(dis(u,v)（边权）+dis（u）-dis（v）+dis（v)）；

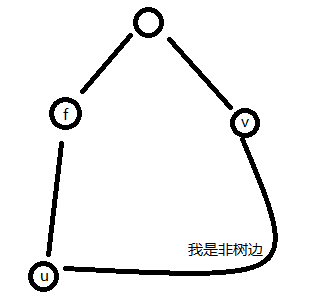
要求根到f的路径径，只需要知道根到u的最短路-根到f的最短路（也就是f到u的一条路径）加上根到v的最短路，再加上u到v的边权，这样就完成了一次拓展。

于是，就维护这个式子，用并查集维护联通（据机房大佬说这是并查集缩边233）

• 把所有非树边 记录下来
• 枚举点
• 更新式子
• 维护连通
• 进行n-1次

说明一下，为什么要用并查集：

因为排序，所以每一个点更新的第一次就是它的最优解，不需要更新第二次，所以用一个并查集来保证每个点只跑一次。

就是这样....据说spfa会被卡？本人专门卡各种卡spfa.....

就这样，我用玄学读优、流氓spfa，各种常数优化（好吧其实没有进行常数优化），跑进了某谷的最优解榜....

注意一下，要判断无解.....

（注释代码）

#include<bits/stdc++.h>
using namespace std;
const int maxn=1e6+;
int n,m;
inline int read()//当时为了跟旁边大佬比赛速度而加的读入优化
{
    int x=,f=;char s=getchar();
    while(s>''||s<''){if(s=='-')f=-;s=getchar();}
    while(s<=''&&s>=''){x=x*+s-'';s=getchar();}
    return f*x;
}
struct edge//前向星存边
{
    int to,next,dis;
}e[maxn];
int cnt,head[maxn];
inline void addedge(int from,int to,int dis)
{
    e[++cnt].next=head[from];
    e[cnt].to=to;
    e[cnt].dis=dis;
    head[from]=cnt;
}
int fa[maxn];
int dis[maxn];
struct cmp
{
    bool operator ()(int a,int b)
    {
        return dis[a]>dis[b];
    }
};//spfa优化
priority_queue <int,vector<int>,cmp> q;
int vis[maxn];
inline void spfa(int s)//比较普通得spfa
{
    for(int i=;i<=n;i++)
    {
        dis[i]=0x7fffffff;
        vis[i]=;
    }
    vis[s]=;
    dis[s]=;
    q.push(s);
    while(!q.empty())
    {
        int u=q.top();
        q.pop();
        vis[u]=;
        for(register int i=head[u];i;i=e[i].next)
        {
            int v=e[i].to;
            if(dis[v]>dis[u]+e[i].dis)
            {
                dis[v]=dis[u]+e[i].dis;
                fa[v]=u;//注意，最短路径树在此建立，在更新最短路的同时更新最短路径树上当前点的fa，也就是父节点，跑完spfa就能得到最短路径树了
                if(vis[v]==)
                {
                    vis[v]=;
                    q.push(v);
                }
            }
        }
    }
}

struct tree
{
    int u,v,w;
}a[maxn];//记录非树边
bool cmp(tree a,tree b)
{
    return a.w<b.w;//快排
}
int f[maxn],ans[maxn];
int num;
//int find(int x){return f[x]==x?x:f[x]=find(f[x]));}令附一行并查集
int find(int x)//不想一行并查集
{
    if(f[x]==x)
    return x;
    return f[x]=find(f[x]);
}
void solve(tree x)
{
    int u=x.u,v=x.v,t=x.w;
    while(find(u)!=find(v))//维护每个点只跑一次
    {
        num++;
        if(dis[find(u)]<dis[find(v)])
        swap(u,v);//确保两个点的顺序
        ans[find(u)]=min(ans[find(u)],t-dis[find(u)]);//更新
        u=f[find(u)]=fa[find(u)];//合并
    }
}
int tot;
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=;i<=m;i++)
    {
        int x,y,z;
        x=read();y=read();z=read();//scanf("%d%d%d",&x,&y,&z);
        addedge(x,y,z);
        addedge(y,x,z);
    }
    spfa();
    for(int i=;i<=cnt;i+=)
    {
        int u=e[i].to;//寻找非树边
        int v=e[i-].to;;
        if(u!=fa[v]&&v!=fa[u])//如果u和v不是最短路径树上的父子关系但是是一条边上的两个点
        {
            a[++tot].u=u;//它就是非树边
            a[tot].v=v;
            a[tot].w=e[i].dis+dis[u]+dis[v];//根据上述式子更新边权
        }
    }

    sort(a+,a++tot,cmp);//记得排序
    for(int i=;i<=n;i++)
    {
        f[i]=i;//并查集要初始化
        ans[i]=;
    }
    for(int i=;i<=tot&&num<n-;i++)
    {
        solve(a[i]);//对每个点进行更新
    }
    for(int i=;i<=n;i++)
    {
        if(ans[i]!=)
        printf("%d\n",ans[i]);
        else//判断无解
        printf("-1\n");
    }
    return ;
}

（完）