DFS深度优先算法学习

刚开始学习算法,参考大佬博客还是有很多不明白的,于是一步步解析,写下笔记记录。

大佬博客地址:

https://blog.csdn.net/fuzekun/article/details/85220468

问题描述
　　n个人参加某项特殊考试。
　　为了公平，要求任何两个认识的人不能分在同一个考场。
　　求是少需要分几个考场才能满足条件。
输入格式
　　第一行，一个整数n(1<n<100)，表示参加考试的人数。
　　第二行，一个整数m，表示接下来有m行数据
　　以下m行每行的格式为：两个整数a，b，用空格分开 (1<=a,b<=n) 表示第a个人与第b个人认识。
输出格式
　　一行一个整数，表示最少分几个考场。
样例输入
5
8
1 2
1 3
1 4
2 3
2 4
2 5
3 4
4 5
样例输出
4
样例输入
5
10
1 2
1 3
1 4
1 5
2 3
2 4
2 5
3 4
3 5
4 5
样例输出
5
因为数据量很小可以使用回溯算法。
应用两层回溯：
第一层回溯是将考生放在不同考场里面产生的效果，比如学生3号可以放在教室1和教室2中那么放在那一个教室会产生更好的效果这是一层回溯。
第二层回溯是考生放入以前的考场还是考生自己重新用一个考场。比如考生3号可以放进教室1和教室2，也可以放进教室3。
应用简单的剪枝技巧：
现在考场的数量已经大于以前最少的考场数量了就不用在展开了。
因为题目中没有时间限制，所以可以不使用vector,使用二维数组存放边，使用二维数组存放教室中学生。
另外使用vecot中的find()总是报错所以就不使用了
使用二维数组的时间复杂度约为O(nn)因为没一个学生需要遍历之前的考场就需要遍历每个人一次1 + 2…+n - 1;
使用vector最好的情况是NlogN,这种情况对应只有一个考场，每个学生耗费logN的复杂度,NlogN,最坏的情况就会退成O(NN)，对应着N个考场，每个之前的学生都需要遍历一次。

#include<stdio.h>
#include<iostream>
#include<vector>
#include<string.h>
using namespace std;
const int maxn = 100 + 5;
int room[maxn][maxn];//保存教室i中第j个学生的id
int gra[maxn][maxn];//存图
int m,n;
int res = maxn + 500;//保存答案
void solve(int id,int num)
{
    //printf("%d %d\n",id,num);
    if(num >= res){//剪枝
        return ;
    }
    if(id > n){//学生的编号从1开始防止room[][] = 0不是没学生的标志
        res = min(res,num);
        return ;
    }
    for(int i = 1;i <= num;i++){//找到id是否有符合的教室
        int k = 0,flag = 1;
        while(room[i][k]){//查找学生教室中是否有认识的人
           // printf("%d %d %d\n",id,room[i][k],gra[id][room[i][k]]);
            if(gra[id][room[i][k]]){//教室里面有认识的人
                //printf("冲突\n");
                flag = 0;
                break;
            }
            k++;//不要写在数组里面防止执行顺序的不对而出错
        }
        if(flag){                //回溯一定对应着判断
            room[i][k] = id;
            solve(id+1,num);
            room[i][k] = 0;        //第一层回溯
        }
    }
//重新开启一个教室
    room[num+1][0] = id;
    solve(id+1,num+1);
    room[num+1][0] = 0;//第二层回溯
}
void init()
{
    memset(room,0,sizeof(room));
}
int main()
{
    init();
    scanf("%d%d",&n,&m);
    for(int i = 0;i < m;i++){
        int a,b;
        scanf("%d%d",&a,&b);
        gra[a][b] = gra[b][a] = 1;
    }
    solve(1,0);
    printf("%d\n",res);
    return 0;
}

分析:
假设5个人，1，2，3，4，5    1，3，5互相认识
程序开始
输入 n=5 5个人  m=？命令数
初始 room[i][j] =0   i为房间，j为学生
输入
1 3
1 5
3 5
gra[1][3] = gra[3][1] =1
gra[1][5] = gra[5][1] =1
gra[3][5] = gra[5][3] =1
solve(id=1，num=0){  id为学生，num为房间数
    room[1][0] =1
    solve(id=2,num=1){
        room[1][1]=2
        solve(id=3,num=1){
            room[2][0]=3
            solve(id=4,num=2){
                room[1][2]=4
                solve(id=5，num=2){
                    room[3][0]=5
                    solve(id=6，num=3){
                        res=num=3
                        return
                    }
                    room[3][0]=0
                }
                room[1][2]=0
                room[2][1]=4
                solve(id=5,num=2){
                    room[3][0]=5
                    solve(id=6,num=3){
                        res=num=3
                        return
                    }
                    room[3][0]=0
                }
                room[2][1]=0
                room[3][0]=4
                solve(id=5,num=3){
                    3 >= 3 剪枝
                    return
                }
                room[3][0]=0
            }
            room[2][0]=0
        }
        room[1][1]=0
        room[2][0]=2
        solve(id=3,num=2){
            room[2][1]=3
            solve(id=4,num=2){
                room[1][1]=4
                solve(id=5,num=2){
                    room[3][0]=5
                    solve(id=6，num=3){
                        res =3
                        return
                    }
                    room[3][0]=0
                }
                room[1][1]=0
                room[2][2]=4
                solve(id=5，num=2){
                    room[3][0]=5
                    solve(id=6，num=3){
                        res =3
                        return
                    }
                    room[3][0]=0
                }
                room[3][0]=4
                solve(id=5,num=3){
                    剪枝
                    return
                }
            }
            room[2][1]=0
            room[3][0]=3
            solve(id=4,num=3){
                    剪枝
                    return
                }
        }
        room[2][0]=0
    }
    room[2][0]=2
    solve(id=3,num=2)
    ……
}

递归逻辑步骤
首先进入函数，
1判断当前的num屋子数是否大于等于已记录的屋子数res,如果符合则剪枝return
2判断当前的人id是否超过总人数,如果符合则记录当前屋子数res且return        
3循环判断现在的人id在已存在的num屋子数是否有认识人,如果没有则放在相应的后面
4创建一个新屋子,将现在的人放入,并将下一个人进行判断

假设过程:
id=1的人没有房子,开设新房子num=1并放入,
    递归id=2,发现num=1可以放入,
        递归id=3,发现num=1有认识的人,开设新房间num=2放入
            递归id=4,发现num=1可以放入
                递归id=5,发现num=1,num=2有认识的人,开设新房间num=3放入
                递归id=6,发现超过人数,记录下第一次得到的房间数res=num=3
            回溯id=4,不放进num=1,放入num=2
                递归id=5,发现num=1,num=2有认识的人,开设新房间num=3放入
                递归id=6,发现房间数num=3与res相等,表示不会出现更优解,进行剪枝
            回溯id=4,不放进num=1,num=2,开设新房间num=3
                递归id=5,发现房间数num=3与res相等,表示不会出现更优解,进行剪枝
            id=4停止
        id=3停止
    回溯id=2,开设新房间num=2放入
        递归id=3,发现num=1有认识的人,放入num=2中
            递归id=4,发现num=1可以放入
                递归id=5,发现num=1,num=2有认识的人,开设新房间num=3放入
                递归id=6,发现超过人数,记录下第一次得到的房间数res=num=3
            回溯id=4,不放进num=1,放入num=2
                递归id=5,发现num=1,num=2有认识的人,开设新房间num=3放入
                递归id=6,发现房间数num=3与res相等,表示不会出现更优解,进行剪枝
            回溯id=4,不放进num=1,num=2,开设新房间num=3
                递归id=5,发现房间数num=3与res相等,表示不会出现更优解,进行剪枝
            id=4停止
        递归id=3,开设新房间num=3,发现房间数num=3与res相等,表示不会出现更优解,进行剪枝
        id=3停止
    id=2停止
id=1停止

细节:首先进行剪枝判断来优化程序,当id数超过总人数表示一条支路到尽头,到尽头后往前回溯上一级的另外一种可能性,同样到尽头后再回溯,直到顶级结束
所有的回溯以开设新房间为最差方式结束。
思想核心:首先选择一个起点,先沿着一条路走到尽头,然后回溯上一步走另外一种可能,所有可能性走完后继续回溯上级再走上级的另外可能

总体的步骤图(差不多能看。。):

①

②

③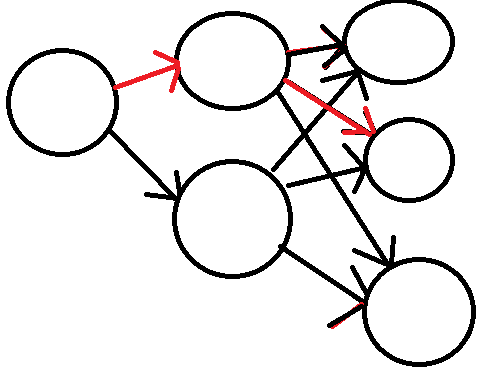

④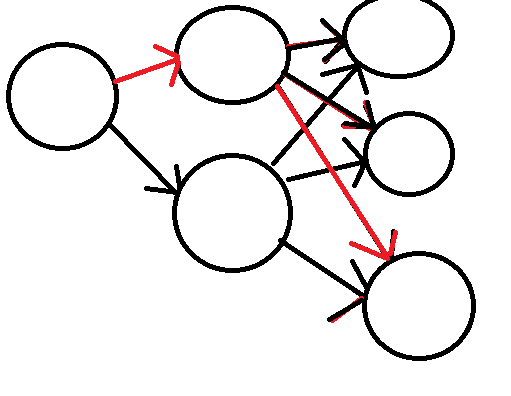

⑤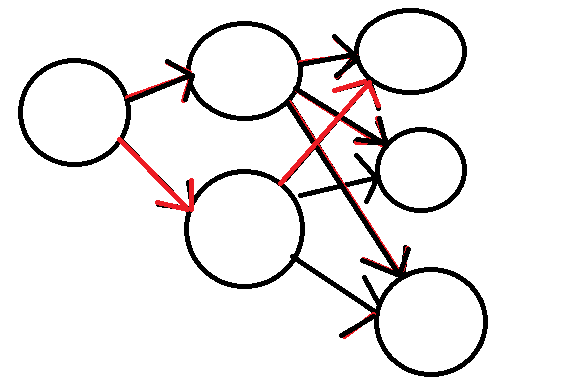

⑥

⑦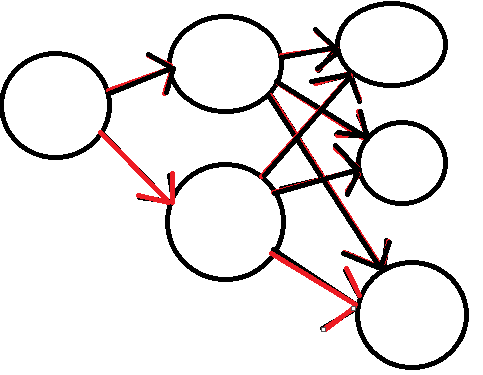

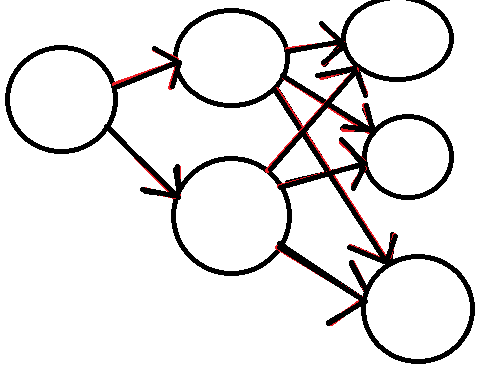(回到起点结束)