Dash Speed

Online Judge：NOIP2016十联测，Claris#2 T3

Label：好题，分治，并查集按秩合并，LCA

题目描述

比特山是比特镇的飙车圣地。在比特山上一共有 n 个广场，编号依次为 1 到 n，这些广场之间通过 n − 1 条双向车道直接或间接地连接在一起，形成了一棵树的结构。

因为每条车道的修建时间以及建筑材料都不尽相同，所以可以用两个数字 li, ri 量化地表示一条车道的承受区间，只有当汽车以不小于 li 且不大于 ri 的速度经过这条车道时，才不会对路面造成伤害。

Byteasar 最近新买了一辆跑车，他想在比特山飙一次车。Byteasar 计划选择两个不同的点 S, T ，然后在它们树上的最短路径上行驶，且不对上面任意一条车道造成伤害。

Byteasar 不喜欢改变速度，所以他会告诉你他的车速。为了挑选出最合适的车速，Byteasar 一共会向你询问 m 次。请帮助他找到一条合法的道路，使得路径上经过的车道数尽可能多。

输入

第一行包含两个正整数 n, m，表示广场的总数和询问的总数。

接下来 n − 1 行，每行四个正整数 ui, vi, li, ri，表示一条连接 ui 和 vi 的双向车道，且承受区间为[li, ri]。

接下来 m 行，每行一个正整数 qi，分别表示每个询问的车速。

输出

输出 m 行，每行一个整数，其中第 i 行输出车速为 qi 时的最长路径的长度，如果找不到合法的路径则输出 0。

样例

Input#1

Output#1

0
2
3

样例解释：

当车速为 1 时，不存在合法的路径。

当车速为 2 时，可以选择 1-5-4 这条路径，长度为 2。

当车速为 3 时，可以选择 3-2-1-5 这条路径，长度为 3

题解

Subtask1：暴力

对于每个询问直接枚举一个端点，然后dfs一遍，找最大距离。

时间复杂度为$O(M\cdot N^2)$，期望得分20。

Subtask2：树退化成链且l=1

由于l没有限制了，只要当前边的r大于等于限制lim，则可以通过。考虑离线询问，以r为关键字排序所有连边及询问，用并查集维护连通块，每个连通块记录两个值$ma，mi$，表示该连通块内节点的最大/最小深度，则当前连通块构成的链长度为$ma-mi$。

时间复杂度为$O(NlogN+M)$，结合Subtask1期望得分40。

Subtask3：树退化成链的所有情况

比起Subtask2，这里还要考虑l的限制。

枚举当前车速，则假如一条边限制车速为{$l,r$}，则在车速为$l$时加入这条连边，在车速为$r+1$时删除这条连边，对于每个车速，答案为当前所有连边形成的最大链长。

维护可以利用线段树。具体维护内容如下，对于线段树上的每个节点，设其对应树边范围为$(l,r)$，维护三个值$(li,ri,S)$，$li$表示$l$向右能延伸的最大连续长度，$ri$表示$r$向左能延伸的最大连续长度，$S$表示该区间内的最大链长。

时间复杂度为$O(NlogN+M)$，结合Subtask1期望得分60。

前面三种情况的切分代码如下：

#include<bits/stdc++.h>
using namespace std;
#define R register
bool nc1;
const int N=70010;
inline int read(){
    int x=0;char c=getchar();
    while(c<'0'||c>'9')c=getchar();
    while(c>='0'&&c<='9')x=(x<<3)+(x<<1)+(c^48),c=getchar();
    return x;
}
struct edge{
    int to,nxt,l,r;
}e[N<<1];
int ecnt,head[N];
inline void link(int u,int v,int l,int r){
    e[++ecnt]=(edge){v,head[u],l,r};
    head[u]=ecnt;
}
int n,m;
namespace SUB1_bl{//o(M*(N^2)):n,m<=20
    int now=0,lim;
    void dfs(int x,int f,int dis){
        if(dis>now)now=dis;
        for(int i=head[x];i;i=e[i].nxt){
            int y=e[i].to,l=e[i].l,r=e[i].r;
            if(y==f||lim<l||lim>r)continue;
            dfs(y,x,dis+1);
        }
    }
    void solve(){
        while(m--){
            lim=read();now=0;
            for(R int i=1;i<=n;++i)dfs(i,0,0);
            printf("%d\n",now);
        }
    }
}
struct EE{
    int x,d;
}E[N];
vector<int>que[N];
int res[N];
inline bool cmpsub2(EE a,EE b){return a.d<b.d;}
namespace SUB2_linkandL{//O(NlogN+M) 所有l=1且形态为链
    int ma[N],mi[N],CNT,tmp[N],bcj[N],ans=0;
    int find(int k){return bcj[k]==k?k:bcj[k]=find(bcj[k]);}
    void solve(){
        for(R int x=1;x<=n;x++){
            ma[x]=mi[x]=bcj[x]=x;
            for(R int i=head[x];i;i=e[i].nxt){
                int y=e[i].to;
                if(y==x+1){
                    E[++CNT]=(EE){x,e[i].r};
                    tmp[CNT]=e[i].r;
                    break;
                }
            }
        }
        sort(E+1,E+CNT+1,cmpsub2);
        sort(tmp+1,tmp+CNT+1);
        for(R int i=1;i<=m;++i){
            int qnum=read();
            qnum=lower_bound(tmp+1,tmp+CNT+1,qnum)-tmp;
            que[qnum].push_back(i);
        }
        for(R int i=CNT;i>=1;i--){
            int u=E[i].x,v=u+1,A=find(u),B=find(v);
            if(A==B)continue;
            bcj[A]=B;
            ma[B]=max(ma[B],ma[A]);
            mi[B]=min(mi[B],mi[A]);
            ans=max(ans,ma[B]-mi[B]);
            for(int j=0;j<que[i].size();++j)res[que[i][j]]=ans;
        }
        for(R int i=1;i<=m;++i)printf("%d\n",res[i]);
    }
}
typedef pair<int,int> pii;
vector<pii>g[N];
namespace SUB3_LINK{//链的所有情况
	struct SGT{
		int l,r;
		int S,li,ri;
		/*S:区间内最大连续链长
		  li:左端点向右的最大连续距离
		  ri:右端点向左的最大连续距离
		*/
	}b[N<<2];
	void build(int o,int l,int r){
		b[o].l=l,b[o].r=r,b[o].S=b[o].li=b[o].ri=0;
		if(l==r)return;
		int mid=l+r>>1;
		build(o<<1,l,mid),build(o<<1|1,mid+1,r);
	}
	void up(int o){
		int ls=o<<1,rs=o<<1|1;
		int sizL=b[ls].r-b[ls].l+1,sizR=b[rs].r-b[rs].l+1;
		b[o].S=max(max(b[ls].S,b[rs].S),b[ls].ri+b[rs].li);
		b[o].li=b[ls].li;
		if(b[ls].li==sizL)b[o].li+=b[rs].li;
		b[o].ri=b[rs].ri;
		if(b[rs].ri==sizR)b[o].ri+=b[ls].ri;
	}
	void update(int o,int pos,int z){
		if(b[o].l==b[o].r){
			b[o].S=b[o].li=b[o].ri=z;
			return;
		}
		int mid=b[o].l+b[o].r>>1;
		if(pos<=mid)update(o<<1,pos,z);
		else update(o<<1|1,pos,z);
		up(o);
	}
	void solve(){
		for(R int x=1;x<n;x++){
            for(R int i=head[x];i;i=e[i].nxt){
                int y=e[i].to;
                if(y==x+1){
                    g[e[i].l].push_back(make_pair(x,1));
                    g[e[i].r+1].push_back(make_pair(x,0));
                    break;
                }
            }
        }
        for(R int i=1;i<=m;i++){
			int x=read();
			que[x].push_back(i);
		}
		build(1,1,n-1);//n-1条线段
		for(R int i=1;i<=n;i++){
			for(R int j=0;j<g[i].size();j++)update(1,g[i][j].first,g[i][j].second);
			for(R int j=0;j<que[i].size();j++)res[que[i][j]]=b[1].S;
		}
        for(R int i=1;i<=m;i++)printf("%d\n",res[i]);
	}
}
bool nc2;
int main(){
    n=read(),m=read();
    bool islink=1,Lequal1=1;
    for(int i=1;i<n;++i){
        int u=read(),v=read(),l=read(),r=read();
        link(u,v,l,r);link(v,u,l,r);
        if(u!=v+1&&v!=u+1)islink=0;
        if(l!=1)Lequal1=0;
    }
	if(n<=20){SUB1_bl::solve();return 0;}
	if(islink&&Lequal1){SUB2_linkandL::solve();return 0;}
	if(islink){SUB3_LINK::solve();return 0;}
}

Subtask4：l=1的所有情况

只用考虑r的限制。

之前NOIP真题有做过类似的，好像是这题NOIP2013 货车运输。货车运输这题是给你每条路的承重量，多个询问，问你从u到v最多能带多少货物。做法是离线询问，从限制最宽(承重量最大)的边开始加，然后对于新生成的树启发式合并，维护两点连通情况，顺便更新答案。

两点连通情况不难维护，但本题需要维护的是新树的直径。

仍然基于Subtask2的想法，但是现在新树直径不是链长了。对于当前边$(x,y)$，如果已经同属于一棵树了就continue掉，反之对于分别属于的两棵树进行合并，并对新合并的树求直径。

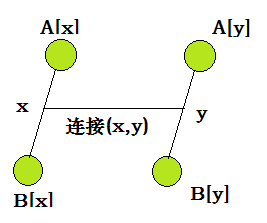
每个连通块(树)，维护两个东西{$A[],B[]$}，分别表示该连通块(树)的直径的两个端点。

对于合并后的新树，不难知道，新直径只可能有$C_4^2=6$种情况，即在原来的四个端点中选两个作为新树的端点，比较形成的直径长度，取6种中最长的一个更新。如何快速求两点距离呢？其实它就等于原树（所有边都连上时）上的距离，那么用树剖/倍增直接求LCA然后求原树上的距离即可。

时间复杂度为$O(NlogN+M)$，结合Subtask1,Subtask3期望得分80。

Subtask5：所有情况

现在还要考虑上l的限制了：（

由于车速处在$[1,n]$间，考虑预处理完所有$ans[i=1..n]$表示车速为i时能走的最长路径，然后直接在线回答询问。

考虑根据车速来分治。对于当前区间$[l,r]$，设道路限速为$[ql,qr]$。则将所有满足$ql<=l,r<=qr$的道路存在这个速度区间里（表示这个道路限度完全包含这个速度区间）。像下面这样：

//当前存的道路限速为[ql,qr]，当前车速区间为[l,r]，节点编号为o
//u,v是道路的两个端点
int head[N<<2],U[N*20],V[N*20],nxt[N*20],ecnt;
//大概N<<2个节点，大概会存N*logN次边
void Insert(int o,int l,int r,int ql,int qr,int u,int v){
	if(ql<=l&&r<=qr){
		U[++ecnt]=u;V[ecnt]=v;
		nxt[ecnt]=head[o];head[o]=ecnt;//前向星存边
		return;
	}
	int mid=l+r>>1;
	if(ql<=mid)Insert(o<<1,l,mid,ql,qr,u,v);
	if(qr>mid)Insert(o<<1|1,mid+1,r,ql,qr,u,v);
}

先来分析一下单单这样存边的复杂度，m条边每条边都存一次，递归层数为$logN$，所以$O(MlogN)$。顺便注意一下存边数组的大小。

存完边后开始分治连边。

//当前节点为o，速度区间为[l,r]，ret表示此时的树上最大链长
void solve(int o,int l,int r,int ret){
	int pos=cur;//cur和pos的具体用处下面会讲到
	for(R int i=head[o];i;i=nxt[i])merge(U[i],V[i],ret);
    //merge(u,v,ret)表示连接uv这条边，并更新当前ret
	if(l==r){
		ans[l]=ret;//当递归到叶子时得到ans
		Retrace(pos);//Retrace:回溯
		return;
	}
	int mid=l+r>>1;
	solve(o<<1,l,mid,ret);
	solve(o<<1|1,mid+1,r,ret);
	Retrace(pos);//分治到另一半时还得把当前这一半的影响给回溯了
}

merge函数的具体实现跟Substack4里讲的基本一样，利用并查集维护连通关系（但不能路径压缩，因为之后还要回溯）和当前树内的两个直径端点A[i],B[i],然后直接枚举$C_4^2=6$种情况，去更新新树的直径大小及端点。

代码如下：

int Find(int x){return fa[x]==x?x:Find(fa[x]);}
inline void Dia(int a,int b,int &P1,int &P2,int &ma){//考虑(a,b)作为新树直径的情况
	int tmp=dep[a]+dep[b]-2*dep[LCA(a,b)];//这个LCA在前面预处理出来，倍增或树剖
	if(tmp>ma)ma=tmp,P1=a,P2=b;//更新直径长度及两个端点
}
inline void merge(int x,int y,int &ret){//在(x,y)间连边，形成新树
	x=Find(x),y=Find(y);
	int P1,P2,ma=-1,tmp;
    //六种情况
	Dia(A[x],B[x],P1,P2,ma);
	Dia(A[x],A[y],P1,P2,ma);
	Dia(A[x],B[y],P1,P2,ma);
	Dia(B[x],A[y],P1,P2,ma);
	Dia(B[x],B[y],P1,P2,ma);
	Dia(A[y],B[y],P1,P2,ma);
	if(ma>ret)ret=ma;
	//!!!!
	if(rk[x]==rk[y]){//当两树秩相等时，将Treey连到Treex上，Treex的秩++
		rk[x]++;
		op[++cur]=(Op){0,x,0};
	}
	if(rk[x]<rk[y])swap(x,y);	
	op[++cur]=(Op){1,y,0};
	op[++cur]=(Op){2,x,A[x]};
	op[++cur]=(Op){3,x,B[x]};
	fa[y]=x,A[x]=P1,B[x]=P2;
    //!!!!
}

看到下面重点标记的部分，这一部分其实就是按秩合并两棵树，并且为之后的回溯操作做准备。

按秩合并的部分不难理解，就是将高度(秩)较小的树连在高度(秩)较大的树上。为回溯做准备的代码可以结合下面回溯代码去理解。

op这个结构体记录回溯操作，用类似栈的形式去存储回溯操作，cur就表示当前栈内元素(需要回溯的操作)。现在就可以解释之前分治函数solve()中这句代码的意义了int pos=cur;//cur和pos的具体用处下面会讲到，它存储了递归子树前栈顶的位置，现在我去分治另一半时只用回到pos位置即可。

struct Op{//记录回溯操作
	int t,x,y;
}op[N<<2];
inline void Retrace(int pos){//回溯到pos位置
	while(cur>pos){
		if(op[cur].t==0)rk[op[cur].x]--;
		if(op[cur].t==1)fa[op[cur].x]=op[cur].x;
		if(op[cur].t==2)A[op[cur].x]=op[cur].y;//还原该树直径端点1
		if(op[cur].t==3)B[op[cur].x]=op[cur].y;//还原该树直径端点2
		cur--;
	}
}

这样整个做法就结束了，具体实现时注意细节，包括数组大小/数组名混淆/不能路径压缩这些。

上面的分治做法看似非常暴力，来分析一下复杂度，边存储了$MlogN$次，每条边都至多merge()一次，每次合并产生的需要回溯操作不多，而每次操作都至多出栈一次，整个算法的时间复杂度大致为$O(Nlog^2N)$。

完整代码如下：

#include<bits/stdc++.h>
#define R register
using namespace std;
const int N=70010;
int n,m,cur,ans[N];
int sz[N],f[N],dep[N],son[N],top[N];//树剖
int fa[N],rk[N],A[N],B[N];//并查集 
int head[N<<2],U[N*20],V[N*20],nxt[N*20],ecnt;
inline int read(){
    int x=0;char c=getchar();
    while(c<'0'||c>'9')c=getchar();
    while(c>='0'&&c<='9')x=(x<<3)+(x<<1)+(c^48),c=getchar();
    return x;
}
struct Op{//记录回溯操作
	int t,x,y;
}op[N<<2];
vector<int>g[N];
void dfs(int x){
	sz[x]=1;
	for(int i=0;i<g[x].size();++i){
		int y=g[x][i];if(y==f[x])continue;
		f[y]=x,dep[y]=dep[x]+1;
		dfs(y),sz[x]+=sz[y];
		if(sz[y]>sz[son[x]])son[x]=y;
	}
}
void redfs(int x,int tp){
	top[x]=tp;
	if(son[x])redfs(son[x],tp);
	for(int i=0;i<g[x].size();++i){
		int y=g[x][i];if(y==f[x]||y==son[x])continue;
		redfs(y,y);
	}
}
inline int LCA(int x,int y){
	while(top[x]!=top[y]){
		if(dep[top[x]]<dep[top[y]])swap(x,y);
		x=f[top[x]];
	}
	return dep[x]<dep[y]?x:y;
}
int Find(int x){return fa[x]==x?x:Find(fa[x]);}
inline void Dia(int a,int b,int &P1,int &P2,int &ma){//考虑(a-b)作为新树直径的情况
	int tmp=dep[a]+dep[b]-2*dep[LCA(a,b)];
	if(tmp>ma)ma=tmp,P1=a,P2=b;
}
inline void merge(int x,int y,int &ret){//在(x,y)间连边，形成新树
	x=Find(x),y=Find(y);
	int P1,P2,ma=-1,tmp;
	Dia(A[x],B[x],P1,P2,ma);
	Dia(A[x],A[y],P1,P2,ma);
	Dia(A[x],B[y],P1,P2,ma);
	Dia(B[x],A[y],P1,P2,ma);
	Dia(B[x],B[y],P1,P2,ma);
	Dia(A[y],B[y],P1,P2,ma);
	if(ma>ret)ret=ma;
	if(rk[x]==rk[y]){//当两树秩相等时，将Treey连到Treex上，Treex的秩++
		rk[x]++;
		op[++cur]=(Op){0,x,0};
	}
	if(rk[x]<rk[y])swap(x,y);
	op[++cur]=(Op){1,y,0};
	op[++cur]=(Op){2,x,A[x]};
	op[++cur]=(Op){3,x,B[x]};
	fa[y]=x,A[x]=P1,B[x]=P2;
}
inline void Retrace(int pos){//回溯
	while(cur>pos){
		if(op[cur].t==0)rk[op[cur].x]--;
		if(op[cur].t==1)fa[op[cur].x]=op[cur].x;
		if(op[cur].t==2)A[op[cur].x]=op[cur].y;//还原该树直径端点1
		if(op[cur].t==3)B[op[cur].x]=op[cur].y;//还原该树直径端点2
		cur--;
	}
}
void Insert(int o,int l,int r,int ql,int qr,int u,int v){
	if(ql<=l&&r<=qr){
		U[++ecnt]=u;V[ecnt]=v;
		nxt[ecnt]=head[o];head[o]=ecnt;//存边
		return;
	}
	int mid=l+r>>1;
	if(ql<=mid)Insert(o<<1,l,mid,ql,qr,u,v);
	if(qr>mid)Insert(o<<1|1,mid+1,r,ql,qr,u,v);
}
void solve(int o,int l,int r,int ret){
	int pos=cur;
	for(R int i=head[o];i;i=nxt[i])merge(U[i],V[i],ret);
	if(l==r){
		ans[l]=ret;
		Retrace(pos);
		return;
	}
	int mid=l+r>>1;
	solve(o<<1,l,mid,ret);
	solve(o<<1|1,mid+1,r,ret);
	Retrace(pos);
}
int main(){
	n=read(),m=read();
	for(R int i=1;i<n;++i){
		int u=read(),v=read(),l=read(),r=read();
		g[u].push_back(v);
		g[v].push_back(u);
		Insert(1,1,n,l,r,u,v);
	}
	dfs(1);redfs(1,1);
	for(R int i=1;i<=n;++i)fa[i]=A[i]=B[i]=i;
	solve(1,1,n,0);
	while(m--)printf("%d\n",ans[read()]);
}

Dash Speed【好题，分治，并查集按秩合并】的更多相关文章

BZOJ4668: 冷战 [并查集按秩合并]
BZOJ4668: 冷战题意: 给定 n 个点的图.动态的往图中加边,并且询问某两个点最早什么时候联通,强制在线. 还可以这样乱搞并查集按秩合并的好处: 深度不会超过$O(\log n)$ ...
【bzoj4668】冷战并查集按秩合并+朴素LCA
题目描述 1946 年 3 月 5 日,英国前首相温斯顿·丘吉尔在美国富尔顿发表“铁幕演说”,正式拉开了冷战序幕. 美国和苏联同为世界上的“超级大国”,为了争夺世界霸权,两国及其盟国展开了数十年的斗争 ...
[CSP-S模拟测试]:Dash Speed（线段树+并查集+LCA）
题目描述比特山是比特镇的飙车圣地.在比特山上一共有$n$个广场,编号依次为$1$到$n$,这些广场之间通过$n−1$条双向车道直接或间接地连接在一起,形成了一棵树的结构. 因为每条车道的修建时间以及 ...
BZOJ4025 二分图分治并查集二分图带权并查集按秩合并
原文链接http://www.cnblogs.com/zhouzhendong/p/8683831.html 题目传送门 - BZOJ4025 题意有$n$个点,有$m$条边.有$T$个时间段.其中 ...
石头剪刀布（2019Wannafly winter camp day3 i）带权并查集+按秩合并好题
题目传送门思路: 按照题意描述,所有y挑战x的关系最后会形成一棵树的结构,n个人的总方案数是 3n 种,假设一个人被挑战(主场作战)a次,挑战别人(客场)b次,那么这个人存活到最后的方案数就是3n* ...
Codeforces Gym 101194G Pandaria （2016 ACM-ICPC EC-Final G题，并查集 + 线段树合并）
题目链接 2016 ACM-ICPC EC-Final Problem G 题意给定一个无向图.每个点有一种颜色. 现在给定$q$个询问,每次询问$x$和$w$,求所有能通过边权值不超过$w$的 ...
【BZOJ-4668】冷战并查集 + 按秩合并 + 乱搞
4668: 冷战 Time Limit: 10 Sec Memory Limit: 256 MBSubmit: 37 Solved: 24[Submit][Status][Discuss] Des ...
HDU——1213How Many Tables（并查集按秩合并）
J - How Many Tables Time Limit:1000MS Memory Limit:32768KB 64bit IO Format:%I64d & %I64u ...
NOIP2013 D1T3 货车运输倍增LCA OR 并查集按秩合并
思路: Kruskal求最大生成树+倍增LCA // by SiriusRen #include <cstdio> #include <cstring> #include &l ...

随机推荐

剑指offer——25链表中环的入口节点
题目描述给一个链表,若其中包含环,请找出该链表的环的入口结点,否则,输出null. 题解: 使用快慢指针即可,若快慢指针会相遇,则有环,否则快指针先到空节点: 此时,快指针从此处一次移一步遍历, ...
编译Solr4.72 源码没有成功
最近需要用到solr,查询Hbase里面的数据,编译Solr的时候遇到了点问题: 下了solr的源码后需要用ant自己编译: 源码下载地址:https://svn.apache.org/repos/a ...
【2018ACM/ICPC网络赛】徐州赛区
呃.自闭了自闭了.我才不会说我写D写到昏天黑地呢. I Characters with Hash 题目链接:https://nanti.jisuanke.com/t/31461 题意:给你一个字符串 ...
centos yum install 找不到软件包
yum install epel-release 然后再试试yum install 其他安装包
verifier 调试内存泄露
没啥技术含量,都是老段子了, 这次记下来,只是我想说,我也做过,留个念相. 前置条件,电脑里面必须得有Verifier,有了之后把自己的驱动加进去, WinDBG上双机,然后就可以跑了,跑一段时间就可 ...
2019 Multi-University Training Contest 3 B 支配树
题目传送门题意:给出衣服有向无环图(DAG),,定义出度为0的点为中心城市,每次询问给出两个点,求破坏任意一个城市,使得这两个点至少有一个点无法到达中心城市,求方案数. 思路:首先建立反向图,将城市 ...
Docker的镜像导出导入
查看当前已经安装的镜像 vagrant@vagrant:~$ sudo docker images REPOSITORY TAG IMAGE ID CREATED SIZE mysql 5.7.22 ...
es5 JSON对象
1. JSON.stringify(obj/arr) js对象(数组)转换为json对象(数组) 2. JSON.parse(json) json对象(数组)转换为js对象(数组) <!DOCT ...
Estimation
Estimation 给出一个长度为n序列$\{a_i\}$,将其划分成连续的K段,对于其中一段$[l,r]$,设其中位数为m,定义其权值为$\sum_{i=l}^r|m-a_i|$,求最 ...
Redhat镜像-RHEL-官方镜像下载大全
原网站内容链接:https://pan.baidu.com/s/12XYXh#list/path=%2F 已经存在自己的云盘上了

Dash Speed【好题，分治，并查集按秩合并】