第四十六篇 入门机器学习——kNN - k近邻算法(k-Nearest Neighbors)
No.1. k-近邻算法的特点

No.2. 准备工作,导入类库,准备测试数据

No.3. 构建训练集

No.4. 简单查看一下训练数据集大概是什么样子,借助散点图
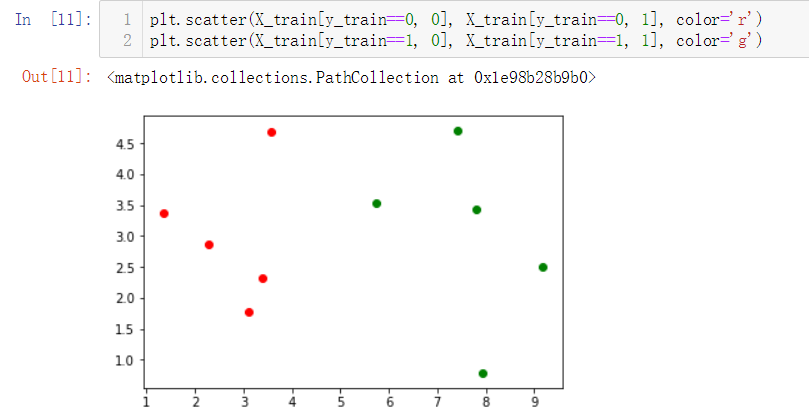

No.6. kNN的实现过程——计算x到训练数据集中每个点的距离
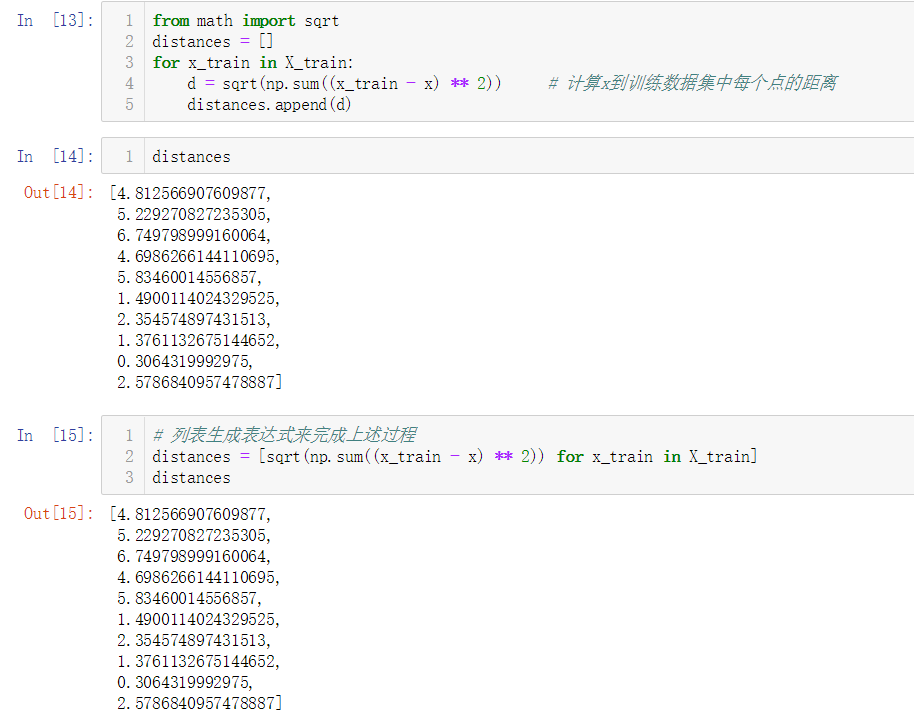
No.7. kNN的实现过程——使用argsort来获取距离x由近到远的点的索引组成的向量,进行保存

No.8. kNN的实现过程——指定需要考虑的最近的点的个数k,并获取距离x最近的k个点的y_train中的数据

No.9. kNN的实现过程——统计出属于不同类别的点的个数,并选择票数最多的类别
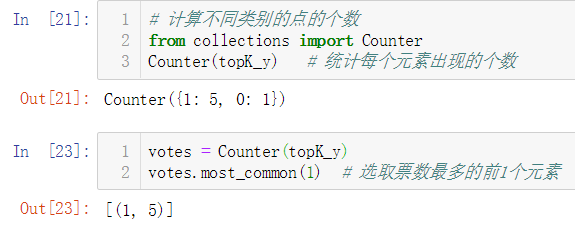
No.10. kNN的实现过程——对预测结果进行保存,结束。

No.11. 我们可以将kNN算法封装到一个函数中

No.12. 然后我们处理好测试数据,直接调用这个封装好的函数,就能得到预测结果
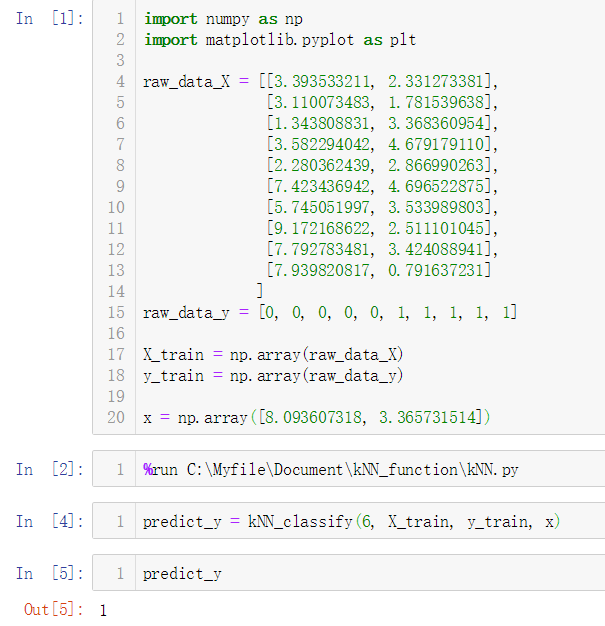
No.13. 机器学习的一般流程

No.14. k-近邻算法的特殊性

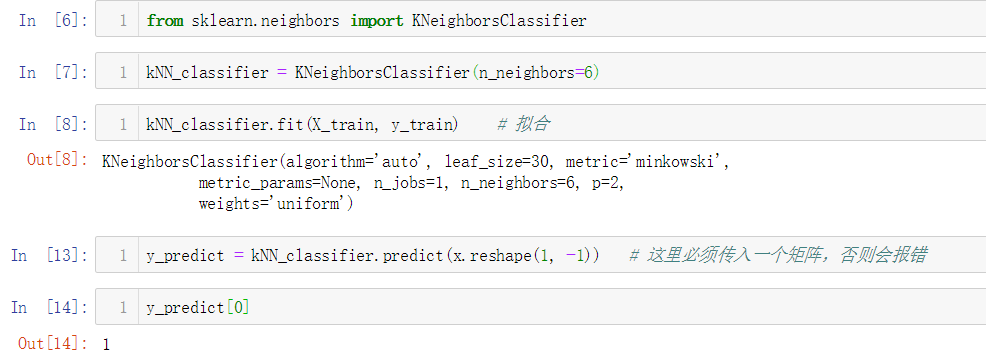
No.15. 使用scikit-learn中的kNN算法
No.16. 模仿scikit-learn封装自己的KNNClassifier类

No.17. 调用自己封装的KNNClassifier类

- 缺点1:效率低下,这也是kNN算法的最大缺点,如果训练数据集有m个样本,n个特征,则预测一个新数据的时间复杂度为O(m*n)
- 缺点2:高度数据相关,容易导致预测出错
- 缺点3:预测结果不具有可解释性
- 缺点4:维数灾难,随着维数的增加,原本看似很近的两个点的距离会越来越大

第四十六篇 入门机器学习——kNN - k近邻算法(k-Nearest Neighbors)的更多相关文章
- 第四十九篇 入门机器学习——数据归一化(Feature Scaling)
No.1. 数据归一化的目的 数据归一化的目的,就是将数据的所有特征都映射到同一尺度上,这样可以避免由于量纲的不同使数据的某些特征形成主导作用. No.2. 数据归一化的方法 数据归一化的方法主要 ...
- 第四十二篇 入门机器学习——Numpy的基本操作——索引相关
No.1. 使用np.argmin和np.argmax来获取向量元素中最小值和最大值的索引 No.2. 使用np.random.shuffle将向量中的元素顺序打乱,操作后,原向量发生改变:使用np. ...
- 第三十六篇 入门机器学习——Jupyter Notebook中的魔法命令
No.1.魔法命令的基本形式是:%命令 No.2.运行脚本文件的命令:%run %run 脚本文件的地址 %run C:\Users\Jie\Desktop\hello.py # 脚本一旦 ...
- Python之路(第四十六篇)多种方法实现python线程池(threadpool模块\multiprocessing.dummy模块\concurrent.futures模块)
一.线程池 很久(python2.6)之前python没有官方的线程池模块,只有第三方的threadpool模块, 之后再python2.6加入了multiprocessing.dummy 作为可以使 ...
- Jmeter(四十六) - 从入门到精通高级篇 - Jmeter之网页图片爬虫-下篇(详解教程)
1.简介 上一篇介绍了爬取文章,这一篇宏哥就简单的介绍一下,如何爬取图片然后保存到本地电脑中.网上很多漂亮的壁纸或者是美女.妹子,想自己收藏一些,挨个保存太费时间,那你可以利用爬虫然后批量下载. 2. ...
- 第四十六篇、UICollectionView广告轮播控件
这是利用人的视觉错觉来实现无限轮播,UICollectionView 有很好的重用机制,这只是部分核心代码,后期还要继续完善和代码重构. #import <UIKit/UIKit.h> # ...
- 第四十六篇--解析和保存xml文件
新建assets资源文件夹,右键app --> new --> Folder --> Assets Folder,将info.xml放入此文件夹下面. info.xml <?x ...
- 第三十九篇 入门机器学习——Numpy.array的基础操作——合并与分割向量和矩阵
No.1. 初始化状态 No.2. 合并多个向量为一个向量 No.3. 合并多个矩阵为一个矩阵 No.4. 借助vstack和hstack实现矩阵与向量的快速合并.或多个矩阵快速合并 No.5. 分割 ...
- 第三十八篇 入门机器学习——Numpy.array的基本操作——查看向量或矩阵
No.1. 初始化状态 No.2. 通过ndim来查看数组维数,向量是一维数组,矩阵是二维数组 No.3. 通过shape来查看向量中元素的个数或矩阵中的行列数 No.4. 通过size来查看数组中的 ...
随机推荐
- JS DOM属性+JS事件
DOM属性 console.log(ele.attributes) 获取ele元素的属性集合 ele.attributes.getNamesItem(attr).nodeValue 获取指定属性值 e ...
- Spark学习之路 (十九)SparkSQL的自定义函数UDF[转]
在Spark中,也支持Hive中的自定义函数.自定义函数大致可以分为三种: UDF(User-Defined-Function),即最基本的自定义函数,类似to_char,to_date等 UDAF( ...
- Flink架构,源码及debug
序 工作中用Flink做批量和流式处理有段时间了,感觉只看Flink文档是对Flink ProgramRuntime的细节描述不是很多, 程序员还是看代码最简单和有效.所以想写点东西,记录一下,如果能 ...
- 没有胆量,有天赋也是白费。Without guts,talent is wasted.
没有胆量,有天赋也是白费. Without guts,talent is wasted.
- 谈一谈php反序列化
1.序列化与反序列化 php中有两个函数serialize()和unserialize() 序列化serialize(): 当在php中创建了一个对象后,可以通过serialize()把这个对象转变成 ...
- 常见sql注入的类型
这里只讲解sql注入漏洞的基本类型,代码分析将放在另外一篇帖子讲解 目录 最基础的注入-union注入攻击 Boolean注入攻击-布尔盲注 报错注入攻击 时间注入攻击-时间盲注 堆叠查询注入攻击 二 ...
- LRU算法实现 最近最久未使用
1.LRU算法实现 最近最久未使用(蚂蚁金服笔试题,本人亲自经历的[苦笑.jpg]) 实现原理:数组 主要功能:初始化.入队列 主要操作:数组元素移动 代码: package com.ch.evalu ...
- VsCode开发Java SpringBoot遇到的问题
报错截图 报错一:Build failed, Do you want to continue? 编译失败,你想继续吗? 报错二:ConfigError:The Project "Demo&q ...
- yarn 不要一起用 npm
yarn 不要一起用 npm 如果一起用,看下lock 的版本一样不,不一样可能会出现问题
- Real-time Compressive Tracking
这是RTC算法的文献blog Real-time Compressive Tracking Kaihua Zhang1, Lei Zhang1, Ming-Hsuan Yang2 1Dept. of ...
