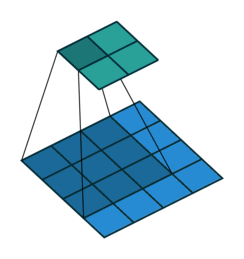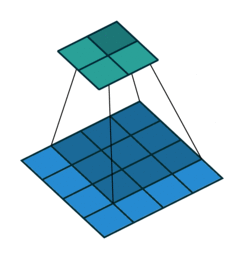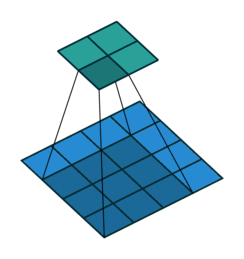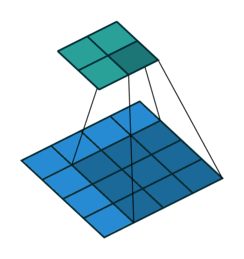
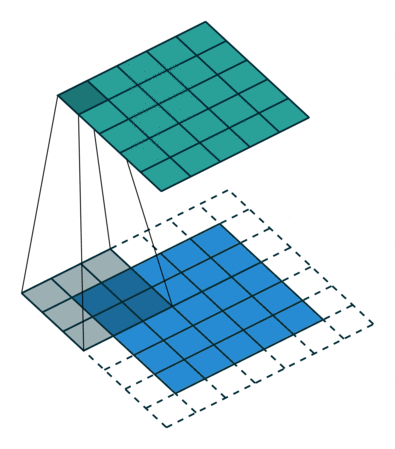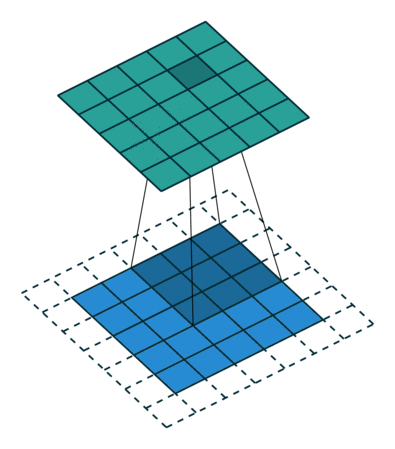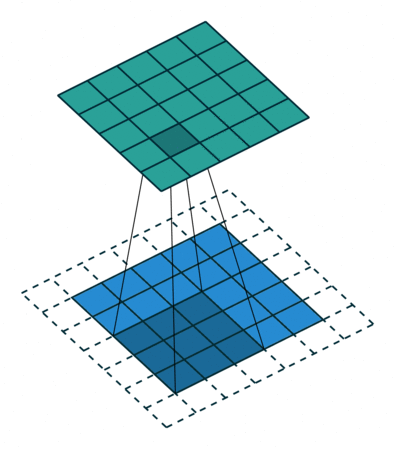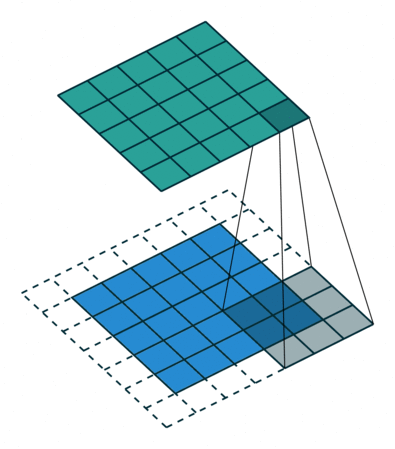
形象解释各种卷积算法(Convolution animations)
 |
 |
 |
 |
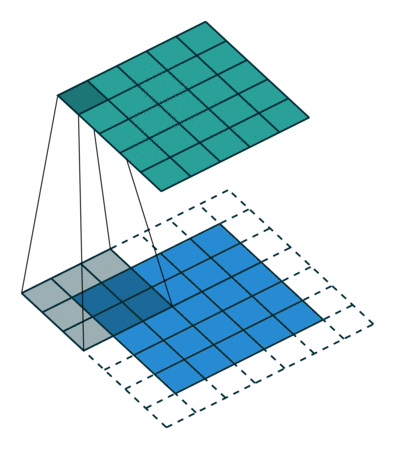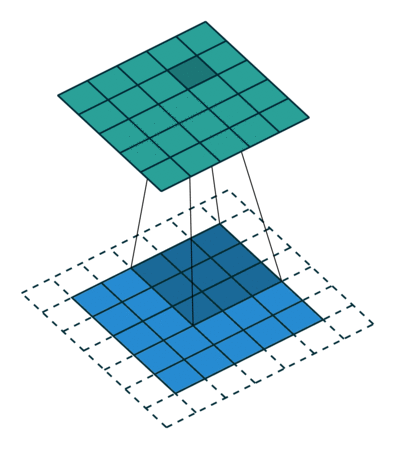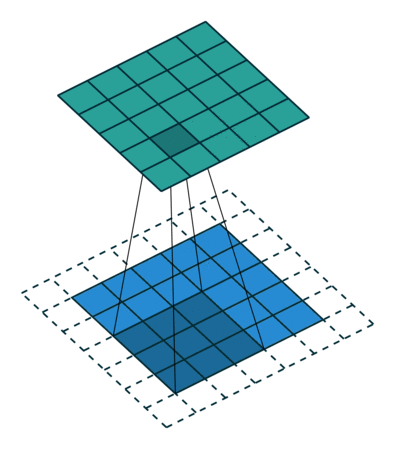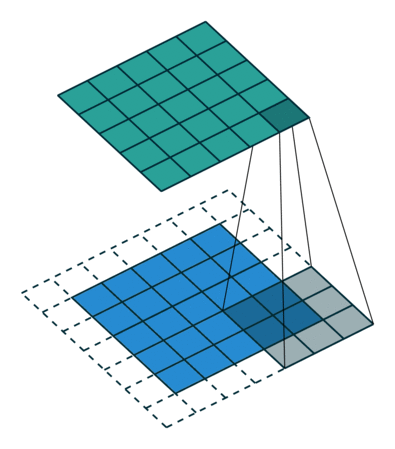
| No padding, no strides | Arbitrary padding, no strides | Half padding, no strides | Full padding, no strides |
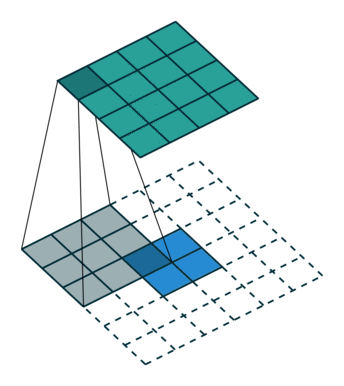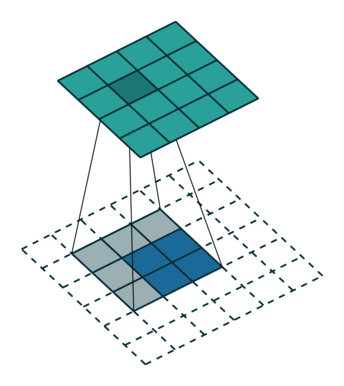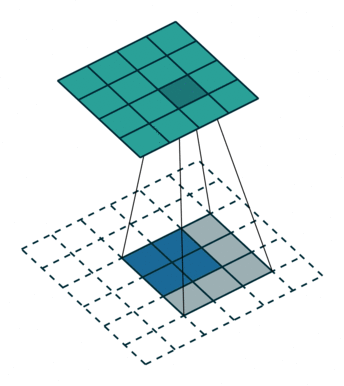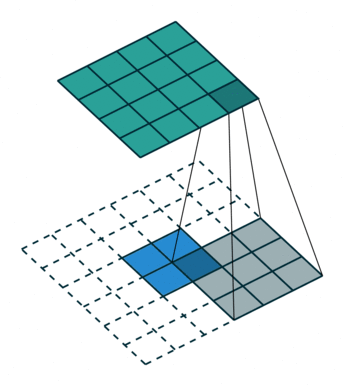 |
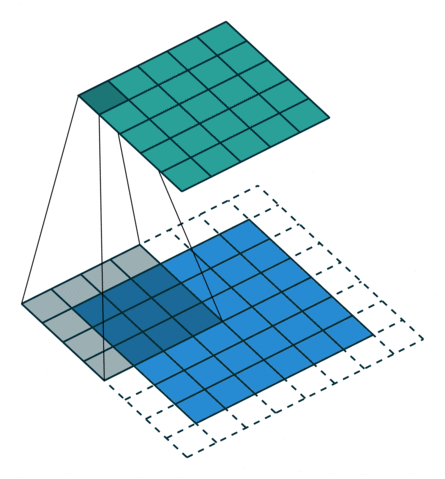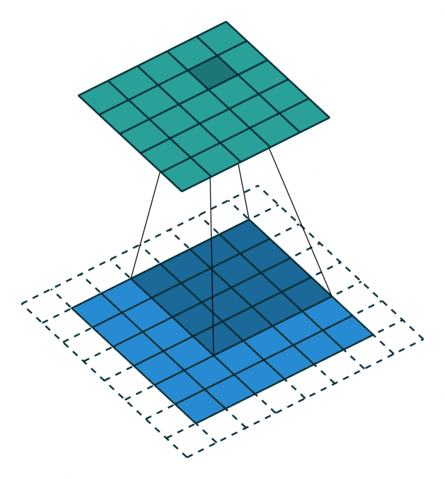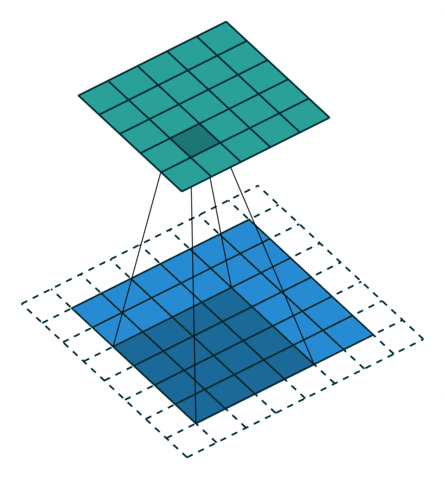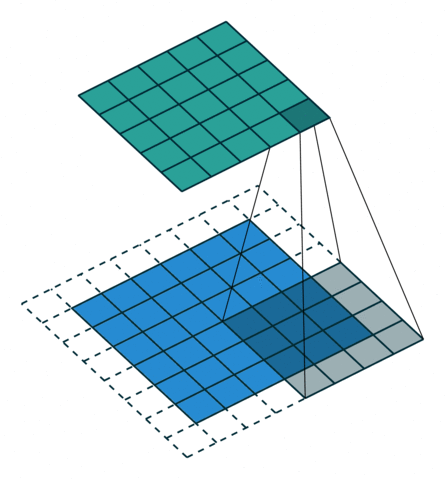 |
 |
 |
| No padding, no strides, transposed | Arbitrary padding, no strides, transposed | Half padding, no strides, transposed | Full padding, no strides, transposed |
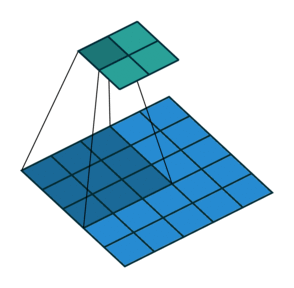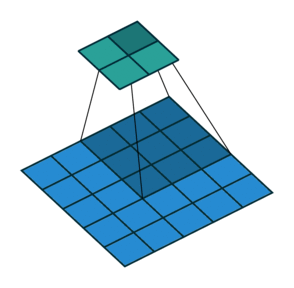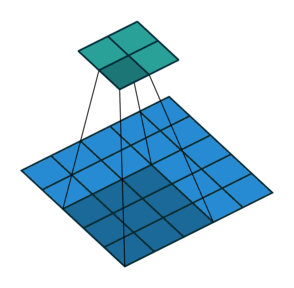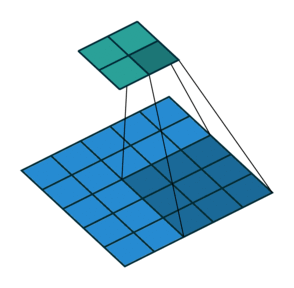 |
 |
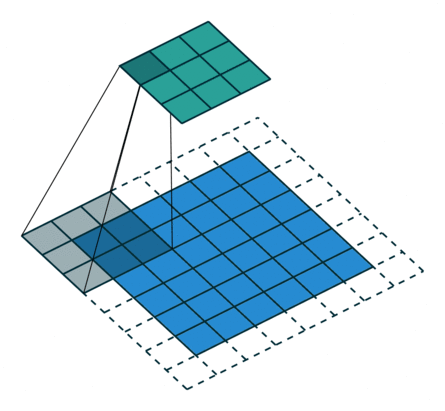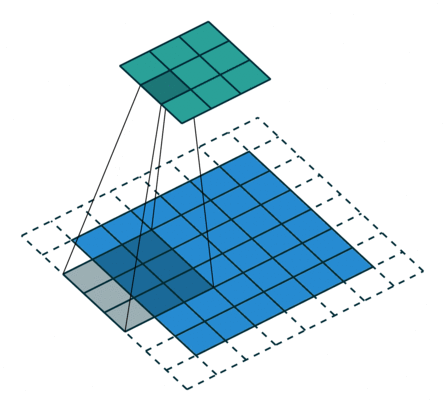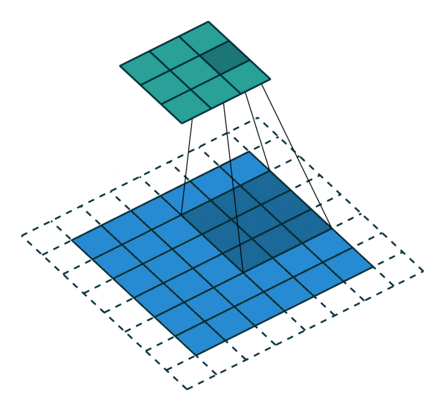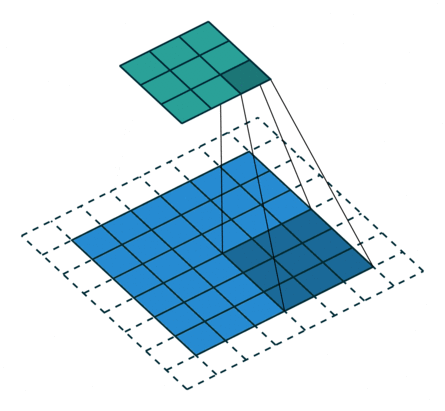 |
|
| No padding, strides | Padding, strides | Padding, strides (odd) | |
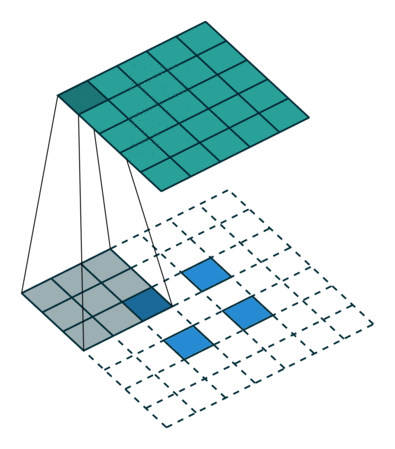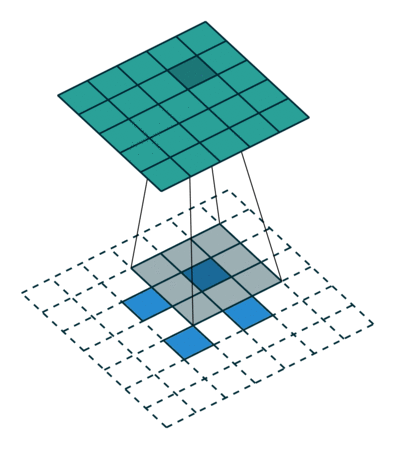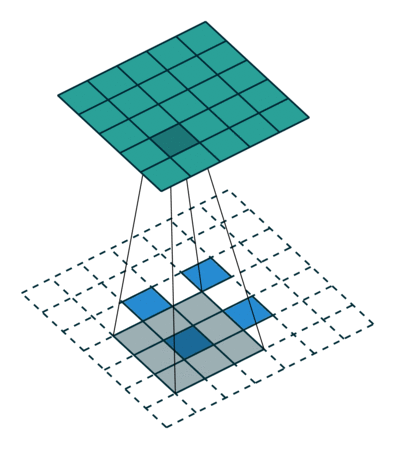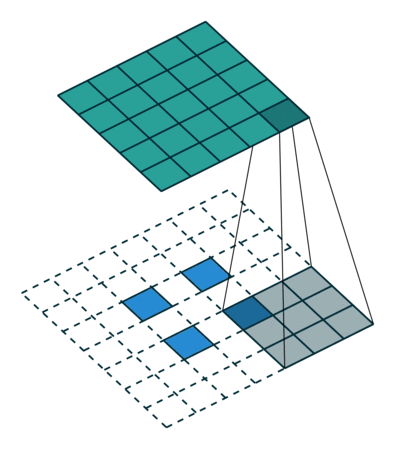 |
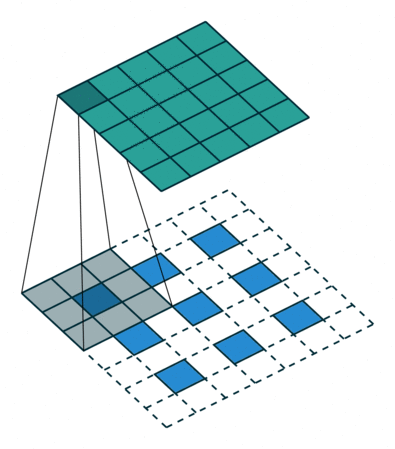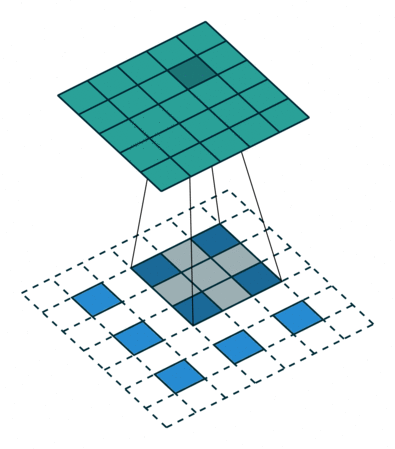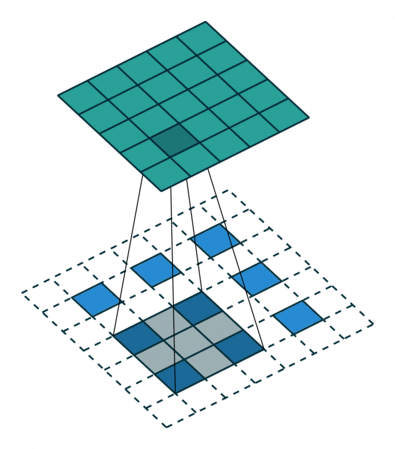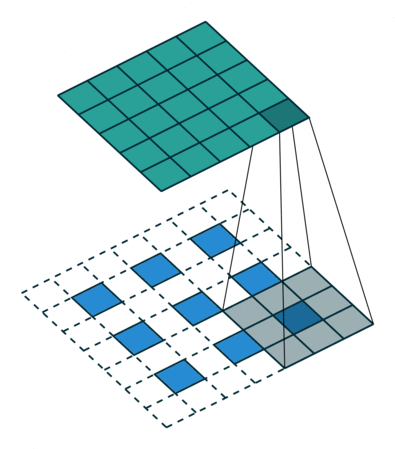 |
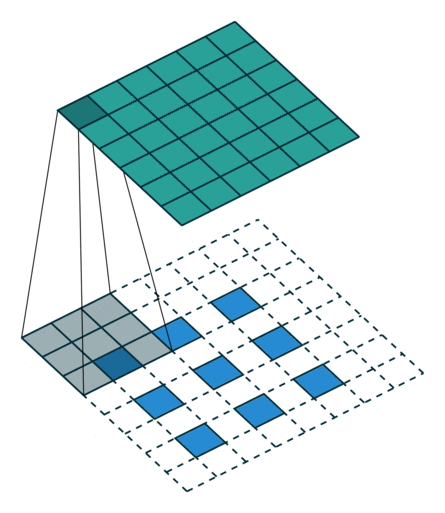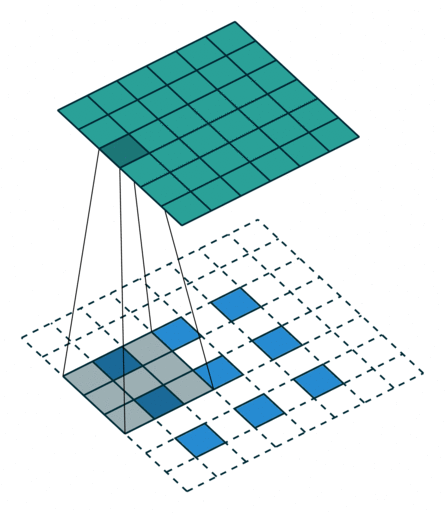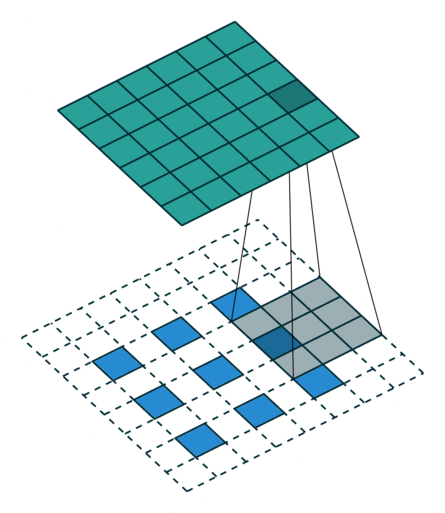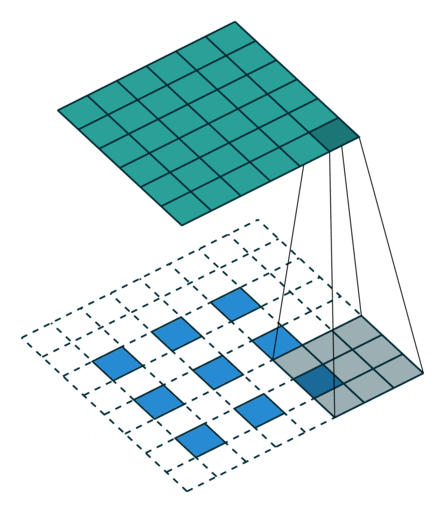 |
|
| No padding, strides, transposed | Padding, strides, transposed | Padding, strides, transposed (odd) | |
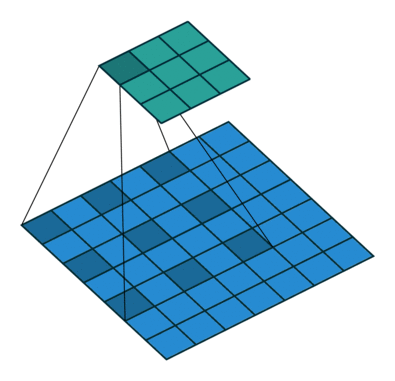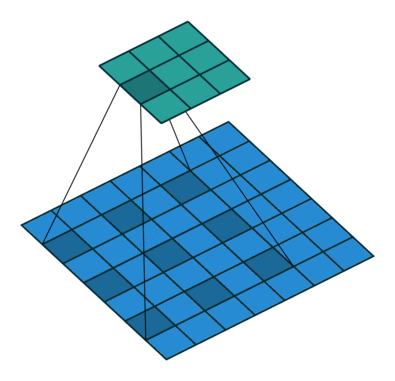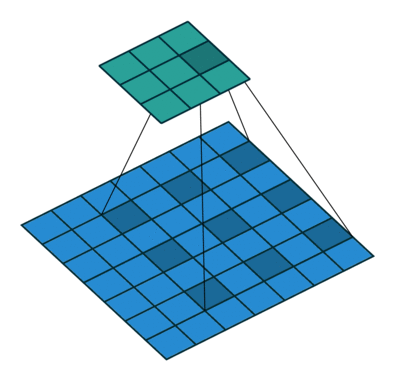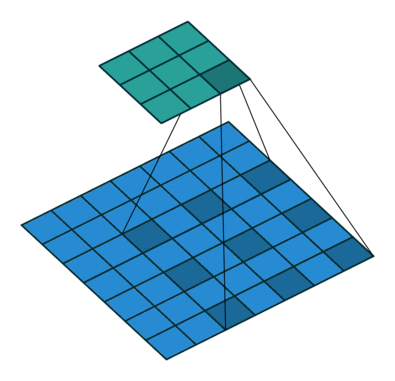 |
|||
| No padding, no stride, dilation |
来源:https://github.com/vdumoulin/conv_arithmetic
形象解释各种卷积算法(Convolution animations)的更多相关文章
- Convolution卷积算法python以numpy,Matplotlib实现
1:简述 Numpy拥有函数numpy.convolve(a, v, mode='full')[source]¶,通过该函数完成卷积算法并图形化(Matplotlib)实现. 2:卷积定理 原理: 设 ...
- 从图(Graph)到图卷积(Graph Convolution):漫谈图神经网络模型 (二)
本文属于图神经网络的系列文章,文章目录如下: 从图(Graph)到图卷积(Graph Convolution):漫谈图神经网络模型 (一) 从图(Graph)到图卷积(Graph Convolutio ...
- 如何直观的解释back propagation算法?
转自:知乎-https://www.zhihu.com/question/27239198 作者:匿名用户链接:https://www.zhihu.com/question/27239198/answ ...
- 从图(Graph)到图卷积(Graph Convolution):漫谈图神经网络模型 (一)
本文属于图神经网络的系列文章,文章目录如下: 从图(Graph)到图卷积(Graph Convolution):漫谈图神经网络模型 (一) 从图(Graph)到图卷积(Graph Convolutio ...
- 卷积神经网络中的Winograd快速卷积算法
目录 写在前面 问题定义 一个例子 F(2, 3) 1D winograd 1D to 2D,F(2, 3) to F(2x2, 3x3) 卷积神经网络中的Winograd 总结 参考 博客:blog ...
- 函数编程中functor和monad的形象解释
函数编程中functor和monad的形象解释 函数编程中Functor函子与Monad是比较难理解的概念,本文使用了形象的图片方式解释了这两个概念,容易理解与学习,分别使用Haskell和Swift ...
- 卷积(convolution)与相关(correlation)(matlab 实现)
1. 卷积(convolution) 输出 y(n) 是作为在 x(k) 和 h(n−k)(反转和移位)重叠之下的样本和求出的. 考虑下面两个序列: x(n)=[3,11,7,0,−1,4,2],−3 ...
- 从图(Graph)到图卷积(Graph Convolution):漫谈图神经网络模型 (三)
本文属于图神经网络的系列文章,文章目录如下: 从图(Graph)到图卷积(Graph Convolution):漫谈图神经网络模型 (一) 从图(Graph)到图卷积(Graph Convolutio ...
- 转置卷积Transposed Convolution
转置卷积Transposed Convolution 我们为卷积神经网络引入的层,包括卷积层和池层,通常会减小输入的宽度和高度,或者保持不变.然而,语义分割和生成对抗网络等应用程序需要预测每个像素的值 ...
随机推荐
- 小小知识点(十八)U盘中病毒了,System Volume Information文件夹删除不掉
win+R调出命令窗口后搜索cmd,启用cmd命令编辑器,并输入以下命令: attrib "H:\System Volume Information" -s //这句话可以选择 ...
- 08_jquery里面的$(this)和this都什么时候用,有什么区别
当你用的是jquery时,就用$(this),如果是JS,就用this $(this).html( $(this).html() + " BAM! "); 这个里的html()是J ...
- LEFT函数使用
详解:LEFT函数用于从一个文本字符串的第一个字符开始返回指定个数的字符 1.提取A2单元格从左往右2位字符 2.函数使用用途: LEFT函数用于从一个文本字符串的第一个字符开始返回指定个数的字符 语 ...
- Centos7 编译安装PHP7
Centos7 编译安装PHP7 编译安装的方式可以让组件等设置更加合理,但需要你对PHP的代码及各种配置非常的熟悉,以下为大致的安装流程,大家可以参考 1.下载编译工具 yum groupinsta ...
- 深入浅出 JVM 系列(一)什么是 JVM?它处于什么位置?
.katex { display: block; text-align: center; white-space: nowrap; } .katex-display > .katex > ...
- 【转】ArcGIS Server 10.1 动态图层—更改风格
在 ArcGIS Server REST API中我们可以通过向Graphicslayer中添加临时图元的方法来完成对显示结果的渲染:如果仅仅是更改原有地图服务显示风格,在ArcGIS10.1下使用动 ...
- Spring Boot从零入门2_核心模块详述和开发环境搭建
目录 1 前言 2 名词术语 3 Spring Boot核心模块 3.1 spring-boot(主模块) 3.2 spring-boot-starters(起步依赖) 3.3 spring-boot ...
- CTPN中anchors代码
import numpy as np def generate_basic_anchors(sizes, base_size=16): #base_anchor([0,0,15,15]) base_a ...
- Java Data类
Date类的概述 java.util,Date 表示日期和时间的类类 Date 表示特定的瞬间,精确到千分之一秒(毫秒) 获取时间原点到当前系统时间经历了多少秒 // 时间原点:1970 年 01 月 ...
- python对象的初始化
效果图: 代码: # 对象的初始化 class Person: # 在类中可以定义一些特殊方法(魔术方法) # 特殊方法都是以__开头,__结尾的方法 前后都是两个下划线 # 特殊方法会在特殊的时刻自 ...
