刷题72. Edit Distance

一、题目说明

题目72. Edit Distance，计算将word1转换为word2最少需要的操作。操作包含：插入一个字符，删除一个字符，替换一个字符。本题难度为Hard！

二、我的解答

这个题目一点思路也没，就直接看答案了。用的还是dp算法，dp[n1+1][n2+1]中的dp[i][j]表示将word1的前i位，变为word2的前j位需要的步骤。注意第1行是空，第1列也是空。

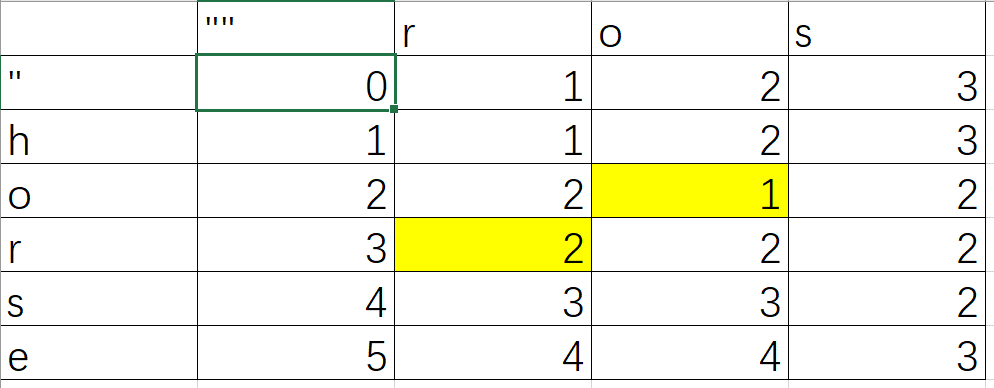
1.第一行中，dp[0][i]表示空字符""到word2[0,...,i]需要编辑几次

2.第一列中，dp[i][0]表示空字符到word2[0,...,i]需要编辑几次

3.循环计算dp的值

if(word1[i]==word2[j]){
    dp[i][j] == dp[i-1][j-1]
}else{
    dp[i][j]=min(dp[i−1][j−1],dp[i][j−1],dp[i−1][j])+1
}

有了方法，实现不难：

class Solution{
	public:
		int minDistance(string word1,string word2){
			int n1 = word1.size(),n2= word2.size();
			if(n1<=0) return n2;
			if(n2<=0) return n1;
			vector<vector<int>> dp(n1+1,vector<int>(n2+1,0));
			//初始化第1行
			for(int i=0;i<=n2;i++){
				dp[0][i] = i;
			}

			//初始化第1列
			for(int i=0;i<=n1;i++){
				dp[i][0] = i;
			}

			//计算dp矩阵
//			if(word1[i]==word2[j]){
//			    dp[i][j] == dp[i-1][j-1]
//			}else{
//			    dp[i][j]=min(dp[i-1][j-1],dp[i][j-1],dp[i-1][j])+1
//			}
			for(int i=1;i<=n1;i++){//行
				for(int j=1;j<=n2;j++){//列
					if(word1[i-1]==word2[j-1]) {
						dp[i][j] = dp[i-1][j-1];
					}else{
						dp[i][j] = min(min(dp[i-1][j],dp[i][j-1]),dp[i-1][j-1])+1;
					}
				}
			}
			return dp[n1][n2];
		}
};

性能如下：

Runtime: 16 ms, faster than 40.38% of C++ online submissions for Edit Distance.
Memory Usage: 11.3 MB, less than 62.50% of C++ online submissions for Edit Distance.

三、优化措施

今天做这么多吧，有点晕了。明天继续！

再回头看看题目Edit Distance，我好像以前做过，不过忘记了。