2018 东北地区大学生程序设计竞赛(ABEHIK)

HDU6500:Problem A. Game with string

题意：

　　给你一个字符串s以及它的m个子串的首尾位置，现在Alice和 Bob两个人轮流在任一子串的前面或者后面加1个字符，要求加了这个串加了一个字符之后仍然是s的子串，谁不能加了谁就输了，要你输出谁赢。

题解：

　　每个子串可以加的字符次数是恒定的：s串的长度－子串的长度。那么我们将所有子串可以加的次数加起来再判断奇偶就能得出答案。

　　傻逼多组WA了几发

代码：

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = +;
const int INF = 1e9+;
const ll mod = ;
int main() {
    string s;
    while (cin>>s){
        int len = s.length();
        int n,l,r,sum = ;
        scanf("%d",&n);
        for (int i = ; i < n; i++){
            scanf("%d%d",&l,&r);
            sum += len - (r-l+);
        }
        if (sum&) printf("Alice\n");
        else printf("Bob\n");
    }
    return ;
}

HDU6501:Problem B. Memory Banks

题意：

　　有60种不同种类的内存存储区，编号为0~59，第i种内存存储区的内存大小为2ⁱ，告诉你每种内存存储区的数量。

　　有n个空间站，每个空间站需要w_i的内存空间，每个空间站你都要用你已有的内存存储区来为它提供正好w_i的内存空间。

　　如果有空间站不能正好有w_i的内存空间输出-1，否则输出你剩下的内存存储区的总存储量。

题解：

　　要使组成的空间站尽可能多，我们需要先取容量大的。我们可以把每个站需要的内存空间转化为2进制，从高位到低位，如果这i位为1就代表需要1个容量为2ⁱ的内存存储区，如果少了可以用2倍的容量为2^i-1的内存存储区代替。

　　例如如果需要10的内存空间，化成2进制就是1010，需要1个2³和1个2¹，若没有容量为2³的可以用两个容量为2²的代替。

　　如果当前空间站内存不够，则输出-1，否则求各个类型剩余容量与个数的乘积之和。

代码：

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = +;
const int INF = 1e9+;
const ll mod = 1e9+;
ll qp(ll a, ll b){
    ll ans = ;
    while (b) {
        if (b&) ans = (ans * a) % mod;
        a = (a * a) % mod;
        b >>= ;
    }
    return ans;
}
ll a[];
int main() {
    while (~scanf("%lld",&a[])) {
        for (int i = ; i < ; i++) scanf("%lld",&a[i]);
        int n;
        scanf("%d",&n);
        bool fg = ;
        while (n--) {
            ll w,sum = ;
            scanf("%lld",&w);
            int cnt = ,b[];
            while (w) {
                b[cnt++] = w%;
                w>>=;
            }
            for (int i = cnt - ; i >= ; i--) {
                sum = sum *  + b[i];
                if (!a[i]) continue;
                if ( sum > a[i]) {
                    sum -= a[i];
                    a[i] = ;
                } else {
                    a[i] -= sum;
                    sum = ;
                }
            }
            if (sum) fg = ;
        }
        if (!fg) printf("-1\n");
        else {
            ll ans = ;
            for (int i = ; i < ; i++) {
                if (a[i]) ans = (ans + (a[i]%mod) * qp(,i) % mod )%mod;
            }
            printf("%lld\n",ans);
        }
    }
    return ;
}

HDU6504:Problem E. Split The Tree

题意：

　　给你一颗节点由1到n编号的树，告诉你每个点的值Wi 。将树的权重定义为树中 不同的节点的值Wi 的数量。

　　删掉一条边之后这棵树就变成了两棵树，得分是两颗数的权重和，要你求一棵树拆成两棵树的最大权重和。

题解：

　　我们可以通过dfs序将这棵树 变成一个线性的，且每个子树在一段连续区间。求树的权重就相当于求一段区间内不同值的数量。

　　要求删掉一条边之后形成的两棵树的最大权重和。我们可以枚举删每一条边时的权重和，

　　在每一次计算的时候，我们可以用树状数组维护，将区间扩大一倍，如果删掉边之后一个子树的区间范围为[l,r] ，那么另一个子树区间为[r+1,n+l-1]。计算这两个区间不同节点值数量和即可。

　　这题也可以用莫队，还没写，待补。

代码：

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N =  +;
const int INF = 1e9+;
const ll mod = 1e9+;
struct node{
    int id,l,r;
    node() {}
    node(int id,int l,int r):id(id),l(l),r(r) {}
} q[N];
int n,dfsnum;
int sum[N], val[N], L[N], R[N], vis[N], ans[N], num[N];
vector<int> edge[N];
bool cmp(node x,node y) {
    if (x.r != y.r) return x.r < y.r;
    else return x.l < y.l;
}
int lowbit(int x) {
    return x&(-x);
}
void add(int x,int k) {
    while (x <= n*) {
        sum[x]+=k;
        x+=lowbit(x);
    }
}
int query(int x) {
    int ans = ;
    while (x) {
        ans += sum[x];
        x -=lowbit(x);
    }
    return ans;
}
void dfs(int x) {
    L[x] = ++dfsnum;
    num[dfsnum] = num[dfsnum+n] = x;
    for (int i = ; i < edge[x].size(); i++) {
        dfs(edge[x][i]);
    }
    R[x] = dfsnum;
}
int main() {
    while(~scanf("%d",&n)) {
        for (int i = ; i <= n; ++i) {
            edge[i].clear();
        }
        for (int i = ; i <= n; i++) {
            int u;
            scanf("%d",&u);
            edge[u].push_back(i);
        }
        dfsnum = ;
        dfs();
        for (int i = ; i <= n; i++) {
            scanf("%d",&val[i]);
            val[n+i] = val[i];
        }
        int cnt = ;
        for (int i = ; i <= n; i++) {
            q[++cnt] = node(i,L[i],R[i]);
            q[++cnt] = node(i,R[i] + , n+L[i]-);
        }
        sort(q+,q++cnt,cmp);
        int maxx = , top = ;
        memset(vis,, sizeof(vis));
        memset(ans,, sizeof(ans));
        memset(sum,,sizeof(sum));
        for (int i  = ; i <= cnt; i++) {
            for (int j = top; j <= q[i].r; ++j) {
                int x = val[num[j]];
                if (vis[x]) add(vis[x],-);
                vis[x] = j;
                add(vis[x],);
            }
            top = q[i].r+;
            ans[q[i].id] += query(q[i].r) - query(q[i].l - );
            maxx = max(maxx,ans[q[i].id]);
        }
        printf("%d\n",maxx);
    }
    return ;
}

树状数组

HDU6507:Problem H. Store The Matrix

题意：

　　给你一个r*c的矩阵M，它可以分解成多个矩阵相乘：M = A1×A2 · · ·×An (n≥1)，每个矩阵Ai的大小为ri*ci。我们通过存这个n个矩阵的元素来存矩阵M，每个矩阵Ai的元素个数为ri*ci，求最少需要存的元素数量。

题解：

　　这题我的理解是：对于一个矩阵M，你要不就不拆，n=1,存的元素数量为r*c。要不就拆成两个矩阵相乘，我们知道要得到r*c的矩阵，需要两个大小分别为r*x，x*c的矩阵相乘，显然当x为矩阵M的秩时最优。

　　所以这是一个求矩阵的秩的模板题。

　　这个题还可以用高斯消元写，待补。

　　参考博客：https://www.cnblogs.com/letlifestop/p/10819422.html

代码：

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = +;
const int INF = 1e9+;
const ll mod = 1e9+;
int a[N][N];
int n,m;
int r() {
    int i=,j=,k,r,u;
    while(i<n&&j<m)
    {
        r=i;
        for(k=i; k<m; k++)
        {
            if(a[k][j])
            {
                r=k;
                break;
            }
        }
        if(a[r][j])
        {
            if(r!=i)
            {
                for(k=; k<=n; k++)
                {
                    swap(a[r][k],a[i][k]);
                }
            }
            for(u=i+; u<m; u++)
            {
                if(a[u][j])
                {
                    for(k=i; k<=n; k++)
                    {
                        a[u][k]^=a[i][k];
                    }
                }
            }
            ++i;
        }
        j++;
    }
    return i;
}
int main() {
    while(~scanf("%d%d",&n,&m)) {
        for (int i = ; i <= n; i++) {
            for (int j = ; j <= m; j++){
                scanf("%d",&a[i][j]);
            }
        }
        printf("%d\n",min(n*m,max(,r())*(n+m)));
    }
    return ;
}

HDU6508:Problem I. Spell Boost

题意：

　　你有n张牌，每张牌需要wi点法力，能给敌人造成xi点伤害。卡牌有两种类型，一种是魔法牌，一种是增幅牌。一张牌可能包含这两种类型。每当你使用一张魔法牌的时候，对于每一张未被使用的增幅牌i需要的法力值wi减1。现在你有W点法力，问能造成的最大的伤害值为多少。

题解：

　　因为魔法牌能降低增幅牌所需的法力值，所以我们可以先按需要值从小到大取魔法牌，然后在从小到大取增幅牌。每件物品只有一件，容量为W，你可以取或者不取，使伤害值最大。类似于背包问题，不过这里的法力值是会减少的。我们可以用dp[i][j][k] 来表示造成的伤害值，i为第i张牌，j为前面使用了多少张增幅牌，k为用了的法力值。因为我们每次选第i张牌都是在前i-1张牌选了之后操作的，我们可以把数组简化成dp[i%2][j][j]，节省空间。

代码：

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = +;
const int INF = 1e9+;
const ll mod = 1e9+;
struct node{
    int w,x,is1,is2;
}a[N];
int dp[][N][N];
bool cmp(node i, node j) {
    if (i.is1 != j.is1) return i.is1 > j.is1;
    if (i.is2 != j.is2) return i.is2 < j.is2;
    return i.w < j.w;
}
int main() {
    int n,m;
    while(~scanf("%d%d",&n,&m)) {
        memset(dp,-,sizeof(dp));
        for (int i = ; i <= n; i++) {
            scanf("%d%d%d%d",&a[i].w,&a[i].x,&a[i].is1,&a[i].is2);
        }
        sort(a+,a+n+,cmp);
        dp[][][]=;
        for (int i = ; i <= n; i++) {
            memset(dp[i%],-,sizeof(dp[i%]));
            for (int j = ; j <= i; j++) {
                for (int k = ; k <= m; k++) {
                    if (dp[(i - ) % ][j][k] == -) continue;
                    dp[i % ][j][k] = max(dp[i % ][j][k], dp[(i - ) % ][j][k]);
                    int u = j + a[i].is1; //判断是不是魔法牌
                    int v = k + max(, a[i].w - j * a[i].is2);//减之前判断需不需要减
                    if (v <= m) {
                        dp[i % ][u][v] = max(dp[i % ][u][v], dp[(i - ) % ][j][k] + a[i].x);
                    }
                }
            }
        }
        int ans = ;
        for (int i = ; i <=n; i++) {
            for (int j = ; j<= m; j++)
                ans = max(ans,dp[n%][i][j]);
        }
        printf("%d\n",ans);
    }
    return ;
}

HDU6510:Problem K. Harbin Sausage

题意：

　　对于下面这个三视图，给你H和R，每单位体积需要花费 3/Pi(圆周率) 问这个几何体花费的总金额。

　　

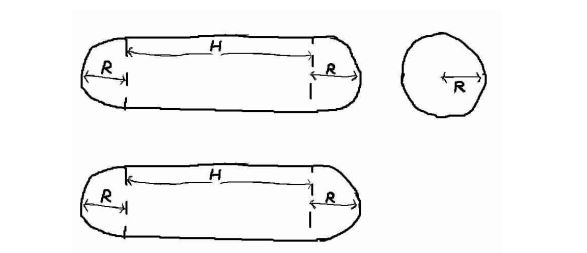
题解：

　　公式为：(4*Pi*R*R*R/3 + Pi*R*R*H) * 3/Pi = 4*R*R*R+3*R*R*H

代码： 

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = +;
const int INF = 1e9+;
const ll mod = ;
int main() {
    int h,r;
    scanf("%d%d",&h,&r);
    printf("%d",*r*r*r+*r*r*h);
    return ;
}