洛谷P1402 酒店之王（网络流）

### 洛谷P1402 题目链接 ###

题目大意：有 n 个人， p 间房间，q 种食物。每个人喜欢一些房间，一些食物，但每间房间、每种食物只能分配给一个人。问最大可以让多少个人满足（当且仅当分配到的房间和食物都是自己喜欢的）。

分析：

1、房间与食物只能被分配一次，被分配后不能再被利用。想到二分图匹配问题。

2、再看题干发现，此题不能直接二分图匹配。因为还需要每个人本身也只能被利用一次。比如某个人喜欢的房间是 1 2 ，食物是 3 4 ，那么即便有 1 - 2 、3 - 4 两种匹配，但也只能满足这一个人，并不是满足了两个人的分配问题。

3、综上，即要保证房间和食物的“流量”最大为1，还需要保证人的“流量”最大为 1 。故可以将房间连接于起点 S ，食物连接于终点 T ，容量为 1 。

按样例来看，图应该为这样：

这样保证了房间和食物只能被用一次，但这建图还是错的。。。因为不能保证 人（点3、点4）的流量最大是 1 。比如：

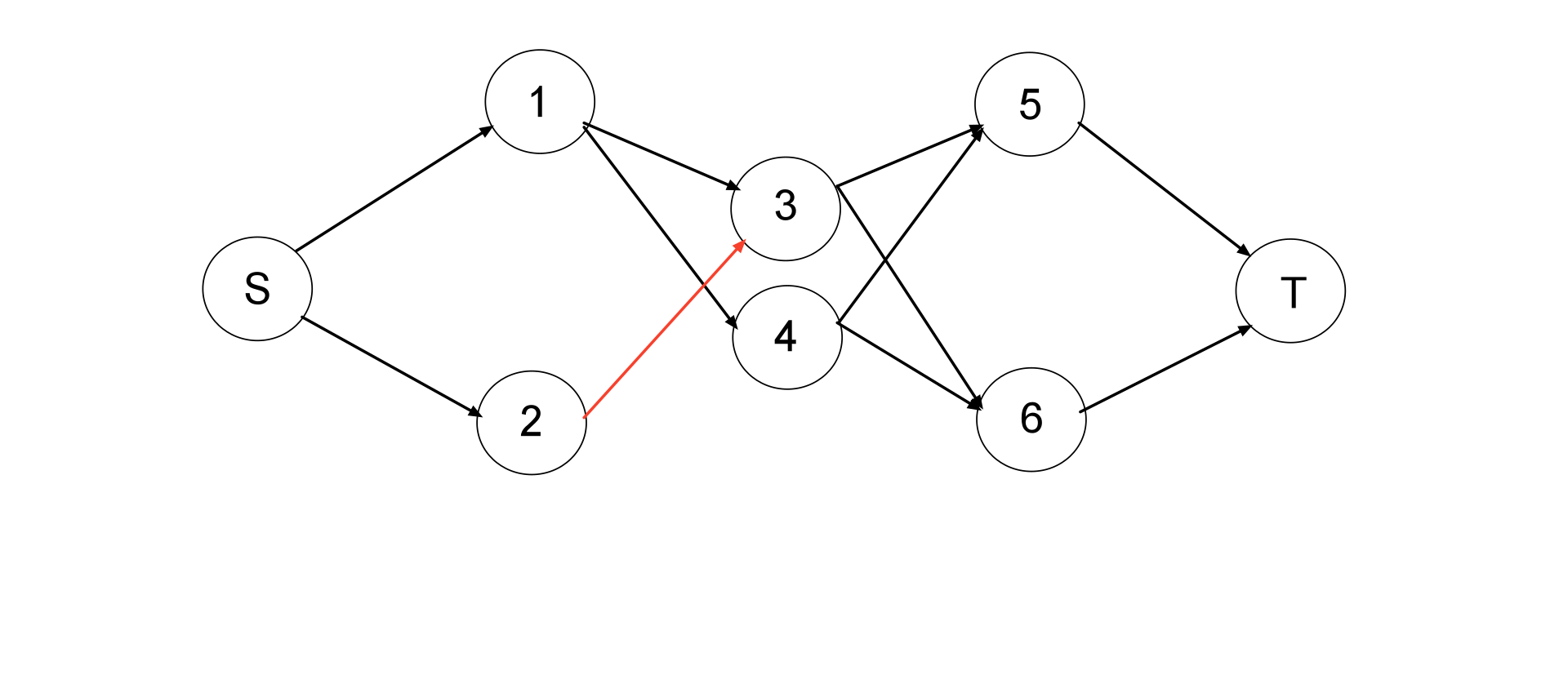
加了这条红色的边后，点3 这个人的最大流量为 2 （从房间 1 和房间 2 流入。且流出于食物 5 和食物 6 ），与题干不符，所以需要把每个人拆成两点，然后中间连一条边，这样就可以限制人的流入与流出了。

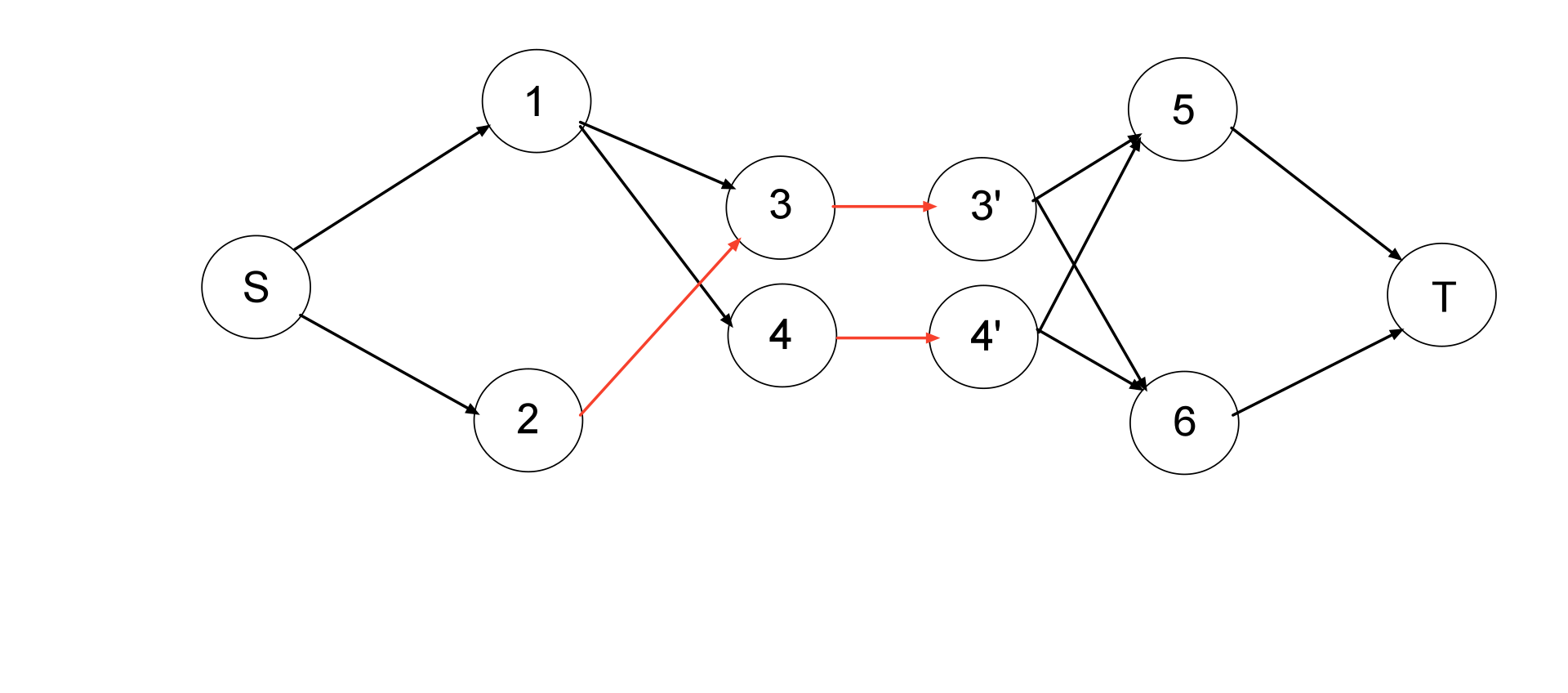
代码如下：

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<queue>
#define maxn 408
#define inf 0x3f3f3f3f
using namespace std;
typedef long long ll;
queue<int> Q;
int n,p,q,cnt,S,T;
int head[maxn],cur[maxn],d[maxn];
struct Edge{
    int to;
    int val;
    int next;
}edge[maxn*maxn];
inline void add(int u,int v,int w){
    edge[++cnt].to=v;
    edge[cnt].val=w;
    edge[cnt].next=head[u];
    head[u]=cnt;
    return;
}
bool bfs(){
    while(!Q.empty()) Q.pop();
    memset(d,-,sizeof(d));
    d[S]=;
    Q.push(S);
    while(!Q.empty()){
        int u=Q.front();
        Q.pop();
        for(int i=head[u];~i;i=edge[i].next){
            int v=edge[i].to;
            if(d[v]==-&&edge[i].val>){
                d[v]=d[u]+;
                Q.push(v);
            }
        }
    }
    return d[T]!=-;
}
int dfs(int u,int flow){
    int nowflow=;
    if(u==T) return flow;
    for(int i=cur[u];~i;i=edge[i].next){
        cur[u]=i;
        int v=edge[i].to;
        if(d[v]==d[u]+&&edge[i].val>){
            if(int k=dfs(v,min(flow-nowflow,edge[i].val))){
                edge[i].val-=k;
                edge[i^].val+=k;
                nowflow+=k;
                if(nowflow==flow) break;
            }
        }
    }
    if(!nowflow) d[u]=-;
    return nowflow;
}
int Dinic(){
    int ans=;
    while(bfs()){
        for(int i=;i<=T;i++) cur[i]=head[i];
        ans+=dfs(S,inf);
    }
    return ans;
}
int main()
{
    scanf("%d%d%d",&n,&p,&q);
    int A;
    cnt=-;
    memset(head,-,sizeof(head));
    S=,T=*n+p+q+;
    for(int i=;i<=p;i++) add(S,i,),add(i,S,);
    for(int i=;i<=q;i++) add(p+*n+i,T,),add(T,p+*n+i,);
    for(int i=;i<=n;i++){
        for(int j=;j<=p;j++){
            scanf("%d",&A);
            if(A) add(j,p+i,),add(p+i,j,);
        }
        add(p+i,p+n+i,),add(p+n+i,p+i,);
    }
    for(int i=;i<=n;i++){
        for(int j=;j<=q;j++){
            scanf("%d",&A);
            if(A) add(p+n+i,p+*n+j,),add(p+*n+j,p+n+i,);
        }
    }
    printf("%d\n",Dinic());
}