HDU 2068 RPG错排 [错排公式]

1.题意：1到N的序列的排列中，元素位置与元素值相对应的情况（值为i的元素在某个排列中正好排在第i个位置）大于等于序列规模一半的情况，有多少个？

2.输入输出：每组数据一个数，N，规定输入以0结尾；

3.分析：原题意换句话说，就是针对1到N的全排列，错排元素的个数小于等于N的情况有多少；

那么，输出即为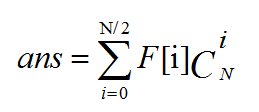：    ，其中F[i]表示1到i的错排方案数，后面一项为组合数，即选取i个错排；

这里推导一下错排公式，F[N]表示1到N的错排方案；第一步:选取N放到1到N-1之中任意一个位置，这样就有N-1种放法；第二步：分两种情况，不妨设第一步被N占据的位置为K，当位置N放置的数恰巧为K时，此时就相当于,K,N交换位置了，对应的错排方案为F[N-2];当位置N放置的数不为K时，此时的情况：1到K-1，K+1到N的位置要错排放置1到N-1的元素，N-1个 位置，N-1个元素，与F[N-1]的情况相比，只是多了一组（数K与位置N）的对应，而且这里N不放置K，就等效于普通的情况下（数K与位置K）的错排情况；举个例子，位置12345，数12345，现在5放置在2的位置上，剩下数1234，位置1345，且位置5上不放2，这里和1234-1234的错排有什么区别么？把位置5当成位置2，反正也是2不放在位置5上，与1234-1234里2不放在位置2上等效；综上所述，错排公式为F[i]=(i-1)*(F[i-1]+F[i-2]),其中，F[1]=0，F[2]=1；

 # include <iostream>
 # include <cstdio>
 using namespace std;
 const int MAXN=;
 int dp[MAXN];
 int N;
 long long Cn(int n,int m)
 {
     if(n==) return ;
     n=m-n>n?n:m-n;
     long long up,down;
     up=down=;
     for(int i=;i<=n;i++)
     {
         up*=m-i+;
         down*=i;
     }
     long long res=up/down;
     return res;
 }
 void Init()
 {
     dp[]=;
     dp[]=;
     dp[]=;
     for(int i=;i<;i++)
         dp[i]=(i-)*(dp[i-]+dp[i-]);
 }
 int main()
 {
     Init();
     while(scanf("%d",&N)!=EOF)
     {
         if(N==) break;
         long long res=;
         for(int i=;i<=N/;i++)
             res+=dp[i]*Cn(i,N);
         printf("%lld\n",res);
     }
     return ;
 }