机器学习理论基础学习5--- PCA

一、预备知识

减少过拟合的方法有：(1)增加数据 （2）正则化（3）降维

维度灾难：从几何角度看会导致数据的稀疏性

举例1：正方形中有一个内切圆，当维度D趋近于无穷大时，圆内的数据几乎为0，所有的数据集中于球外(空壳)

举例2：圆内有个内圆，当维度D趋近于无穷大时，环形内的数据与外圆的数据比为1，说明所有的数据集中于环中(空壳)

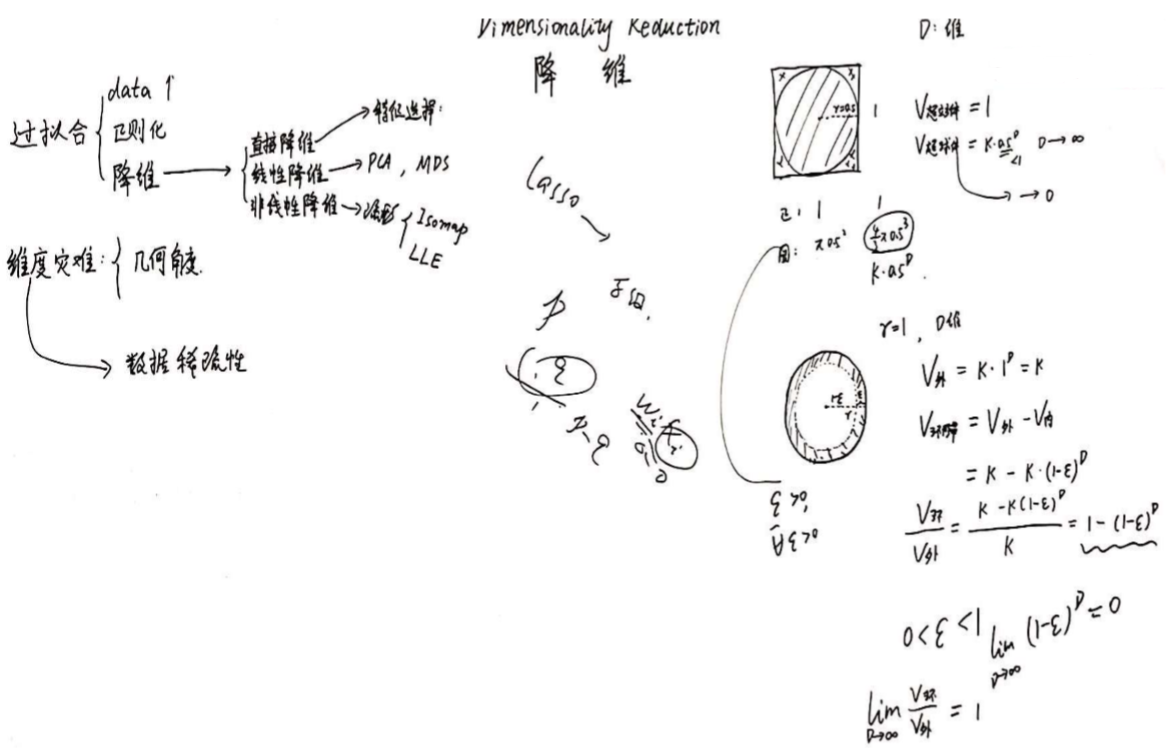
样本均值 & 样本方差的矩阵表示

二、PCA：一个中心 + 两个基本点（最大投影方差、最小重构距离）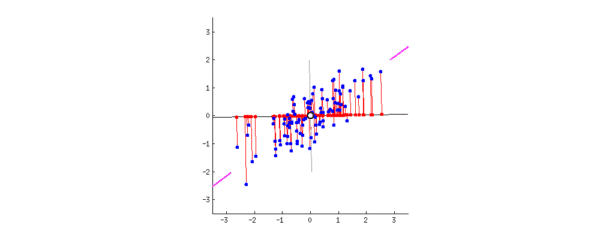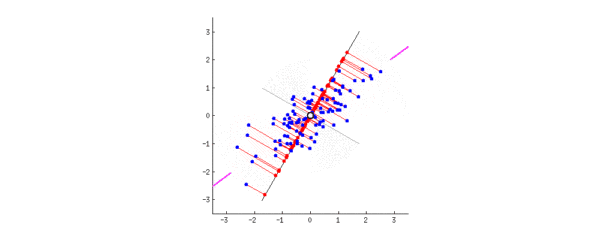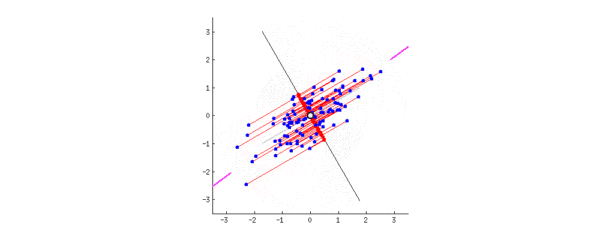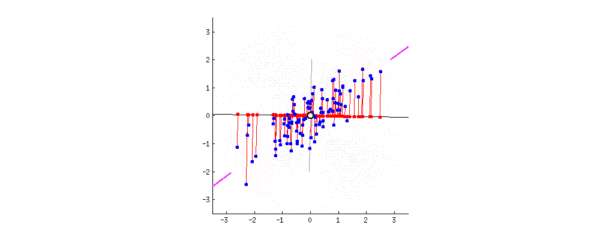

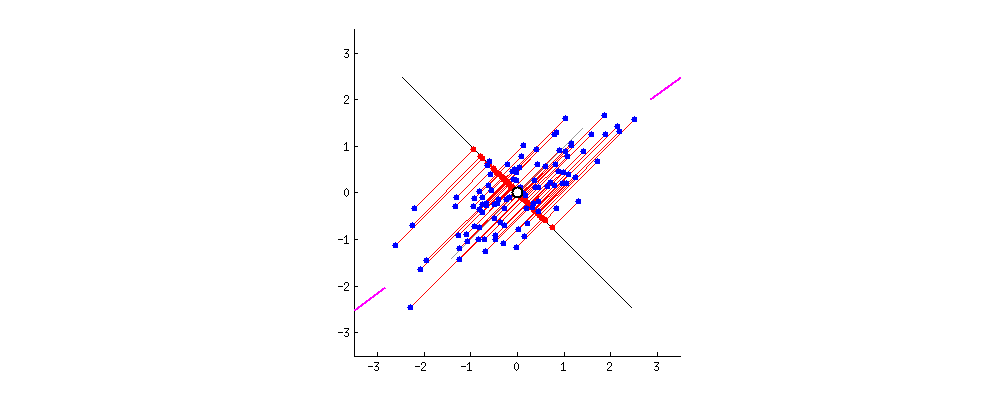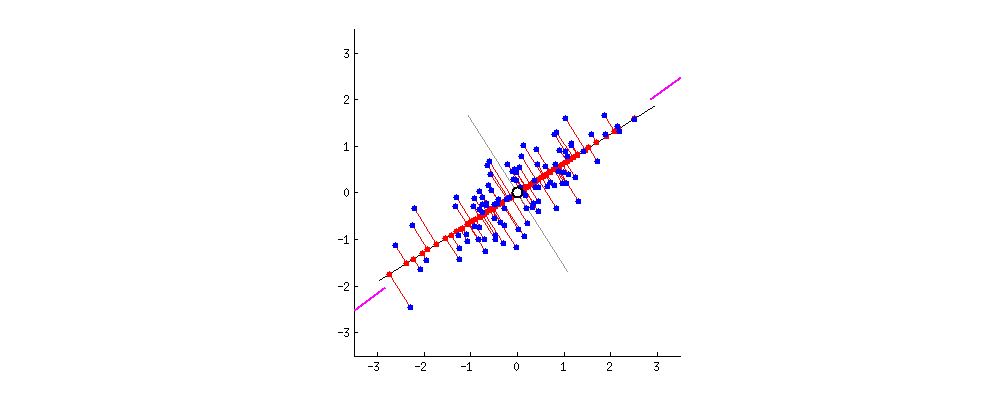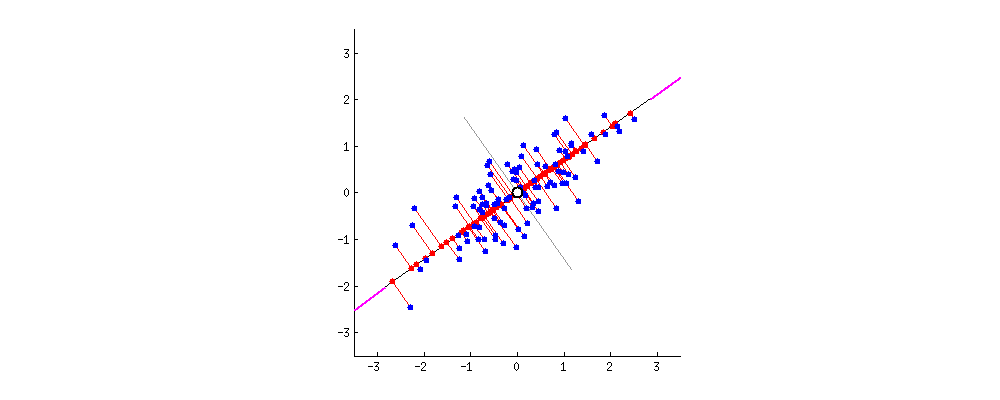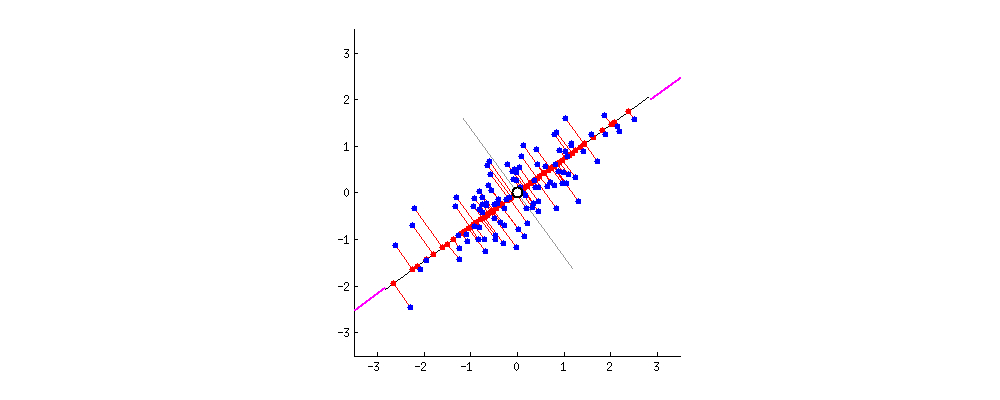
1、最大投影方差角度

2、最小重构代价角度

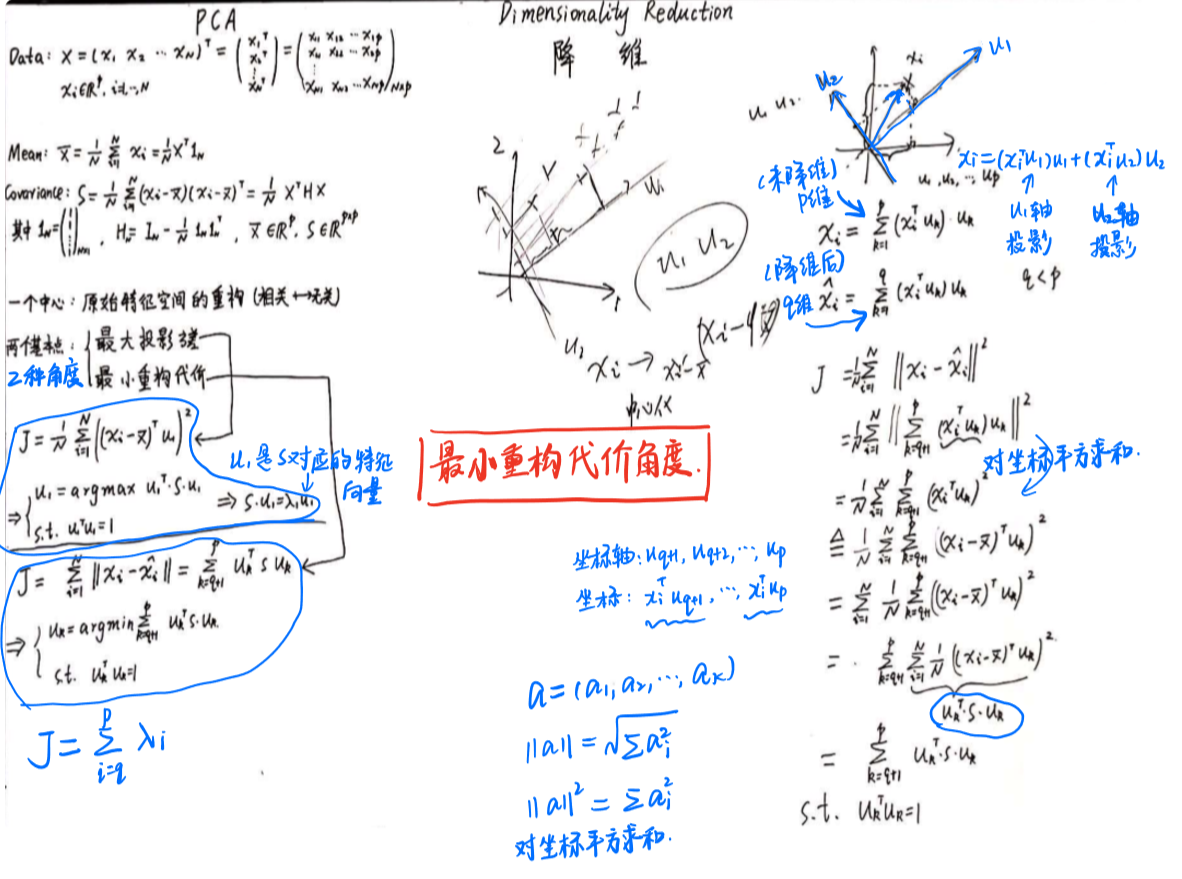
3、SVD角度

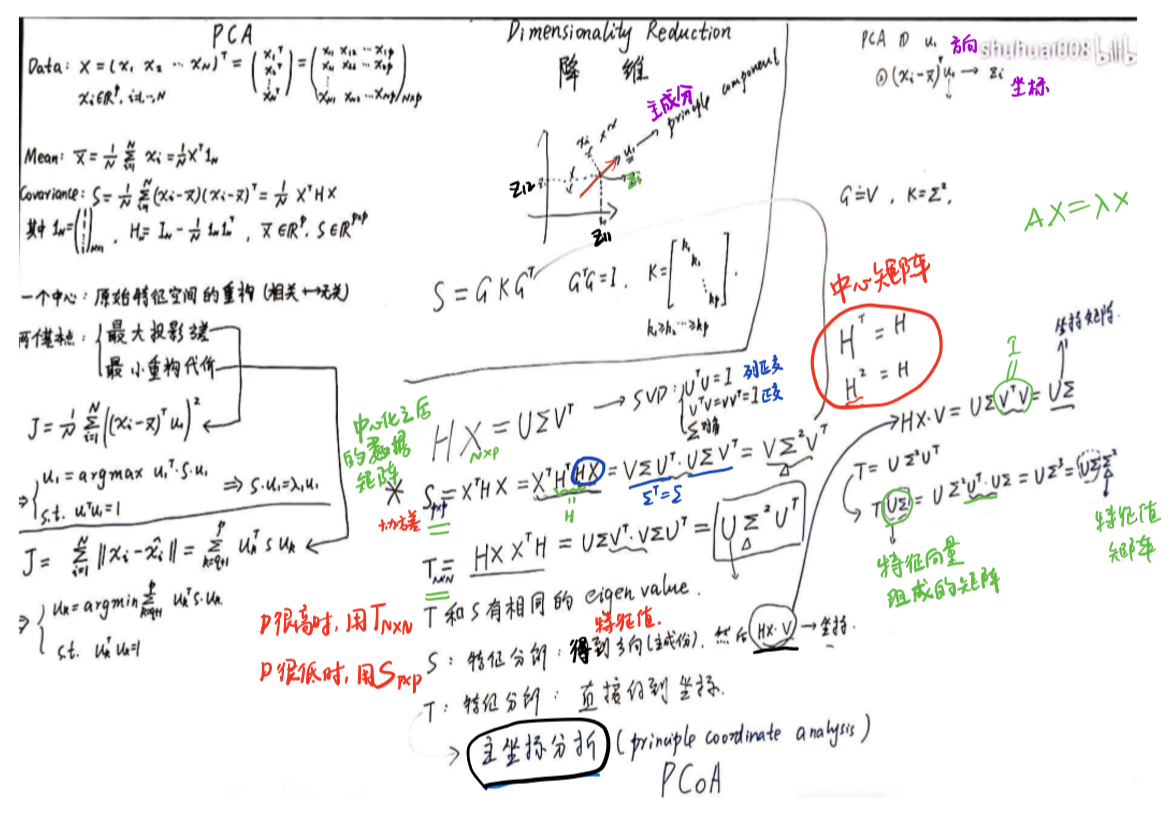
主成分分析（PCA）：先得到方向（主成分），再得到坐标

主坐标分析（PCoA）：直接得到坐标

4、概率角度（probabilistic PCA，P-PCA）

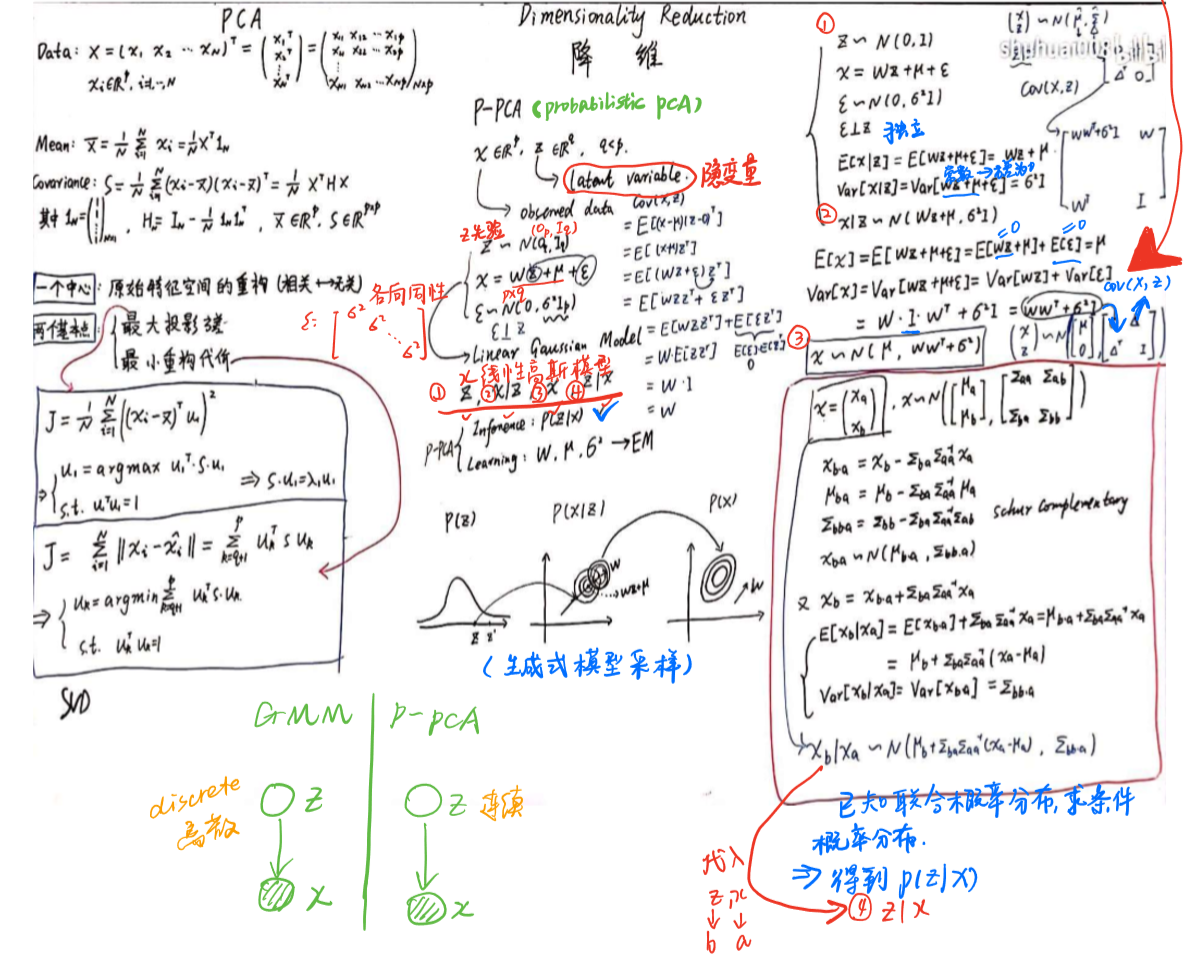
 GMM与P-PCA的区别在于，GMM的隐变量是离散的，而P-PCA的隐变量是连续的。

5、PCA算法总结

这里对PCA算法做一个总结。作为一个非监督学习的降维方法，它只需要特征值分解，就可以对数据进行压缩，去噪。因此在实际场景应用很广泛。为了克服PCA的一些缺点，出现了很多PCA的变种，比如为解决非线性降维的KPCA，还有解决内存限制的增量PCA方法Incremental PCA，以及解决稀疏数据降维的PCA方法Sparse PCA等。

PCA算法的主要优点有：

• 仅仅需要以方差衡量信息量，不受数据集以外的因素影响。　
• 各主成分之间正交，可消除原始数据成分间的相互影响的因素。
• 计算方法简单，主要运算是特征值分解，易于实现。

PCA算法的主要缺点有：

• 主成分各个特征维度的含义具有一定的模糊性，不如原始样本特征的解释性强。
• 方差小的非主成分也可能含有对样本差异的重要信息，因降维丢弃可能对后续数据处理有影响。

参考文献：

【1】机器学习(28)【降维】之sklearn中PCA库讲解与实战

【2】PCA的数学原理

【3】PCA主成分分析学习总结