SVM 推到期间 遇到的 表背景知识 （间隔最大化）

背景，在看原理的时候，发现很多地方一知半解的，补充如下。

其他补充：

注：以下的默认为2分类

1、SVM原理：

(1)输入空间到特征空间得映射

所谓输入空间即是输入样本集合，有部分情况输入空间与特征空间是相同得，有一部分情况二者是不同的，而模型定义都是定义到特征空间的，特征空间是指所有的输入特征向量，特征向量是利用数值来表示的n维向量，输入空间到特征空间的映射，也就是对所用的特征进行数值量化（本人这么理解），与概率中的随机变量是一样的形式，随机变量是由样本空间到实数集的映射，例如：抛硬币的样本空间是{正面，反面}，映射到实数集便为{1,0}

(2)求得间隔最大化最优分离超平面

所谓分离超平面，即是能够将所有的特征向量划分为两类的平面或直线(特征有两个变为直线，多个变为平面，即几维的问题)，比如二维的情况下，一条线，能够坐标系中的所有点划分为两类，最优意为可以将所有的点尽量进行正确的划分，间隔最大化意为：在两类区域中各自距离直线最近的点到直线的距离是最大的，因此可以求得唯一的间隔最大化最优分离超平面w*x+b*=0,由于是距离因此是由法向量和截距决定，w*为法向量，b*为截距，此处对这个方程进行解释：法向量是从点到平面的垂直方向，在几何中求平面的方程时，平面方程可以设为一般方程Ax+By+Cz+D=0,这便可以看作为(A,B,C)*(x,y,z)即w*=(A,B,C),特征向量x=(x,y,z),b*=D.同理在求直线直线可设为Ax+By+C=0，因此求超平面时即为求w*,b*.

(3)求分类决策函数

所谓分类决策函数只是一个符号函数f(x)=sign(w*x+b*),sign是一个符号函数,取输入值的符号（正负），在上边取得法向量和截距以后与输入特征向量运算后将结果带入sign()得到分类

2、基础概念

(1)函数间隔

上边已经说了是求到超平面的最近距离的点的距离最大的超平面，因此求距离是很重要的一步，根据点到平面的距离公式分子为|w*x+b|,由于分母是相同的，所以|w*x+b|可以相对的表示出距离的大小。y（向量）在此表示的是每个特征向量的分类，而由上边已经知道，分类决策是求的符号的，因此可以确定w*x+b与y的符号（相对应元素）是相同的，因此可以利用y(w*x+b)来表示分类的正确性和确信度，这就是函数间隔:　　　　　　　　　　　　　　　　　　　　　　　　　　

注：超平面关于特征空间的函数间隔是值所有特征向量到超平面的函数间隔中的最小值

　　　　　　　　　　　　　　　　　　　　　　　　　　

(2)几何间隔

利用函数间隔来具体衡量时，会出现一个问题，当法向量和截距同时扩大两倍时，超平面不变，但是函数间隔却便为原来的两倍，因此引入几何间隔的概念，其实简单的来说，几何间隔便是函数间隔除以法向量的模，具体公式如下：

　　　　　　　　　　　　　　　　　　　　　　　　　　　　

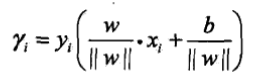
同时由超平面关于特征空间的几何间隔是所有特征向量到超平面的几何间隔中的最小值

　　　　　　　　　　　　　　　　　　　　　　　　　　

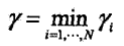
(3)支持向量

在线性可分的情况下，特征空间中距离分离超平面的距离最近的特征向量为支持向量

上面一段话来着：https://www.cnblogs.com/fantasy01/p/4633557.html