HDU 5936 Difference（折半搜索（中途相遇法））

http://acm.hdu.edu.cn/showproblem.php?pid=5936

题意：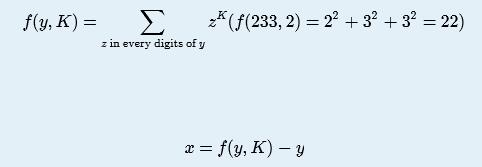

定义了这样一种算法，现在给出x和k的值，问有多少个y是符合条件的。

思路：

y最多只有10位，再多x就是负的了。

这样的话可以将y分为前后两部分，我们先枚举后5位的情况，然后再枚举前5位的情况，通过二分查找找到匹配的项，这样就大大的降低了时间复杂度。

 #include<iostream>
 #include<algorithm>
 #include<cstring>
 #include<cstdio>
 #include<vector>
 #include<stack>
 #include<queue>
 #include<cmath>
 #include<map>
 #include<set>
 using namespace std;
 typedef long long ll;
 const int INF = 0x3f3f3f3f;
 const int maxn=+;

 int p[][];
 int sum[maxn];
 int num[maxn];
 int x, k,cnt;

 void init()  //处于后5位的情况，i是枚举，sum[i]存储的是对应k下的值
 {
     cnt=;
     memset(sum,,sizeof(sum));
     for(int i=;i<;i++)
     {
         int tmp=i;
         while(tmp)
         {
             sum[i]+=p[tmp%][k];
             tmp/=;
         }
         num[cnt++]=sum[i]-i;
     }
     sort(num,num+cnt);
 }

 void solve()  //枚举前5位的值，然后二分查找即可
 {
     ll ans=;
     for(int i=;i<;i++)
     {
         ll tmp=sum[i]-(ll)i*;
         int idx=lower_bound(num,num+cnt,x-tmp)-num;
         while(num[idx]==x-tmp && idx<cnt)
         {
             ans++;
             idx++;
         }
     }
     printf("%lld\n",ans);
 }

 int main()
 {
     //freopen("in.txt","r",stdin);
     for(int i=;i<;i++)   //预处理i^j的值
     {
         p[i][]=;
         for(int j=;j<;j++)
             p[i][j]=p[i][j-]*i;
     }
     int T;
     int kase=;
     scanf("%d",&T);
     while(T--)
     {
         printf("Case #%d: ",++kase);
         scanf("%d%d",&x,&k);
         init();
         solve();
     }
     return ;
 }