OpenCV学习(18) 细化算法(6)
本章我们在学习一下基于索引表的细化算法。
假设要处理的图像为二值图,前景值为1,背景值为0。
索引表细化算法使用下面的8邻域表示法:

一个像素的8邻域,我们可以用8位二进制表示,比如下面的8邻域,表示为00111000=0x38=56
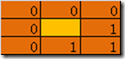
我们可以枚举出各种情况下,当前像素能否删除的表,该表大小为256。它的索引即为8邻域表示的值,表中存的值为0或1,0表示当前像素不能删除,1表示可以删除。deletemark[256]
比如下图第一个表示,索引值为0,它表示孤立点,不能删除,所以deletemark[0]=0,第二个表示索引值为17,它表示端点,也不能删除,所以deletemark[17]=0,第三个表示索引为21,删除的话会改变连通域数量,所以deletemark[21]=0,第四个表示索引值为96,此时可以删除,所以deletemark[96]=1。

最终我们会定义一张完整的表来表示当前像素能否删除。
索引表细化算法描述很简单。
1.找到轮廓,其值用4表示
2.查找值为4的轮廓,查找索引表判断能否删除,能删除的话把它置为0。
循环迭代1,2直到再也没有可以删除的点为止。
下面的算法的代码:
void gThin::cvidxThin1(cv::Mat& src, cv::Mat& dst)
{ if(src.type()!=CV_8UC1)
{
printf("只能处理二值或灰度图像\n");
return;
}
//非原地操作时候,copy src到dst
if(dst.data!=src.data)
{
src.copyTo(dst);
} // P0 P1 P2
// P7 P3
// P6 P5 P4
unsigned char deletemark[256] = {
0,0,0,0,0,0,0,1, 0,0,1,1,0,0,1,1,
0,0,0,0,0,0,0,0, 0,0,1,1,1,0,1,1,
0,0,0,0,0,0,0,0, 1,0,0,0,1,0,1,1,
0,0,0,0,0,0,0,0, 1,0,1,1,1,0,1,1,
0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0, 1,0,0,0,1,0,1,1,
1,0,0,0,0,0,0,0, 1,0,1,1,1,0,1,1,
0,0,1,1,0,0,1,1, 0,0,0,1,0,0,1,1,
0,0,0,0,0,0,0,0, 0,0,0,1,0,0,1,1,
1,1,0,1,0,0,0,1, 0,0,0,0,0,0,0,0,
1,1,0,1,0,0,0,1, 1,1,0,0,1,0,0,0,
0,1,1,1,0,0,1,1, 0,0,0,1,0,0,1,1,
0,0,0,0,0,0,0,0, 0,0,0,0,0,1,1,1,
1,1,1,1,0,0,1,1, 1,1,0,0,1,1,0,0,
1,1,1,1,0,0,1,1, 1,1,0,0,1,1,0,0
};//索引
int i, j;
int width, height;
//之所以减1,是方便处理8邻域,防止越界
width = src.cols -1;
height = src.rows -1;
int step = src.step;
int p0, p1, p2,p3,p4,p5,p6,p7;
uchar* img;
bool ifEnd;
bool border = false; //交换删除的次序,防止从一边细化
while(1)
{ border = !border;
img = dst.data;
for(i = 1; i < height; i++)
{
img += step;
for(j =1; j<width; j++)
{
uchar* p = img + j;
//如果p点是背景点,继续循环
if(p[0]==0) continue;
p0 = p[-step-1]>0?1:0;
p1 = p[-step]>0?1:0;
p2 = p[-step+1]>0?1:0;
p3 = p[1]>0?1:0;
p4 = p[step+1]>0?1:0;
p5 = p[step]>0?1:0;
p6 = p[step-1]>0?1:0;
p7 = p[-1]>0?1:0; //如果sum等于0,则不是内部点,是轮廓点,设置其像素值为2
int sum;
sum = p0 & p1 & p2 & p3 & p4 & p5 & p6 & p7; //判断是否是邻接点或孤立点,0,1分别对于那个孤立点和端点
if(sum==0)
{
dst.at<uchar>(i,j) = 4; //满足删除条件,设置当前像素为0
} }
}
//printf("\n");
//PrintMat(dst);
//执行删除操作
ifEnd = false; img = dst.data;
for(i = 1; i < height; i++)
{
img += step;
for(j =1; j<width; j++)
{
uchar* p = img + j;
//如果p点是背景点,继续循环
if(p[0]!=4) continue;
p0 = p[-step-1]>0?1:0;
p1 = p[-step]>0?1:0;
p2 = p[-step+1]>0?1:0;
p3 = p[1]>0?1:0;
p4 = p[step+1]>0?1:0;
p5 = p[step]>0?1:0;
p6 = p[step-1]>0?1:0;
p7 = p[-1]>0?1:0; p1 = p1<<1;
p2 = p2<<2;
p3 = p3 <<3;
p4 = p4<<4;
p5 = p5<<5;
p6 = p6 <<6;
p7 = p7 << 7; //求的8邻域在索引表中的索引
int sum;
sum = p0 | p1 | p2 | p3 | p4 | p5 | p6 | p7; //判断是否是邻接点或孤立点,0,1分别对于那个孤立点和端点
if(deletemark[sum] == 1)
{
dst.at<uchar>(i,j) = 0; //满足删除条件,设置当前像素为0
ifEnd = true;
} }
} //printf("\n");
//PrintMat(dst);
//printf("\n"); //已经没有可以细化的像素了,则退出迭代
if(!ifEnd) break;
}
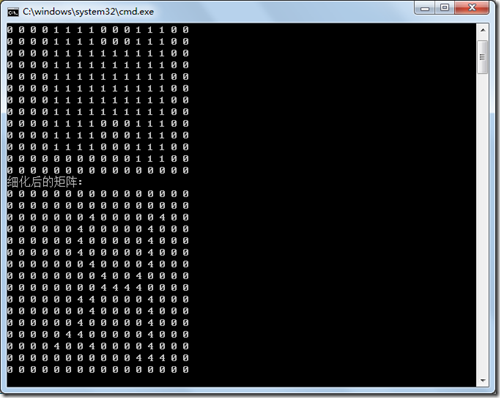
上面的算法可以看到细化后的轮廓偏右了,我们可以更改删除的循环条件,把循环拆分成三个,修改后的代码如下:
void gThin::cvidxThin(cv::Mat& src, cv::Mat& dst)
{ if(src.type()!=CV_8UC1)
{
printf("只能处理二值或灰度图像\n");
return;
}
//非原地操作时候,copy src到dst
if(dst.data!=src.data)
{
src.copyTo(dst);
} // P0 P1 P2
// P7 P3
// P6 P5 P4
unsigned char deletemark[256] = {
0,0,0,0,0,0,0,1, 0,0,1,1,0,0,1,1,
0,0,0,0,0,0,0,0, 0,0,1,1,1,0,1,1,
0,0,0,0,0,0,0,0, 1,0,0,0,1,0,1,1,
0,0,0,0,0,0,0,0, 1,0,1,1,1,0,1,1,
0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0, 1,0,0,0,1,0,1,1,
1,0,0,0,0,0,0,0, 1,0,1,1,1,0,1,1,
0,0,1,1,0,0,1,1, 0,0,0,1,0,0,1,1,
0,0,0,0,0,0,0,0, 0,0,0,1,0,0,1,1,
1,1,0,1,0,0,0,1, 0,0,0,0,0,0,0,0,
1,1,0,1,0,0,0,1, 1,1,0,0,1,0,0,0,
0,1,1,1,0,0,1,1, 0,0,0,1,0,0,1,1,
0,0,0,0,0,0,0,0, 0,0,0,0,0,1,1,1,
1,1,1,1,0,0,1,1, 1,1,0,0,1,1,0,0,
1,1,1,1,0,0,1,1, 1,1,0,0,1,1,0,0
};//索引
int i, j;
int width, height;
//之所以减1,是方便处理8邻域,防止越界
width = src.cols -1;
height = src.rows -1;
int step = src.step;
int p0, p1, p2,p3,p4,p5,p6,p7;
uchar* img;
bool ifEnd;
bool border = false; //交换删除的次序,防止从一边细化
while(1)
{ border = !border;
img = dst.data;
for(i = 1; i < height; i++)
{
img += step;
for(j =1; j<width; j++)
{
uchar* p = img + j;
//如果p点是背景点,继续循环
if(p[0]==0) continue;
p0 = p[-step-1]>0?1:0;
p1 = p[-step]>0?1:0;
p2 = p[-step+1]>0?1:0;
p3 = p[1]>0?1:0;
p4 = p[step+1]>0?1:0;
p5 = p[step]>0?1:0;
p6 = p[step-1]>0?1:0;
p7 = p[-1]>0?1:0; //如果sum等于0,则不是内部点,是轮廓点,设置其像素值为2
int sum;
sum = p0 & p1 & p2 & p3 & p4 & p5 & p6 & p7; //判断是否是邻接点或孤立点,0,1分别对于那个孤立点和端点
if(sum==0)
{
dst.at<uchar>(i,j) = 4; //满足删除条件,设置当前像素为0
} }
}
//printf("\n");
//PrintMat(dst);
//执行删除操作
ifEnd = false; img = dst.data;
for(i = 1; i < height; i++)
{
img += step;
for(j =1; j<width; j+=3)
{
uchar* p = img + j;
//如果p点是背景点,继续循环
if(p[0]!=4) continue;
p0 = p[-step-1]>0?1:0;
p1 = p[-step]>0?1:0;
p2 = p[-step+1]>0?1:0;
p3 = p[1]>0?1:0;
p4 = p[step+1]>0?1:0;
p5 = p[step]>0?1:0;
p6 = p[step-1]>0?1:0;
p7 = p[-1]>0?1:0; p1 = p1<<1;
p2 = p2<<2;
p3 = p3 <<3;
p4 = p4<<4;
p5 = p5<<5;
p6 = p6 <<6;
p7 = p7 << 7; //求的8邻域在索引表中的索引
int sum;
sum = p0 | p1 | p2 | p3 | p4 | p5 | p6 | p7; //判断是否是邻接点或孤立点,0,1分别对于那个孤立点和端点
if(deletemark[sum] == 1)
{
dst.at<uchar>(i,j) = 0; //满足删除条件,设置当前像素为0
ifEnd = true;
} }
} img = dst.data;
for(i = 1; i < height; i++)
{
img += step;
for(j =2; j<width; j+=3)
{
uchar* p = img + j;
//如果p点是背景点,继续循环
if(p[0]!=4) continue;
p0 = p[-step-1]>0?1:0;
p1 = p[-step]>0?1:0;
p2 = p[-step+1]>0?1:0;
p3 = p[1]>0?1:0;
p4 = p[step+1]>0?1:0;
p5 = p[step]>0?1:0;
p6 = p[step-1]>0?1:0;
p7 = p[-1]>0?1:0; p1 = p1<<1;
p2 = p2<<2;
p3 = p3 <<3;
p4 = p4<<4;
p5 = p5<<5;
p6 = p6 <<6;
p7 = p7 << 7; //求的8邻域在索引表中的索引
int sum;
sum = p0 | p1 | p2 | p3 | p4 | p5 | p6 | p7; //判断是否是邻接点或孤立点,0,1分别对于那个孤立点和端点
if(deletemark[sum] == 1)
{
dst.at<uchar>(i,j) = 0; //满足删除条件,设置当前像素为0
ifEnd = true;
} }
} img = dst.data;
for(i = 1; i < height; i++)
{
img += step;
for(j =3; j<width; j+=3)
{
uchar* p = img + j;
//如果p点是背景点,继续循环
if(p[0]!=4) continue;
p0 = p[-step-1]>0?1:0;
p1 = p[-step]>0?1:0;
p2 = p[-step+1]>0?1:0;
p3 = p[1]>0?1:0;
p4 = p[step+1]>0?1:0;
p5 = p[step]>0?1:0;
p6 = p[step-1]>0?1:0;
p7 = p[-1]>0?1:0; p1 = p1<<1;
p2 = p2<<2;
p3 = p3 <<3;
p4 = p4<<4;
p5 = p5<<5;
p6 = p6 <<6;
p7 = p7 << 7; //求的8邻域在索引表中的索引
int sum;
sum = p0 | p1 | p2 | p3 | p4 | p5 | p6 | p7; //判断是否是邻接点或孤立点,0,1分别对于那个孤立点和端点
if(deletemark[sum] == 1)
{
dst.at<uchar>(i,j) = 0; //满足删除条件,设置当前像素为0
ifEnd = true;
} }
} //printf("\n");
//PrintMat(dst);
//printf("\n"); //已经没有可以细化的像素了,则退出迭代
if(!ifEnd) break;
} }
修改后的结果:
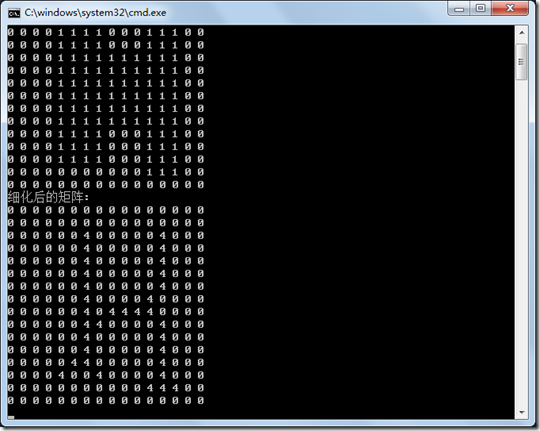
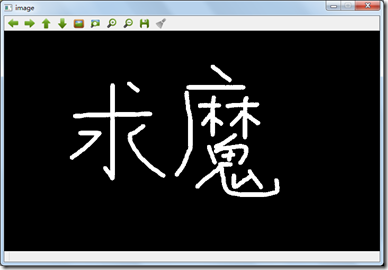
程序源代码:工程FirstOpenCV11
OpenCV学习(18) 细化算法(6)的更多相关文章
- OpenCV学习(16) 细化算法(4)
本章我们学习Rosenfeld细化算法,参考资料:http://yunpan.cn/QGRjHbkLBzCrn 在开始学习算法之前,我们先看下连通分量,以及4连通性,8连通性的概念: http://w ...
- OpenCV学习(15) 细化算法(3)
本章我们学习一下Hilditch算法的基本原理,从网上找资料的时候,竟然发现两个有很大差别的算法描述,而且都叫Hilditch算法.不知道那一个才是正宗的,两个算法实现的效果接近,第一种算 ...
- OpenCV学习(17) 细化算法(5)
本章我们看下Pavlidis细化算法,参考资料http://www.imageprocessingplace.com/downloads_V3/root_downloads/tutorials/con ...
- OpenCV学习(14) 细化算法(2)
前面一篇教程中,我们实现了Zhang的快速并行细化算法,从算法原理上,我们可以知道,算法是基于像素8邻域的形状来决定是否删除当前像素.还有很多与此算法相似的细化算法,只是判断的条件不一样. ...
- OpenCV学习(13) 细化算法(1)
程序编码参考经典的细化或者骨架算法文章: T. Y. Zhang and C. Y. Suen, "A fast parallel algorithm for thinning digita ...
- OpenCV学习(19) 细化算法(7)
最后再来看一种通过形态学腐蚀和开操作得到骨架的方法.http://felix.abecassis.me/2011/09/opencv-morphological-skeleton/ 代码非常简单: v ...
- c++opencv中线条细化算法
要达到的效果就是将线条尽量细化成单像素,按照论文上的Hilditch算法试了一下,发现效果不好,于是自己尝试着写了一下细化的算法,基本原理就是从上下左右四个方向向内收缩. 1.先是根据图片中的原则确定 ...
- OpenCV学习(9) 分水岭算法(3)
本教程我学习一下opencv中分水岭算法的具体实现方式. 原始图像和Mark图像,它们的大小都是32*32,分水岭算法的结果是得到两个连通域的轮廓图. 原始图像:(原始图像必须是3通道图像) Mark ...
- OpenCV学习(21) Grabcut算法详解
grab cut算法是graph cut算法的改进.在理解grab cut算之前,应该学习一下graph cut算法的概念及实现方式. 我搜集了一些graph cut资料:http://yunpan. ...
随机推荐
- python3之Django内置模板标签和过滤器
一.模板标签 内置标签: 1.autoescape 控制当前的自动转义行为,此标记采用on或者off作为参数,并确定自动转义是否在块内有效.该块以endautoescape结束标签关闭. views: ...
- mongodb的yum源配置和安装
安装前注意: 此教程是通过yum安装的.仅限64位centos系统 安装步骤: 1.创建仓库文件: vi /etc/yum.repos.d/mongodb-org-3.4.repo 然后复制下面配置, ...
- anaconda安装tensorflow后pip安装jieba出错的问题
安装jieba出错,参考https://www.cnblogs.com/minsons/p/7872647.html TypeError: parse() got an unexpected keyw ...
- Spring AOP笔记
AOP的核心概念 AOP(Aspect-Oriented Programming)面向切面编程可以实现横切点与他们所影响的对象之间的解耦.如将公共的日志.权限.事务等业务隔离出来,但不影响原来程序的逻 ...
- Treap树理解
title: Treap树理解 comments: true date: 2016-10-06 07:57:37 categories: 算法 tags: Treap树 树 Treap树理解 简介 随 ...
- HTML5学习笔记4
10.表单元素表单元素用于获取用户的输入数据form 表示HTML表单属性: action 表示表单提交的页面 method 表示表单提交的请求方式:有POST和GET两种,默认GET(P ...
- 运用Android ROM Manager应用安装ClockworkMod Recovery的详细教程
在安装ClockworkMod Recovery恢复模式之前,建议先认识下Google Android平台的ClockworkMod Recovery恢复模式 对于Android ROM Manage ...
- 盘点Linux内核源码中使用宏定义的若干技巧(1)
http://blog.chinaunix.net/uid-23769728-id-3141515.html
- 中国LINUX内核开发大会 ppt演讲资料 与 会议视频
http://www.ckernel.org/ http://pan.baidu.com/share/home?uk=2086779999&view=share#category/type=0
- DM6446开发攻略:UBOOT-2009.03移植及nand flash烧写
有关DAVINCI U-BOOT的移植,以前写过一篇u-boot-1.3.4(2008年的),其实和这个u-boot-2009.03差别不大,只不过这个u-boot-2009.03是从TI的网站上下载 ...
