题解 P1967 【货车运输】

树链剖分+线段树

思路

貌似题解里没有树链剖分和线段树的，贡献一发。

首先明确题目要求：一辆车走某条路从x城到y城的边权最小值

我们把要求分开来看：

1. 从x城到y城：我们需要走的路径将两点联通

2. 边权最小值：我们要找这条路上的限重最小值

如果你是一个货车司机（而且题目还告诉你你的汽车走多远不要油），你肯定想多运一些货物，也就要求联通两点的权值尽可能大。

又要保证联通，又要保证权值尽可能大，没错，我们需要用到最小生成树。

（如果还不理解，你可以设想一下，有两条都可以从a到b，一条路限重10，一条路限重100，你一定会选择第二条路；我们再推广一下，如果两条路都能联通还未联通的a、b两个联通块（你可以认为a、b是两个岛，两条路是跨岛大桥），一条路限重10，一条路限重100，你还是一定会选择第二条路）

最小生成树的方法：先按边权大小排序，利用并查集判断两块是否联通，生成一个新的图

---

好，现在第一个问题解决了：你运货的最大路径方案一定在新的图（树）上了，怎么求两点之间权值最小的呢？

因为这是一棵树，所以两点之间路径唯一，可是直接搜索时间又肯定承受不住，我们这时就可以采用树链剖分了

这是类似树剖板题的题，就有提到求某两点的最值问题

值得一提的是：树剖+线段树只是支持修改和查询点权的，这时我们就需要知道怎么将边权转换为点权

边权与点权之间的转换

随便在网上找了个图：我们这样实现边权与点权之间的转换：将根节点的点权设为INF，然后所有边权下放到连接的点（所有边权往下挪到了点里，由于根节点值为INF不影响min的计算（同理，查询最大值就设为-INF））

然后直接查询就好啦！

怎么可能？！

刚开始的时候，我转换完后就直接像树剖板题那样求最值了，结果只有10分，那么问题出在哪呢？

我们看一下这个图（黑色是边权，黄色是转换后的点权）：

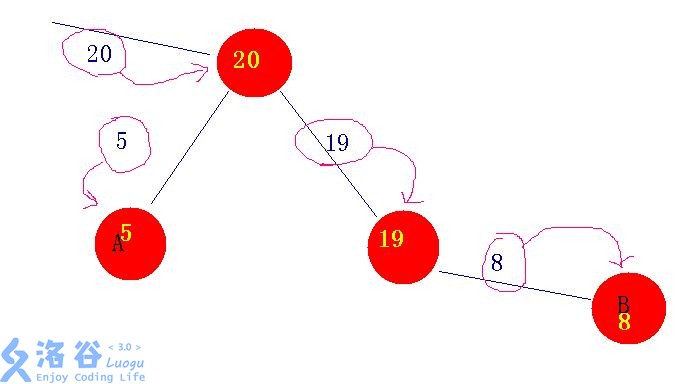
若想查询A点到B点的最值，我们会发现，按普通树剖的查询方法，我们会访问20那个点（5-20-19-8），然而应该访问的路径是5-19-8，所以我们要对查询函数做一些修改，“绕开那些点”

void getans(int x,int y){
    if(findfather(x) != findfather(y)){
        printf("-1\n");
        return ;
        }
    int ans = INF;
    while(top[x] != top[y]){
        if(dep[top[x]] < dep[top[y]])swap(x,y);
        ans = min(ans,query(1,pos[top[x]],pos[x]));
        x = fa[top[x]];
        }
    if(x == y){
        printf("%d\n",ans);//绕开
        return ;
        }
    if(dep[x] > dep[y])swap(x,y);
    ans = min(ans,query(1,pos[x] + 1,pos[y]));//+1绕开
    printf("%d\n",ans);
    }

AC代码

#include<iostream>
#include<vector>
#include<queue>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int RD(){
    int out = 0,flag = 1;char c = getchar();
    while(c < '0' || c >'9'){if(c == '-')flag = -1;c = getchar();}
    while(c >= '0' && c <= '9'){out = out * 10 + c - '0';c = getchar();}
    return flag * out;
    }
const int maxn = 500190,INF = 999999999;
int num,nr,nume,na,cnt,numt;
int head[maxn];
struct Node{
    int v,nxt,dis;
    }E[maxn * 2];
void add(int u,int v,int dis){
    E[++nume].nxt = head[u];
    E[nume].v = v;
    E[nume].dis = dis;
    head[u] = nume;
    }
struct R{
    int u,v,dis;
    }I[maxn];
bool cmp(R a,R b){
    return a.dis > b.dis;
    }
int father[maxn];
int findfather(int v){
    if(father[v] == v)return v;
    return father[v] = findfather(father[v]);
    }
void Union(int a,int b){
    int faA = findfather(a);
    int faB = findfather(b);
    if(faA != faB)father[faA] = faB;
    }
void buildG(){//建最小生成树
    for(int i = 1;i <= nr;i++){
        if(findfather(I[i].u) != findfather(I[i].v)){
            add(I[i].u,I[i].v,I[i].dis);
            add(I[i].v,I[i].u,I[i].dis);
            Union(I[i].u,I[i].v);
            }
        }
    }
int dep[maxn],fa[maxn],wson[maxn],top[maxn],size[maxn],pos[maxn],ori[maxn];
int val[maxn];
int vis[maxn];
void dfs1(int id,int F){
    vis[id] = true;
    numt++;
    size[id] = 1;
    for(int i = head[id];i;i = E[i].nxt){
        int v = E[i].v;
        if(v == F)continue;
        dep[v] = dep[id] + 1;
        fa[v] = id;
        val[v] = E[i].dis;
        dfs1(v,id);
        size[id] += size[v];
        if(size[v] > size[wson[id]]){
            wson[id] = v;
            }
        }
    }
void dfs2(int id,int TP){
    top[id] = TP;
    pos[id] = ++cnt;
    ori[cnt] = id;
    if(!wson[id])return ;
    dfs2(wson[id],TP);
    for(int i = head[id];i;i = E[i].nxt){
        int v = E[i].v;
        if(v == fa[id] || v == wson[id])continue;
        dfs2(v,v);
        }
    }
#define lid (id << 1)
#define rid (id << 1) | 1
struct sag_tree{
    int l,r;
    int min;
    int lazy;
    }tree[maxn << 2];
void build(int id,int l,int r){
    tree[id].l = l;
    tree[id].r = r;
    if(l == r){
        tree[id].min = val[ori[r]];
        return ;
        }
    int mid = l + r >> 1;
    build(lid,l,mid);
    build(rid,mid + 1,r);
    tree[id].min = min(tree[lid].min,tree[rid].min);
    }
int query(int id,int l,int r){
    if(tree[id].l == l && tree[id].r == r){
        return tree[id].min;
        }
    int mid = tree[id].l + tree[id].r >> 1;
    if(mid < l){
        return query(rid,l,r);
        }
    else if(mid >= r){
        return query(lid,l,r);
        }
    else{
        return min(query(lid,l,mid),query(rid,mid + 1,r));
        }
    }
void getans(int x,int y){
    if(findfather(x) != findfather(y)){
        printf("-1\n");
        return ;
        }
    int ans = INF;
    while(top[x] != top[y]){
        if(dep[top[x]] < dep[top[y]])swap(x,y);
        ans = min(ans,query(1,pos[top[x]],pos[x]));
        x = fa[top[x]];
        }
    if(x == y){
        printf("%d\n",ans);
        return ;
        }
    if(dep[x] > dep[y])swap(x,y);
    ans = min(ans,query(1,pos[x] + 1,pos[y]));
    printf("%d\n",ans);
    }
int main(){
    num = RD();nr = RD();
    for(int i = 1;i <= num;i++){
        father[i] = i;
        }
    for(int i = 1;i <= nr;i++){
        I[i].u = RD();
        I[i].v = RD();
        I[i].dis = RD();
        }
    sort(I + 1,I + 1 + nr,cmp);
    buildG();
    int s = 1;
    while(s <= num){
        if(vis[s] == false){
            dep[s] = 1;
            val[s] = INF;
            dfs1(s,-1);
            dfs2(s,s);
            }
        s++;
        }
    build(1,1,numt);
    na = RD();
    int u,v;
    for(int i = 1;i <= na;i++){
        u = RD();v = RD();
        getans(u,v);
        }
    return 0;
    }

最后，感谢大佬的帮助

大佬

广告