hdu 1978 How many ways 记忆化搜索 经典例题

How many ways

Time Limit: 3000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 1869    Accepted Submission(s): 1144

Problem Description

这是一个简单的生存游戏，你控制一个机器人从一个棋盘的起始点(1,1)走到棋盘的终点(n,m)。游戏的规则描述如下：
1.机器人一开始在棋盘的起始点并有起始点所标有的能量。
2.机器人只能向右或者向下走，并且每走一步消耗一单位能量。
3.机器人不能在原地停留。
4.当机器人选择了一条可行路径后，当他走到这条路径的终点时，他将只有终点所标记的能量。

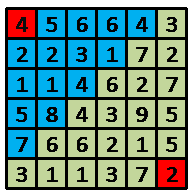
如上图，机器人一开始在(1,1)点，并拥有4单位能量，蓝色方块表示他所能到达的点，如果他在这次路径选择中选择的终点是(2,4)

点，当他到达(2,4)点时将拥有1单位的能量，并开始下一次路径选择，直到到达(6,6)点。
我们的问题是机器人有多少种方式从起点走到终点。这可能是一个很大的数，输出的结果对10000取模。

 

Input

第一行输入一个整数T,表示数据的组数。
对于每一组数据第一行输入两个整数n,m(1 <= n,m <= 100)。表示棋盘的大小。接下来输入n行,每行m个整数e(0 <= e < 20)。

 

Output

对于每一组数据输出方式总数对10000取模的结果.

 

Sample Input

1
6 6
4 5 6 6 4 3
2 2 3 1 7 2
1 1 4 6 2 7
5 8 4 3 9 5
7 6 6 2 1 5
3 1 1 3 7 2

 

Sample Output

3948

/*
记忆化搜索
*/

#include<stdio.h>
#include<stdlib.h>
#include<string.h>
int map[][];
int val[][];
int n,m;
int dfs(int x,int y)
{
    int i,j,cont,sum=;
    if(x==n && y==m) return ; //找到终点，返回。
    if(val[x][y]>) return val[x][y]; //改点值已知，返回。避免重复遍历，造成重叠。
    cont=map[x][y];
    for(i=;i<=cont;i++)
        for(j=;j<=cont;j++)
        {
            if(i+j!= && i+j<=cont &&i+x<=n && y+j<=m)
            {
                sum+=dfs(x+i,y+j);
                sum=sum%;
            }
        } //枚举所有的能到达的点.
        val[x][y]=sum;
        return sum;
}
int main()
{
    int t,i,j,k;
    while(scanf("%d",&t)>)
    {
        while(t--)
        {
            scanf("%d%d",&n,&m);
            for(i=;i<=n;i++)
                for(j=;j<=m;j++)
                    scanf("%d",&map[i][j]);
            memset(val,,sizeof(val));
            k=dfs(,);
            printf("%d\n",k);
        }
    }
    return ;
}