BZOJ 1001 题解

1001: [BeiJing2006]狼抓兔子

Time Limit: 15 Sec  Memory Limit: 162 MB
Submit: 18876  Solved: 4649
[Submit][Status][Discuss]

Description

现在小朋友们最喜欢的"喜羊羊与灰太狼",话说灰太狼抓羊不到，但抓兔子还是比较在行的，而且现在的兔子还比较笨，它们只有两个窝，现在你做为狼王，面对下面这样一个网格的地形：

左上角点为(1,1),右下角点为(N,M)(上图中N=4,M=5).有以下三种类型的道路 

1:(x,y)<==>(x+1,y) 

2:(x,y)<==>(x,y+1) 

3:(x,y)<==>(x+1,y+1) 

道路上的权值表示这条路上最多能够通过的兔子数，道路是无向的. 左上角和右下角为兔子的两个窝，开始时所有的兔子都聚集在左上角(1,1)的窝里，现在它们要跑到右下解(N,M)的窝中去，狼王开始伏击这些兔子.当然为了保险起见，如果一条道路上最多通过的兔子数为K，狼王需要安排同样数量的K只狼，才能完全封锁这条道路，你需要帮助狼王安排一个伏击方案，使得在将兔子一网打尽的前提下，参与的狼的数量要最小。因为狼还要去找喜羊羊麻烦.

Input

第一行为N,M.表示网格的大小，N,M均小于等于1000.

接下来分三部分

第一部分共N行，每行M-1个数，表示横向道路的权值. 

第二部分共N-1行，每行M个数，表示纵向道路的权值. 

第三部分共N-1行，每行M-1个数，表示斜向道路的权值. 

输入文件保证不超过10M

Output

输出一个整数，表示参与伏击的狼的最小数量.

Sample Input

3 4
5 6 4
4 3 1
7 5 3
5 6 7 8
8 7 6 5
5 5 5
6 6 6

Sample Output

14

HINT

Source

——————————————————分割线——————————————————

这道题是一道很玄学的题目，我们不能直接求它的最小割，要通过它的对偶图的最短路。那么怎么完成呢？

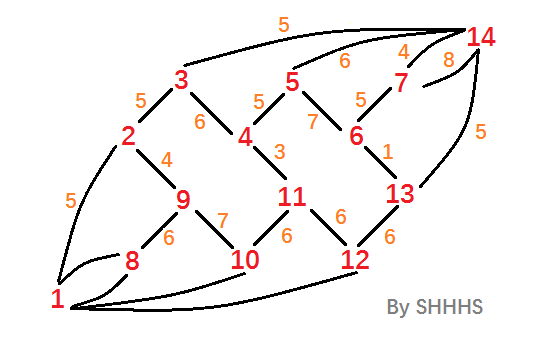
这时，只需求点1到点14的最短路就行啦。

[ATTENTION]:这道题点数总共有( N - 1 ) * ( M - 1) * 2 + 2 个，本蒟蒻被坑了好久。注意数组大小！！！

推荐一个课件：浅析最大最小定理在信息学竞赛中的应用

 /**************************************************************
     Problem: 1001
     User: shadowland
     Language: C++
     Result: Accepted
     Time:2752 ms
     Memory:165356 kb
 ****************************************************************/

 #include "bits/stdc++.h"

 using namespace std ;
 struct Edge { int to , next , val ; } ;
 const int maxN =  ;

 Edge e[ maxN ] ;
 int head[ maxN ] , Dis[ maxN ] ;
 bool vis[ maxN ] ;

 int N , M , cnt ;

 inline int INPUT ( ) {
         int x =  , f =  ; char ch = getchar ( ) ;
         while ( ch < '' || ch > '' ) { if ( ch == '-')f = - ; ch = getchar ( ) ;}
         while ( ch >= '' && ch <= '' ) { x = ( x <<  ) + ( x <<  ) + ch - '' ; ch = getchar ( ) ;}
         return x * f ;
 } 

 inline int Get ( const int x , const int y , const int z ) {
         if ( x <  || y >=M ) return ( N -  ) * ( M -  ) *  +  ;
         if ( x >= N || y <  ) return  ;
         return ( ( x -  ) * ( M -  ) + y ) * + z ;
 } 

 inline void Add_Edge ( const int x , const int y , const int _val ) {
         e[ ++cnt ].to = y ;
         e[ cnt ].val = _val ;
         e[ cnt ].next = head[ x ] ;
         head[ x ] = cnt ;
 }

 void SPFA ( const int S ) {
         memset ( vis , false , sizeof ( vis ) ) ;
         memset ( Dis , 0x3f , sizeof ( Dis ) ) ;
         queue < int > Q ;
         Dis[ S ] =  ;
         vis[ S ] = true ;
         Q.push ( S ) ;
         while ( !Q.empty ( ) ) {
                 int t = Q.front( ) ; Q.pop ( ) ; vis[ t ] = false ;
                 for ( int i=head[ t ] ; i ; i = e[ i ].next ) {
                         int temp = e[ i ].to ;
                         if ( Dis[ temp ] > Dis[ t ] + e[ i ].val ) {
                                 Dis[ temp ] = Dis[ t ] + e[ i ].val ;
                                 if ( !vis[ temp ] ) {
                                         Q.push ( temp ) ;
                                         vis[ temp ] = true ;
                                 }
                         }
                 }
         }
 }

 void DEBUG_ ( int N , int M ) {
         printf ( "\n" ) ;
         for ( int i= ; i<=(( N -  ) * ( M -  ) *  + ) ; ++i ) {
                 printf ( "%d " , Dis[ i ] ) ;
         }
 }
 int main ( ) {
         int _val ;
         scanf ( "%d %d" , &N , &M ) ;
         for ( int i= ; i<=N ; ++i ) {
                 for ( int j= ; j<M ; ++j ) {
                         _val = INPUT ( ) ;
                         Add_Edge ( Get ( i , j ,  ) , Get ( i -  , j ,  ) , _val ) ;
                         Add_Edge ( Get ( i -  , j ,  ) , Get ( i , j ,  ) , _val ) ;
                 }
         }
         for ( int i= ; i<N ; ++i ) {
                 for ( int j= ; j<=M ; ++j ) {
                         _val = INPUT ( ) ;
                         Add_Edge ( Get ( i , j -  ,  ) , Get ( i , j ,  ) , _val ) ;
                         Add_Edge ( Get ( i , j ,  ) , Get ( i , j -  ,  ) , _val ) ;
                 }
         }
         for ( int i= ; i<N ; ++i ) {
                 for ( int j= ; j<M ; ++j ) {
                         _val = INPUT ( ) ;
                         Add_Edge ( Get ( i , j ,  ) , Get ( i , j ,  ) , _val ) ;
                         Add_Edge ( Get ( i , j ,  ) , Get ( i , j ,  ) , _val ) ;
                 }
         }
         SPFA (  ) ;
         printf ( "%d\n" , Dis[ ( N -  ) * ( M -  ) *  +  ] ) ;
         //DEBUG_( N , M ) ;

         return  ;
 } 

2016-10-12 23:35:00

(完)