LOJ#2070. 「SDOI2016」平凡的骰子（计算几何）

题面

传送门

做一道题学一堆东西不管什么时候都是美好的体验呢……

前置芝士

混合积

对于三个三维向量\(a,b,c\)，定义它们的混合积为\((a\times b)\cdot c\)，其中$\times \(表示叉乘，\)\cdot\(表示点乘，记为\)[a\ b\ c]$

关于它的几何意义的话……图片来自网络

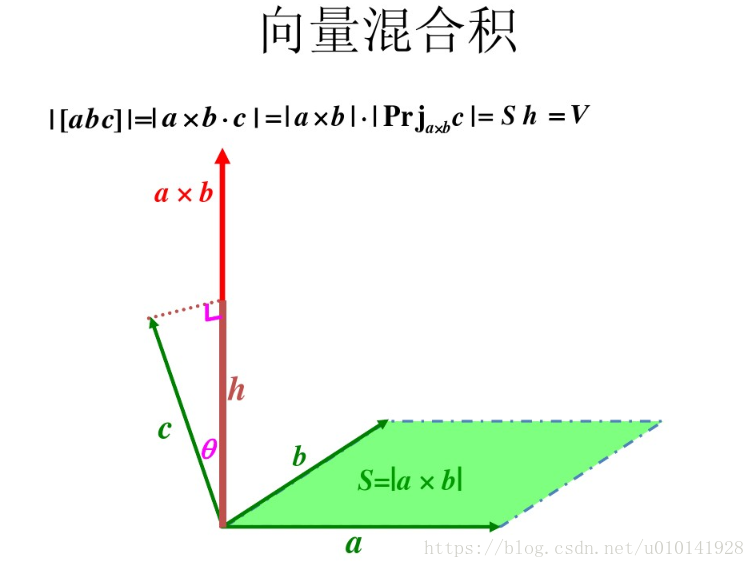
其中\(Prj_{a\times b}c\)代表的是\(c\)这个向量在\(a\times b\)这个向量上的投影

那么显然我们最后得到的是以这三个向量为三条临边的一个六面体的体积

四面体体积

假设四面体的四个顶点分别为\(A,B,C,D\)，并设三个向量\(a=B-A,b=C-A,c=D-A\)，那么这个正四面体的体积就是\({1\over 6}[a\ b\ c]\)

这个应该比较显然吧……看上面那幅图，四面体的体积是以\(ab\)这个平行四边形为底，\(c\)为顶点的棱锥的一半，而棱锥的体积是棱柱的\({1\over 3}\)，所以四面体体积就是六面体的\({1\over 6}\)了

凸多面体的重心

我们先来考虑一下凸多边形的重心好了……

对于三角形，它的重心就是它所有坐标的平均值

那么对于凸多边形，我们把它三角剖分了，记第\(i\)块的重心为\(a_i\)，面积为\(m_i\)，那么凸多边形的重心就是

\[{\sum_{i=1}^na_i\times m_i\over \sum_{i=1}^nm_i}
\]

那么凸多面体也差不多了，我们把它给四面体剖分了，然后也差不多按上面的算就好了

关于四面体剖分，具体的说我们在多面体中随便选一个点，比方说是\(p_1\)，然后把每一个面给三角剖分，那么三角形就和选定的点构成了一个四面体。设\(v_i\)表示第\(i\)个四面体的体积，\(a_i\)表示重心，则最终多面体的重心为

\[{\sum_{i=1}^na_i\times v_i\over \sum_{i=1}^nv_i}
\]

二面角

这玩意儿班里数学课正在上然而我正在停课

简单来说就是两个平面的夹角

我们假设现在有\(a,b,c\)三个向量，要求\(ab\)这个平面和\(ac\)这个平面的二面角

那么求出\(ab\)和\(ac\)的法向量（法向量可以直接用叉积算），两个法向量之间的夹角就是二面角了，法向量之间的夹角直接用点积除以长度计算

可以画个图来理解。我们俯视的话，即要求二面角\(\angle 1\)，那么显然两个法向量的夹角\(\angle 2=\angle 1\)

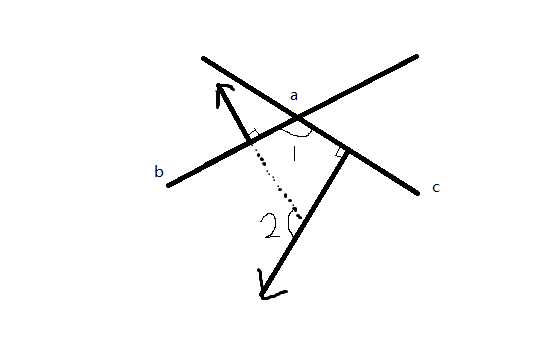
题解

总结起来的话……

三维计算几何。

需要混合积求四面体体积；

四面体剖分后合并带权重心求总重心；

四面体重心的横纵坐标是四个顶点的横纵坐标的平均数；

三维差积求平面的法向量；

点积求法向量夹角（二面角）

这些知识就可以了AC此题了。

时间复杂度\(O(nf)\)

顺便说一下数据范围是\(n,f\leq 100\)，题面里错了

//minamoto
#include<bits/stdc++.h>
#define R register
#define inline __inline__ __attribute__((always_inline))
#define fp(i,a,b) for(R int i=(a),I=(b)+1;i<I;++i)
#define fd(i,a,b) for(R int i=(a),I=(b)-1;i>I;--i)
#define go(u) for(int i=head[u],v=e[i].v;i;i=e[i].nx,v=e[i].v)
using namespace std;
const int N=105;const double Pi=acos(-1.0);
struct node{
	double x,y,z;
	inline node(){}
	inline node(R double xx,R double yy,R double zz):x(xx),y(yy),z(zz){}
	inline node operator +(const node &b)const{return node(x+b.x,y+b.y,z+b.z);}
	inline node operator -(const node &b)const{return node(x-b.x,y-b.y,z-b.z);}
	inline node operator *(const node &b)const{return node(y*b.z-z*b.y,z*b.x-x*b.z,x*b.y-y*b.x);}
	inline double operator ^(const node &b)const{return x*b.x+y*b.y+z*b.z;}
	inline node operator *(const double &b)const{return node(x*b,y*b,z*b);}
	inline node operator /(const double &b)const{return node(x/b,y/b,z/b);}
	inline double norm(){return sqrt(x*x+y*y+z*z);}
}p[N],h[N*N],u,v;
int f[N][N],c[N];double sum,tmp;
int n,m;
inline double cross(const node &a,const node &b,const node &c){
	node p=b*a,q=c*a;return acos((p^q)/p.norm()/q.norm());
}
int main(){
//	freopen("testdata.in","r",stdin);
	scanf("%d%d",&n,&m);
	fp(i,1,n)scanf("%lf%lf%lf",&p[i].x,&p[i].y,&p[i].z);
	fp(i,1,m){
		scanf("%d",&c[i]);
		fp(j,1,c[i])scanf("%d",&f[i][j]);
	}
	u=p[1],v=node(0,0,0),sum=0;
	fp(i,1,m){
		node u2=p[f[i][1]],v1,v2,t;
		fp(j,2,c[i]-1){
			v1=p[f[i][j]],v2=p[f[i][j+1]];
			t=(u+u2+v1+v2)*0.25,tmp=fabs(((v1-u2)*(v2-u2))^(u-u2));
			v=v+t*tmp,sum+=tmp;
		}
	}
	tmp=1.0/sum,u=v*tmp,tmp=0.25/Pi;
	fp(i,1,n)p[i]=p[i]-u;
	fp(i,1,m){
		sum=0;
		fp(j,2,c[i]-1)sum+=cross(p[f[i][j]],p[f[i][j-1]],p[f[i][j+1]]);
		sum+=cross(p[f[i][1]],p[f[i][c[i]]],p[f[i][2]]),
		sum+=cross(p[f[i][c[i]]],p[f[i][c[i]-1]],p[f[i][1]]);
		sum-=(c[i]-2)*Pi;
		printf("%.7lf\n",sum*tmp);
	}
	return 0;
}