BZOJ2331：[SCOI2011]地板——题解

http://www.lydsy.com/JudgeOnline/problem.php?id=2331

题面复制于洛谷

题目描述

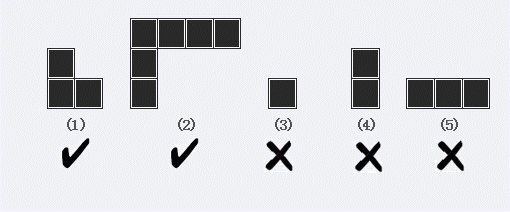
lxhgww的小名叫”小L“，这是因为他总是很喜欢L型的东西。小L家的客厅是一个R*C的矩形，现在他想用L型的地板来铺满整个客厅，客厅里有些位置有柱子，不能铺地板。现在小L想知道，用L型的地板铺满整个客厅有多少种不同的方案？需要注意的是，如下图所示，L型地板的两端长度可以任意变化，但不能长度为0。

铺设完成后，客厅里面所有没有柱子的地方都必须铺上地板，但同一个地方不能被铺多次。

输入输出格式

输入格式：

输入的第一行包含两个整数，R和C，表示客厅的大小。接着是R行，每行C个字符。'_'表示对应的位置是空的，必须铺地板；'*'表示对应的位置有柱子，不能铺地板。

输出格式：

输出一行，包含一个整数，表示铺满整个客厅的方案数。由于这个数可能很大，只需输出它除以20110520的余数。

输入输出样例

输入样例#1：

2 2
*_
__

输出样例#1：

1

输入样例#2：

3 3
___
_*_
___

输出样例#2：

8

参考了：http://blog.csdn.net/regina8023/article/details/44838887

我终于可以告别插头dp啦233333……<—此人已疯

这道题的难点在于将插头dp的插头的定义进行修改。

0：无插头

1：有插头且当前格子所在的地板能再转弯。

2：有插头且当前格子所在的地板不能再转弯。

有了这些就可以按照插头dp的思想进行分情况讨论了：

（摘自参考博客）

1.00-->22 或 10 或 01

2.11-->00

3.10-->20 或 01

20-->00 或 02

4.01-->10 或 02

02-->00 或 20

最终把所有情况枚举累加即可。

PS：第二种情况的11转换成了00实质上是11相交的地方变成了这块地板的转折点（也可以理解为两块地板并在了一起）。

#include<algorithm>
#include<cstdio>
#include<cstring>
using namespace std;
typedef long long ll;
const int INF=;
const int mod=;
const int M=;
const int p=;
struct node{
    int to,nxt;
}edge[M];
int head[M],cnt;
int n,m;
bool mp[][];
int cur,pre;
int state[][M];
ll ans[][M],cntt;
int tot[];
int bit[];
inline void getbit(){
    for(int i=;i<;i++)bit[i]=i<<;
    return;
}
inline void add(int u,int v){
    cnt++;
    edge[cnt].to=v;
    edge[cnt].nxt=head[u];
    head[u]=cnt;
    return;
}
void insert(int now,ll num){
    int u=now%mod;
    for(int i=head[u];i;i=edge[i].nxt){
        int v=edge[i].to;
        if(state[cur][v]==now){
            ans[cur][v]+=num%p;
            ans[cur][v]%=p;
            return;
        }
    }
    add(u,++tot[cur]);
    state[cur][tot[cur]]=now;
    ans[cur][tot[cur]]=num%p;
    return;
}
void plugdp(){
    cur=;
    tot[cur]=;
    ans[cur][]=;
    state[cur][]=;
    for(int i=;i<=n;i++){
        for(int j=;j<=tot[cur];j++){
            state[cur][j]<<=;
        }
        for(int j=;j<=m;j++){
            memset(head,,sizeof(head));cnt=;
            pre=cur,cur^=;
            tot[cur]=;
            for(int k=;k<=tot[pre];k++){
                int now=state[pre][k];
                ll num=ans[pre][k]%p;
                int is_down=(now>>bit[j-])%;
                int is_right=(now>>bit[j])%;
                if(!mp[i][j]){
                    if(!is_down&&!is_right)
                    insert(now,num);
                }
                else if(!is_down&&!is_right){
                    if(mp[i+][j])
                       insert(now+(<<bit[j-]),num);
                    if(mp[i][j+])
                       insert(now+(<<bit[j]),num);
                    if(mp[i][j+]&&mp[i+][j])
                    insert(now+*(<<bit[j-])+*(<<bit[j]),num);
                }
                else if(is_down&&!is_right){
                    if(is_down==){
                        if(mp[i+][j])insert(now+(<<bit[j-]),num);
                        if(mp[i][j+])insert(now-(<<bit[j-])+(<<bit[j]),num);
                    }else{
                        insert(now-*(<<bit[j-]),num);
                        if(mp[i][j+])insert(now-*(<<bit[j-])+*(<<bit[j]),num);
                    }
                }
                else if(!is_down&&is_right){
                    if(is_right==){
                        if(mp[i+][j])insert(now+(<<bit[j-])-(<<bit[j]),num);
                        if(mp[i][j+])insert(now+(<<bit[j]),num);
                    }else{
                        insert(now-*(<<bit[j]),num);
                        if(mp[i+][j])insert(now+*(<<bit[j-])-*(<<bit[j]),num);
                    }
                }
                else if(is_down==&&is_right==)
                    insert(now-(<<bit[j-])-(<<bit[j]),num);
            }
        }
    }
    for(int k=;k<=tot[cur];k++)cntt+=ans[cur][k];
    return;
}
int main(){
    getbit();
    scanf("%d%d",&n,&m);
    if(n<m){
        swap(n,m);
        for(int i=;i<=m;i++){
            for(int j=;j<=n;j++){
                char ch=getchar();
                while(ch!='*'&&ch!='_')ch=getchar();
                if(ch=='_')mp[j][i]=;
            }
        }
    }else{
        for(int i=;i<=n;i++){
            for(int j=;j<=m;j++){
                char ch=getchar();
                while(ch!='*'&&ch!='_')ch=getchar();
                if(ch=='_')mp[i][j]=;
            }
        }
    }
    plugdp();
    printf("%lld\n",cntt);
    return ;
}