http://www.lydsy.com/JudgeOnline/problem.php?id=1853

题意：

在中国，很多人都把6和8视为是幸运数字！lxhgww也这样认为，于是他定义自己的“幸运号码”是十进制表示中只包含数字6和8的那些号码，比如68，666，888都是“幸运号码”！但是这种“幸运号码”总是太少了，比如在[1,100]的区间内就只有6个（6，8，66，68，86，88），于是他又定义了一种“近似幸运号码”。lxhgww规定，凡是“幸运号码”的倍数都是“近似幸运号码”，当然，任何的“幸运号码”也都是“近似幸运号码”，比如12，16，666都是“近似幸运号码”。 现在lxhgww想知道在一段闭区间[a, b]内，“近似幸运号码”的个数。

思路：

首先要明白一点的是，在N范围内找a或b的倍数的个数为：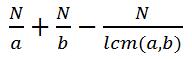

那么推广到这题的话也是差不多的，也就是容斥原理的运用。

首先可以先找出所有带6、8的数，可以优化一下删去有倍数关系的数，然后就是从中找lcm，也就是容斥原理的奇加偶减。在寻找的过程中，优先找值大的，这样一来剪枝会剪得更多一些。

 #include<iostream>

 #include<algorithm>

 #include<cstring>

 #include<cstdio>

 #include<sstream>

 #include<vector>

 #include<stack>

 #include<queue>

 #include<cmath>

 #include<map>

 #include<set>

 using namespace std;

 typedef long long ll;

 typedef pair<int,int> pll;

 const int INF = 0x3f3f3f3f;

 const int maxn = 1e5 + ;

 int n;

 ll l, r;

 ll cnt;

 ll ans;

 ll a[maxn];

 ll b[maxn];

 int vis[maxn];

 void init(ll x)

 {

     if(x>r)  return;

     if(x!=)  a[cnt++]=x;

     init(x*+);

     init(x*+);

 }

 ll gcd(ll a, ll b)

 {

     return b==?a:gcd(b,a%b);

 }

 void dfs(int cur, int cnt, ll val)

 {

     if(cur>=n)

     {

         if(!cnt)  return;

         if(cnt&)   ans+=(r/val-(l-)/val);

         else ans-=(r/val-(l-)/val);

         return;

     }

     dfs(cur+,cnt,val);

     ll tmp=val/(gcd(a[cur],val));

     if((double)tmp*a[cur]<=r)

     {

         dfs(cur+,cnt+,tmp*a[cur]);

     }

 }

 int main()

 {

     //freopen("in.txt","r",stdin);

     while(~scanf("%lld%lld",&l,&r))

     {

         cnt=;

         init();

         n=;

         sort(a,a+cnt);

         memset(vis,,sizeof(vis));

         for(int i=;i<cnt;i++)

         {

             if(!vis[i])

             {

                 b[n++]=a[i];

                 for(int j=i+;j<cnt;j++)

                 {

                     if(a[j]%a[i]==)

                         vis[j]=;

                 }

             }

         }

         for(int i=;i<n;i++)

             a[i]=b[n-i-];

         ans=;

         dfs(,,);

         printf("%lld\n",ans);

     }

     return ;

 }

BZOJ 1853: [Scoi2010]幸运数字（容斥原理）的更多相关文章

  1. Bzoj 1853: [Scoi2010]幸运数字 容斥原理,深搜

    1853: [Scoi2010]幸运数字 Time Limit: 2 Sec  Memory Limit: 64 MBSubmit: 1774  Solved: 644[Submit][Status] ...

  2. BZOJ 1853: [Scoi2010]幸运数字

    1853: [Scoi2010]幸运数字 Time Limit: 2 Sec  Memory Limit: 64 MBSubmit: 2117  Solved: 779[Submit][Status] ...

  3. bzoj 1853: [Scoi2010]幸运数字 容斥

    1853: [Scoi2010]幸运数字 Time Limit: 2 Sec  Memory Limit: 64 MBSubmit: 1170  Solved: 406[Submit][Status] ...

  4. 1853: [Scoi2010]幸运数字[容斥原理]

    1853: [Scoi2010]幸运数字 Time Limit: 2 Sec  Memory Limit: 64 MBSubmit: 2405  Solved: 887[Submit][Status] ...

  5. bzoj 1853: [Scoi2010]幸运数字&&2393: Cirno的完美算数教室【容斥原理】

    翻了一些blog,只有我用状压预处理嘛2333,.把二进制位的0当成6,1当成8就行啦.(2393是2和9 然后\( dfs \)容斥,加上一个数的\( lcm \),减去两个数的\( lcm \), ...

  6. ●BZOJ 1853 [Scoi2010]幸运数字

    题链: http://www.lydsy.com/JudgeOnline/problem.php?id=1853 题解: 容斥原理,暴力搜索,剪枝(这剪枝剪得真玄学) 首先容易发现,幸运号码不超过 2 ...

  7. 【BZOJ 1853】 1853: [Scoi2010]幸运数字 （容斥原理）

    1853: [Scoi2010]幸运数字 Time Limit: 2 Sec  Memory Limit: 64 MBSubmit: 2472  Solved: 911 Description 在中国 ...

  8. BZOJ2393 & 1853 [Scoi2010]幸运数字 【搜索 + 容斥】

    题目 在中国,很多人都把6和8视为是幸运数字!lxhgww也这样认为,于是他定义自己的"幸运号码"是十进制表示中只包含数字6和8的那些号码,比如68,666,888都是" ...

  9. BZOJ1853 [Scoi2010]幸运数字 容斥原理

    欢迎访问~原文出处——博客园-zhouzhendong 去博客园看该题解 题目传送门 - BZOJ1853 题意概括 求一个区间范围内,近似幸运数字的个数. 定义: 幸运数字:仅由6或者8组成的数字. ...

随机推荐

  1. Python老王视频习题答案

    基础篇2:一切变量都是数据对象的引用sys.getrefcount('test') 查看引用计数变量命名不能以数字开头编码:ascii.unicode.utf-81.阅读str对象的help文档,并解 ...

  2. dd命令测试硬盘IO

    1.用Linux自带的命令dd测试硬盘IO,如下------------------------------------写: [root@server102 ~]# time dd count= of ...

  3. numpy基本方法总结 --good

    https://www.cnblogs.com/xinchrome/p/5043480.html 一.数组方法 创建数组:arange()创建一维数组:array()创建一维或多维数组,其参数是类似于 ...

  4. 前端~HTML~CSS~JavaScript~JQuery~Vue

    HTML CSS JavaScript DOM文档操作 jQuery实例 Vue

  5. toml-lang - Tom's Obvious, Minimal Language

    Tom's Obvious, Minimal Languagehttps://github.com/toml-lang/toml

  6. 优云老王的心路历程（二）：下一站Web体验监控产品

    在上一篇文章中,和大家聊到了建立Web应用体验监控体系,经过了概念阶段,也完成了技术选型,就进入了把实质性的产品研发阶段.作为产品经理,时刻不敢忘记我们的产品目标:无限感知你的用户,建立完备的体验监控 ...

  7. Spark Shuffle调优原理和最佳实践

    对性能消耗的原理详解 在分布式系统中,数据分布在不同的节点上,每一个节点计算一部份数据,如果不对各个节点上独立的部份进行汇聚的话,我们计算不到最终的结果.我们需要利用分布式来发挥Spark本身并行计算 ...

  8. samba文件共享服务配置(multiuser机制)二 （共两节）

    smb客户端的multiuser挂载技术 --管理员只需要作一次挂载 --客户端在访问挂载点时,若需要不同权限,可临时切换新的共享用户[无需重新挂载] 实现方式 --挂载smb共享时启用multius ...

  9. 39XML文档类

    Xml源代码 domxml.h #ifndef DOMXML_H #define DOMXML_H #include <QString> #include <QStringList& ...

  10. ZOJ Monthly, January 2019

    A: Little Sub and Pascal's Triangle Solved. 题意: 求杨辉三角第n行奇数个数 思路: 薛聚聚说找规律,16说Lucas 答案是 $2^p \;\;p 为 n ...