从Bayesian角度浅析Batch Normalization

前置阅读：http://blog.csdn.net/happynear/article/details/44238541——Batch Norm阅读笔记与实现

前置阅读：http://www.zhihu.com/question/38102762——知乎网友

Deep Learning与Bayesian Learning在很多情况下是相通的，随着Deep Learning理论的发展，

我们看到，Deep Learning越来越像Bayesian Learning的一个子集，Deep Learning的高手当中，

很多也是Bayesian Learning高手，尤其是Hinton一门，嘲讽Hinton只会神经玄学的可以去一边凉快了。

尤其是Hinton的首席弟子——Russ Salakhutdinov，对Bayesian Learning的造诣相当高。

Deep Learning的很多做法，从Bayesian角度都可以合理给出解释。

相反，Vapnik的统计机器学习，看起来就和Bayesian背道而驰。

ICML 2015火起来的Batch Normalization，同样也有一些Bayesian的道理。

零均值、单位方差

L2-NORM

零均值、等量方差的高斯分布在贝叶斯拟合领域有个重要身份——L2-NORM

在PRML的序章，Bishop揭示了L2-NORM的由来：

I、似然函数*先验分布=后验分布

II、log(后验分布)=log(似然函数)+L2-NORM

很不巧的是，这个先验分布恰恰是零均值、等量方差的高斯分布：

$N(w|0,\alpha^{-1}I)$

不过较为特殊的是，等量方差仅限于协方差矩阵的对角线，这与Batch Norm的简化方差是相同的处理。

Regularizer

PRML读书后记(一): 拟合学习解释了加入等量方差之后，后验分布的拟合会受到一种压制之力。

在式 $-ln\,p(w|T)= \frac{\beta}{2}\sum _{n=1}^{N}\{t_{n}-w^{T}\phi (x_{n})\}^{2}+\frac{\alpha}{2}W^{T}W+const$  中，

如果我们考虑将等量方差设为1，即$\alpha=1$，那么在L2-NORM中，对参数$W$的压制是相当大的。

这点在从参数$W$，迁移到输入$X$的时候，效果仍然存在。

固定输入$X$的高斯分布，本质是压制输入$X$的波动，进而均衡各层的输入量级。

共轭分布与表征破坏

与在目标函数里加入先验分布的假设一样，对输入做标准化，依然会改变其分布。

做标准化的分布，会以共轭分布的形式，叠加至原始分布中。

考虑这么一种情况：

假设在神经网络某层激活之后，传递的新一层当中，我们得到关于输出的分布$P(X)$，

如果我们在学习一群猫，那么$P(X)$就可能是关于描述一张猫脸的概率分布。

这种理解，来自于对Deep Learning与Bayesian Learning的结合，即:

神经网络的逐层抽象，本身就是对自然物体在自然界中存在的概率建模。

单独从传统Bayesian Learning角度看，我们很少会考虑对图像的特征概率建模，

如何计算一张图的概率？

CV界的老一辈大牛会告诉你，根本不可能，乖乖用人工特征吧。

但是神经网络却可以做到这点，基于误差的修正，本身是可以近似出图像的特征概率的。

这种想法，在早期，对于传统CV界，以及传统Bayesian界，都是天方夜谭，但是Deep Learning却做到了。

Salakhutdinov教授在2015年的BPL中，更进一步，对图像特征的概率建模，大胆，而且有趣。

而且也证明了一点，对图像特征的直接概率建模比基于误差迭代计算概率的Deep Learning更有效率，

前者只需要使用很少的数据，后者则需要要庞大的数据支持，才能得到图像的概率建模。

单独从传统Deep Learning来看，这个是老问题了，很多人认为Deep Learning就是玄学，

其实是他们没有将其与Bayesian贯通起来，熟悉Bayesian的人，不会觉得Deep Learning是毫无理论的玄学，

Hinton的RBM就是Bayesian与神经网络结合的最好例子。

回到主题，对一张猫脸的分布$P(X)$，进行normalize，

相当于得到一个后验分布：

$P(MAP)=P(X)P(NORM)$

这个后验分布是一个双刃剑：

I、一方面，它有利于训练收敛。

II、另一方面，你觉得这张猫脸会不会被扭曲？会不会少了耳朵？缺了鼻子或是眼睛？

第二点你不用猜了，对原始表征分布的破坏是必然的，这会造成模型容量的下降。

猫脸的耳朵不见了，鼻子不见了，眼睛不见了，就需要额外的W去拟合。

假设W的数量是一定的，额外的W会被其他表征竞争，就可以造成模型容量下降了。

这点可以从L2-NORM角度理解，破坏了$P(X)$之后，必然会波及到$P(W)$。

L2-NORM降低模型容量也是一个事实了。

在这点上，作者在论文里给出一个误导解释，那就是举了一个不恰当的例子：

normalize，在sigmoid当中，只会利用线性部分，在论文配图中，确实给出了证明。

这个例子本身是对的，但是用来解释表征破坏就是牵强的，

甚至在happynear的文章中就理解错了，认为逆转回去的参数$\beta$、$\gamma$，是在校正激活函数的激活范围。

实际上并不是，将normalize的$\hat{X}$逆转回去，是为了在加速收敛和表征破坏之间，留一个trade off的空间。

表征缠绕

表征之间存在着复杂的缠绕关系，这在Deep Learning和Sparse Coding中已经成为共识。

normalize之后，将对这些缠绕关系造成破坏。

用逆思维考虑，如果能够直接暴力拆掉这些缠绕，比如PCA或者ZCA，

那还要RBM或者AutoEncoder干嘛？还要Deep Learning干嘛？

在Bengio的[Learning Deep Architectures for AI]中，AutoEncoder/RBM被解释成了智能化的PCA

因为它能智能化地拆解数据的非线性缠绕关系，当然是得益于BP算法的对比误差校正。

你觉得normalize像是一个智能拆解的工具嘛？显然不是。

所以，Batch Normalization最大的亮点在于，模仿AutoEncoder/RBM，添加逆转参数，

让梯度流经过，做二次tuning，对为了追求加速收敛而造成的破坏表征，进行一次修复工作。

当然，这个修复是不可能100%完成的，正如AutoEncoder/RBM不可能由$\hat{X}$复现出$X$一样。

Covariate Shift VS Internal Covariate Shift

关于Covariate Shift，知乎已经给出了不错的解释。

但是针对Internal Covariate Shift，我们又被作者误导了。

Covariate Shift ≠ Internal Covariate Shift，前者是迁移学习问题，后者是一个训练优化问题。

正如知乎的层主所说的那样，各层添加零均值、单位方差的共轭分布，只针对数值，而不针对表征。

实际上，如果把表征也”共荣化“，那就反而糟糕了。

多层神经网络可以看作是一个迁移学习问题，层与层之间的抽象等级不同，

比如学习一只猫，经过多层神经网络抽象后，就可以迁移分裂成多个机器学习问题：

学习猫脸、学习猫腿、学习猫身、学习猫爪、学习猫尾。

如果normalize之后，这五个部分的表征分布都变一样了，那么Deep Learning不是可以废掉了？

所以说，normalize仅仅是数值层面的均衡化，以及表征层面的轻度破坏化。

Internal Covariate Shift只针对数值偏移，而Covariate Shift才针对表征偏移。

BN as a Regularizer

来自[Segedy15]，也就是著名的Inception V3的观点，见第四节末：

This also gives a weak supporting evidence for the conjecture that batch normalization acts as a regularizer.

再从贝叶斯观点来看，BN其实没啥稀奇的，就是共轭一个高斯分布而已，自然同L2一样。

个人比较支持Segedy大神认为BN也是一个regularizer。

均衡的数值体系

Gradient Vanish

Gradient Vanish问题是深度神经网络优化的头号难题。(Bengio组证明了局部最小值有有益的)

从目前来看，造成Vanish的有两种原因，论文提了一处，就是Sigmoid函数问题。

当$X$变大时，$Sigmoid\,'(X)\rightarrow 0$ 。

考虑一下，何时$X$变大？网络从后往前时，这样，Sigmoid深度网络的梯度衰减了相当严重。

那是不是换成了ReLU，就没有Gradient Vanish了？显然你太天真了。

Hinton在2015年的剑桥讲座中，给了一张有趣的图，见 神经网络模型算法与生物神经网络的最新联系：

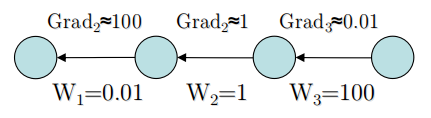
这是使用了ReLU的梯度流动图，我们可以看到，替换Sigmoid为ReLU之后，

较低层的梯度已经得到了很好的缩放了。

让我们仔细推敲一下梯度计算公式：

设$y=Wx$，则$\frac{\partial y}{\partial W}=x$

看起来没有什么问题。

当迁移到深度神经网络当中，我们又有：

$\frac{\partial l}{\partial y_{1}}\frac{\partial y_{1} }{\partial y_{2}}\frac{\partial y_{2} }{\partial y_{3}}.....\frac{\partial y_{n} }{\partial y}\frac{\partial y }{\partial W}$

化简一下：

$\frac{\partial l}{\partial y_{1}}W_{1}W_{2}W_{3}.......W_{n}\frac{\partial y }{\partial W}$

中间冗长的W累积，是Gradient Vanish的真正原因，在RNN中，Gradient也有同样的问题。

以LSTM的观点来看，这大概可以视作是BP链路承载了太多冗余信息，衰减是必然的。

但LSTM使用了门控电路的方法，由神经网络嵌套神经网络，对梯度链路进行了智能裁剪，

以达到跳跃中间某些信息，到达反向传播底层的目的，详情见 Long-Short Memory Network(LSTM长短期记忆网络)

再次回到这张图：

可以看到，从W3到W1，W衰减的相当厉害，累积之后依然可以造成可观的Vanish。

这种逐层衰减有一个直接诱因，就是输入$X$波动比较厉害。

直观上来说，对于一个网络层：

I、$X$大点，$W$肯定要小点。

II、$X$小点，$W$肯定要大点。

违反这两条，会让激活值处于函数边界，从而被自然选择淘汰掉（有点遗传算法的味道）。

另一方面，从初始化方案来看，我们也能看到，对$W$的初始化范围是逐层递增的。

这是经典的大拇指规则(Rule of Thumb)，由无数前辈的实验得到，似乎已经成了共识。

normalize之后，各层的$X$遭到了压制，并且向高斯分布中心进行数值收缩。

进而，由$X$影响到了$W$，$W$也向高斯分布中心进行数值收缩。

这样，$W_{1}W_{2}W_{3}.......W_{n}$的衰减将会得到可观的减缓。

这大概是Batch Normalization可以减轻使用ReLU的Gradient Vanish的直接原因。

Sigmoid

如果上一部分的推测是对的，那么可以使用Sigmoid的原因，就独立开来了。

正如论文中的那张配图：

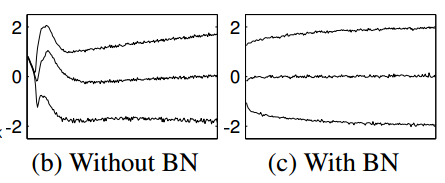
可以看到，Sigmoid函数的输入值$X$几乎是被压制到了线性响应部分。

这时候，两端的侧抑制似乎是没有多少用的，Sigmoid已经开始向ReLU近似。

此时，$Sigmoid\,'(X)$为趋于0的可能性已经不大了。

Over Fitting

正如第一章从Beyesian角度分析一样，收缩了$P(X)$之后，也波及到$P(W)$。

$W$数值的整体量级得到了削减。

PRML读书后记(一): 拟合学习、关于过拟合、局部最小值、以及Poor Generalization的思考中，

给出了维数灾难形象描述。

$W$的数值收缩，从维数灾难角度理解，撇开降维这种暴力方法，一定程度上可以减轻过拟合问题。

Learning Rate

论文中应该给出的是稍大，而不是无限大。

事实上，你要是给个比较大的学习率，还是会导致目标函数发散。

包括在训练后期，你要不把学习率降低量级，训练有很大可能从函数谷面跑飞过去了。(亲测)

个人推测，应该是$X$、$W$、$Gradient$被均衡后，量级得到收缩，允许稍大的学习率存在。

二阶近似优化方案，ADADELTA以及RMSPROP，免除人工干扰学习率的困扰。

ADADELTA详细参考：自适应学习率调整：AdaDelta

Dropout

从我实际测试来看，非常不鼓励扔掉Dropout。

Batch Norm根本压不住大模型在训练后期的过拟合。

我甚至还是保留着50%的Dropout，速度也还不错。

Dropout的两个作用：稀疏与动态平均，不仅从数值上抑制过拟合。

在表征训练方面，也有一定的regularize效果。

编程技巧

BN有两种写法，合并式和分离式。

Caffe master branch采用的是分离式写法，CONV层扔掉bias，接一个BN层，再接一个带bias的SCALE层。

我个人更推崇合并式写法，这样在深度网络定义文件中，可以不用眼花缭乱。

从执行速度来看，合并式写法需要多算一步bias；

分离式写法，在切换层传播时，OS需要执行多个函数，在底层（比如栈）调度上会浪费一点时间。

可以说，各有优劣。默认推荐https://github.com/ducha-aiki/caffe的合并式写法。

分离式写法，见官方master branch。

代码

默认实现在我的Dragon框架下，只提供GPU代码，Caffe稍作修改即可，CPU也稍作修改即可。

(注意dragon_copy和caffe的是相反的)

https://github.com/neopenx/Dragon/blob/master/Dragon/layer_include/common_layers.hpp

https://github.com/neopenx/Dragon/blob/master/Dragon/layer_src/batch_norm_layer.cpp

(forward、backward是错的，参考cu文件里的写法)

https://github.com/neopenx/Dragon/blob/master/Dragon/layer_src/batch_norm.cu

还有proto：

message BatchNormParameter{
    optional bool use_global_stats= [default=true];
    optional float decay= [default=0.95];
    optional float eps= [default=1e-];
}

message LayerParameter{
    .......
    optional BatchNormParameter batch_norm_param=xxx;
    .......
}

精度eps推荐1e-10，1e-5在cifar10中已经过大了。

$\beta$、$\gamma$的初始化

论文里没说，https://github.com/ducha-aiki/caffe/blob/elu/examples/BN-nator.ipynb中给出的方案是：

$\beta$为常数0.0000001，$\gamma$为常数1.0000001

我测了几次，发现用0和1的效果好像随机出来不是很好，推测是精度问题？还是我人品太差了？

全局统计测试

论文默认推荐是开启全局统计测试，也就是记录每次batch的均值和方差。

在测试的时候，用累积和的期望值。无偏估计的系数可以忽略，意义不大。

我与ducha-aiki的方案不同之处，在于用blob[4]记录总batch数量，

在训练的时候，利用：

(均值*数量+新值)/(数量+1)来更新

在测试的时候，直接copy过来，然后做norm。

在cifar10测试中，我发现，对于batch为100的验证集，精度会比不做全局统计差很多。

可能是，训练次数过低，导致的全局统计值不是很稳定。

在追加了一定训练次数之后，在cifar10 quick epoch12时，

差距仍然达到了8%，(66% vs 74%)。

所以不推荐在测试数据充裕的情况下，做全局统计测试，往往会得到不好的结果。(写论文注意)

相反，对于实际使用的时候，测试数据就几个，这时候做一做效果还是可以的。

不过还是看人品，没准就偏移大了，不准了，这大概是Batch Norm唯一不好的地方吧。

—————————————————————————————————————————————————

在epoch达到60后，这种方法的测试精度已经退化到40%了。

仔细想了一下，发现做纯平均是错的，因为前后更新的重要度不一样。

一般我们认为，最新更新的比较重要。

所以改用ducha-aiki的moving average decay的方案。

设置decay=0.95，

每次更新的时候，最新量0.95+0.05*history，这种平均比纯平均期望意义更大。

后者在训练末期，数值体系已经被纯平均搞得崩溃了。

使用这种滑动平均期望后，默认的验证和测试，开启全局统计就没问题了。

随机抖动

使用Batch Norm之后，每次跑程序的时候，在初期，训练似然和验证精度都有很大的变化。

有时候特别好，有时候特别差，相当不稳定。

推测应该是normalize之后，放大了随机初始化的差异问题，这个在写代码debug的时候需要注意。

多测几次，不要误判为bug。

适用范围

在https://github.com/ducha-aiki/caffe/blob/elu/examples/BN-nator.ipynb中，

我们可以看到，所有CONV和INNER_PRODUCT层都是可以做Batch Norm的。

实际测试的时候，因为波动、以及层数少的问题，没发现什么异常。

用法如下（不要像激活函数那样用成in-place)：

layer{
    name:"bn1"
    type:"BatchNorm"
    bottom:"conv1"
    top:"bn1"
}

—————————————————————————————————————————————————

由于INNER_PRODUCT层后一般习惯接DROPOUT，而且INNER_PRODUCT一般处于反向链式

前端，所以INNER_PRODUCT上的Batch Norm可能显得多余，我用浅层模型没有测出来较大的差异。

计算代价

注意论文中的：

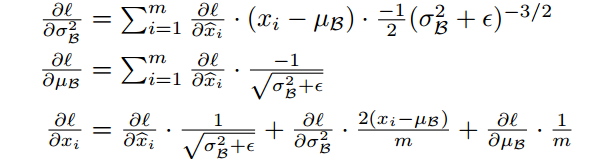
在实现的时候，是可以优化的，主要是提取公因子，x_norm.diff、-1/m，以及sqrt(..)项都可以提出来。

具体需要仔细琢磨，x_norm.diff计算出来之后，下面那几段收缩、扩展的代码，相当经典。

尽管如此，Batch Norm的计算代价还是相当大的，我觉得比卷积层还大。

所以CPU党可以不用尝试了，逐层Batch Norm实在是太慢了。