扩展KMP (ex_KMP)

一些约定：

• 字符串下标从1开始
• s[1,i]表示S的第一个到第i个字符组成的字符串

解决的题型：

给你两个字符串A,B（A.size()=n,B.size()=m）,求p数组

p[i]表示最大的len使得A[i,i+len-1]=B[1,len]

即A的第i位与B前缀的最大匹配的长度

比如;

A:aaaabaa

B:aaaa

p数组就是{4 3 2 1 0 2 1}

算法实现

1. 我们要先求一个关于B的z数组,一些定义：

• z[i]表示最大的len使得B[1,len]=B[i,i+len-1]，比如对于B:aabcaabd z[5]=3, 一开始z[1]=m

• Z-box:表示一段区间,用两个变量l,r表示，它表示目前为止B中右端点最大的一个区间[l,r]满足，B[l,r]=B[1,r-l+1] (即这段区间与它等长度的前缀相同)，一开始l=r=0,在循环求解z数组的过程中不断更新

知道了一些定义我们就来看z数组怎么求

假设我们已经得出z[1]~z[i-1]了要求z[i]，且目前的Z-box=[l,r]

（1） \(l \le i \le r\) 如下图

(实际上如果\(i \le r\) , i一定满足\(l \le i \le r\) ,因为我们是用1~i-1去更新l的)

r’表示r-l+1,则B[1,r’]=B[l,r] (为了下面叙述方便，我们称r’为r的对应点) 相同颜色代表这段区间相同

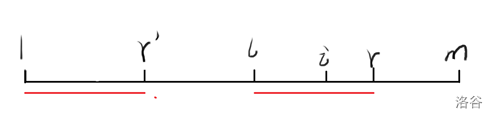
我们再求出i的对应点i’=i-l+1,则B[i’,r’]=B[i,r]

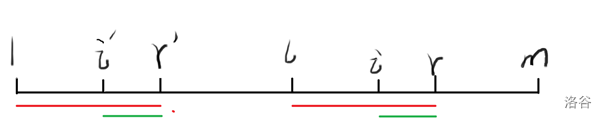
假设z[i’]=len 则B[1,len]=B[i’,i’+len-1],现在有两种情况

• \(len \le r-i+1\)：此时\(B[1,len]=B[i’,i’+len-1]=B[i,i+len-1]\)
  
  则z[i]=len

  

• 而如果 \(len>r-i+1\),如下图

  

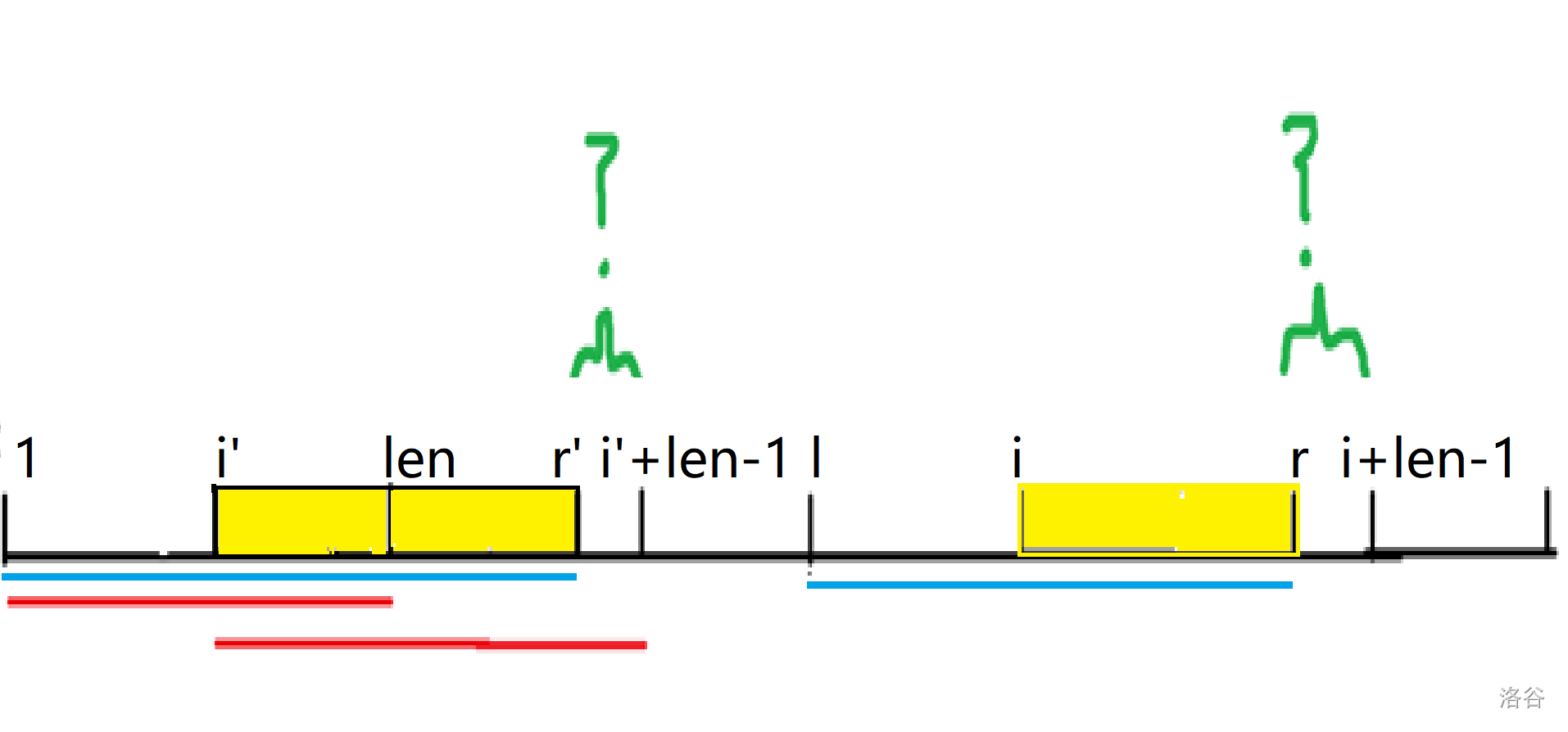
我们无法确定绿色部分是否相同，因此不能直接把len赋给z[i],但我们可以保证z[i]>=r-i+1,r后面的部分暴力扫描即可

(2)\(i>r\) 同样也是暴力往后扫描即可

注意：每次求完z[i]后如果i+z[i]-1>r 则用i和i+z[i]-1更新l,r

求z数组的代码如下

	z[1]=m,l=0,r=0;
	for(int i=2;i<=m;i++)
	{
		if(i<=r) z[i]=min(z[i-l+1],r-i+1);
		while(b[i+z[i]]==b[1+z[i]]) z[i]++; //如果i>r那这里z[i]一开始是0
		if(i+z[i]-1>r) r=i+z[i]-1,l=i;
	}

2.求解p数组过程差不多

这里的[l,r]表示最大的一段区间满足a[l,r]=b[1,r-l+1]

一开始，l=0,r=0

外层循环i从1到n (这里p[1]不用赋初值)

(1) \(l \le i \le r\) , 令i’=i-l+1,r’=r-l+1,len=z[i']:

• ① \(len \le r-i+1\),则B[1,len]=B[i’,i’+len-1]=A[i,i+len-1],所以p[i]=len

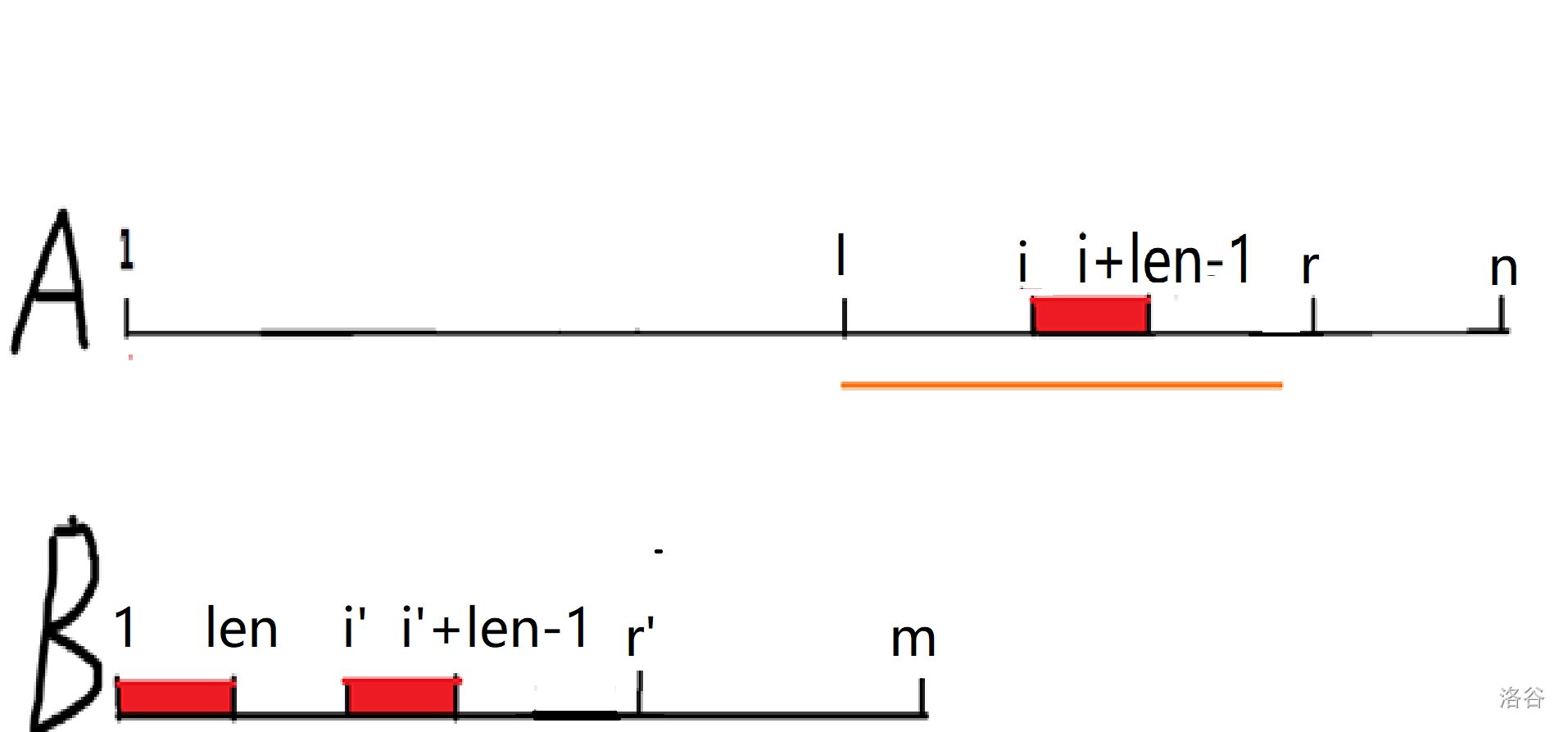
• \(len>r-i+1\),超出部分暴力扫描

(2) \(i>r\),暴力扫描

记得更新l,r

求解p数组代码

	l=0,r=0;
	for(int i=1;i<=n;i++)
	{
		if(i<=r) p[i]=min(z[i-l+1],r-i+1);
		while(a[i+p[i]]==b[1+p[i]]&&i+p[i]<=n&&1+p[i]<=m) p[i]++;
			//注意这里要判断边界
		if(i+p[i]-1>r) r=i+p[i]-1,l=i;
	}

最后放上一道板题

P5410 【模板】扩展 KMP/exKMP（Z 函数）

Code:

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=2e7+5;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
char a[N],b[N];
int n,m;
string s1,s2;
int z[N],p[N];
int l,r;
int ans1,ans2;
signed main()
{
	cin>>s1>>s2;
	n=s1.size(),m=s2.size();
	for(int i=1;i<=n;i++) a[i]=s1[i-1];
	for(int i=1;i<=m;i++) b[i]=s2[i-1];
	z[1]=m,l=0,r=0;
	for(int i=2;i<=m;i++){
		if(i<=r) z[i]=min(z[i-l+1],r-i+1);
		while(b[i+z[i]]==b[1+z[i]]) z[i]++;
		if(i+z[i]-1>r) r=i+z[i]-1,l=i;
	}
	for(int i=1;i<=m;i++){
		ans1^=(z[i]+1)*i;
	}
	l=0,r=0;
	for(int i=1;i<=n;i++){
		if(i<=r) p[i]=min(z[i-l+1],r-i+1);
		while(a[i+p[i]]==b[1+p[i]]&&i+p[i]<=n&&1+p[i]<=m) p[i]++;
			//注意这里要判断边界
		if(i+p[i]-1>r) r=i+p[i]-1,l=i;
	}
	for(int i=1;i<=n;i++){
		ans2^=(p[i]+1)*i;
	}
	printf("%lld\n%lld\n",ans1,ans2);
	return 0;
}

本博客参考的网址：

[C++]洛谷：【模板】扩展 KMP（Z 函数） 算法详解