机器学习-线性分类-支持向量机SVM-合页损失-SVM输出概率值-16
1. SVM概率化输出
标准的SVM进行预测 输出的结果是:

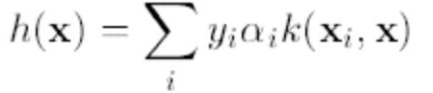
是无法输出0-1之间的 正样本 发生的概率值
sigmoid-fitting 方法:
将标准 SVM 的输出结果进行后处理,转换成后验概率
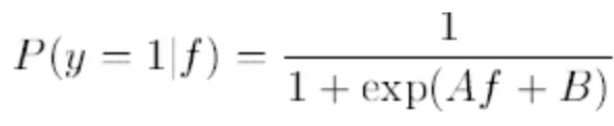
A,B 为待拟合的参数, f 为样本 x 的无阈值输出。
定义训练集为(fi,ti)

yi 为样本的所属类别,取值{-1,1}
利用之前的逻辑回归:
极小化训练集上的负对数似然函数
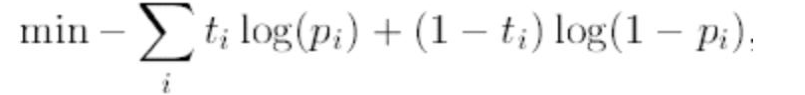
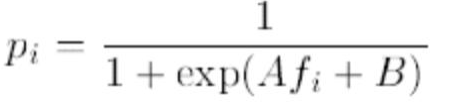
求出A和B,即可得到SVM的概率输出
import numpy as np
from sklearn.svm import SVC
X = np.array([[-1, -1], [-2, -1], [1, 1], [2, 1]])
y = np.array([1, 1, 2, 2])
cld = SVC(probability=True)
cld.fit(X, y)
print(cld.predict([[-0.8, -1]]))
print(cld.predict_proba([[-0.8, -1]]))
2. 合页损失
SVM某一条样本的损失

y(wx+b) >=1 分类正确 都没有损失
0<y(wx+b)<1 边界与超平面之间 有损失但是较小
y(wx+b)<0 彻底的分错了 loss=1+嵌入的深度
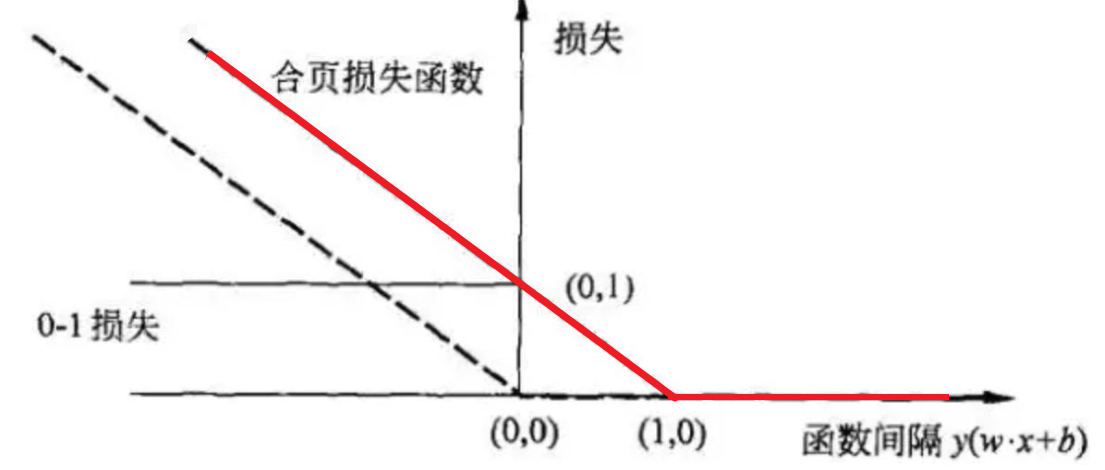
损失+正则项 得到目标函数:
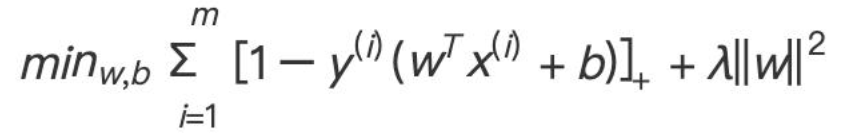
机器学习-线性分类-支持向量机SVM-合页损失-SVM输出概率值-16的更多相关文章
- 吴裕雄 python 机器学习——支持向量机线性分类LinearSVC模型
import numpy as np import matplotlib.pyplot as plt from sklearn import datasets, linear_model,svm fr ...
- 线性可分支持向量机与软间隔最大化--SVM(2)
线性可分支持向量机与软间隔最大化--SVM 给定线性可分的数据集 假设输入空间(特征向量)为,输出空间为. 输入 表示实例的特征向量,对应于输入空间的点: 输出 表示示例的类别. 我们说可以通过间隔最 ...
- 线性可分支持向量机--SVM(1)
线性可分支持向量机--SVM (1) 给定线性可分的数据集 假设输入空间(特征向量)为,输出空间为. 输入 表示实例的特征向量,对应于输入空间的点: 输出 表示示例的类别. 线性可分支持向量机的定义: ...
- svm 之 线性可分支持向量机
定义:给定线性可分训练数据集,通过间隔最大化或等价的求解凸二次规划问题学习获得分离超平面和分类决策函数,称为线性可分支持向量机. 目录: • 函数间隔 • 几何间隔 • 间隔最大化 • 对偶算法 1. ...
- 统计学习:线性可分支持向量机(SVM)
模型 超平面 我们称下面形式的集合为超平面 \[\begin{aligned} \{ \bm{x} | \bm{a}^{T} \bm{x} - b = 0 \} \end{aligned} \tag{ ...
- 简介支持向量机热门(认识SVM三位置)
支持向量机通俗导论(理解SVM的三层境地) 作者:July .致谢:pluskid.白石.JerryLead.出处:结构之法算法之道blog. 前言 动笔写这个支持向量机(support vector ...
- 支持向量机通俗导论(SVM学习)
1.了解SVM 支持向量机,因其英文名为support vector machine,故一般简称SVM,通俗来讲,它是一种二类分类模型,其基本模型定义为特征空间上的间隔最大的线性分类器,其学习策略便是 ...
- 支持向量机通俗导论 ——理解SVM的三层境界 总结
1.什么是支持向量机(SVM) 所谓支持向量机,顾名思义,分为两部分了解:一,什么是支持向量(简单来说,就是支持或支撑平面上把两类类别划分开来的超平面的向量点):二,这里的“机(machine,机器) ...
- Python实现鸢尾花数据集分类问题——基于skearn的SVM
Python实现鸢尾花数据集分类问题——基于skearn的SVM 代码如下: # !/usr/bin/env python # encoding: utf-8 __author__ = 'Xiaoli ...
- 机器学习理论基础学习3.3--- Linear classification 线性分类之logistic regression(基于经验风险最小化)
一.逻辑回归是什么? 1.逻辑回归 逻辑回归假设数据服从伯努利分布,通过极大化似然函数的方法,运用梯度下降来求解参数,来达到将数据二分类的目的. logistic回归也称为逻辑回归,与线性回归这样输出 ...
随机推荐
- free内存参数介绍
第一部分Mem行: total 内存总数: 15.7G used 已经使用的内存数: 15.6G free 空闲的内存数: 93M shared 当前已经废弃不用,总是0 buffers Buffer ...
- 玩转 K8s 权限控制:RBAC + kubeconfig 搞定 kubectl 权限管理那些事
1. 先抛需求 当一个 K8s 集群需要被多个租户共享时,就涉及到了权限问题,比如你是管理员,这时候你会面临着"给每个用户分配一个 Namespace"类似的需求. 更进一步,可能 ...
- Feign远程调用超时问题
1.问题概述 上图的场景,每次重启项目后openFeign都会报一个超时异常,异常信息如下 2.为什么会产生这个异常? 当项目刚启动时,数据库连接池的中的连接并不会创建;第一次请求的时候才会初始化各种 ...
- 生产升级JDK 17 必读手册
原文点这里,查看更多优质文章 DK 17 在 2021 年 9 月 14 号正式发布了!根据发布的规划,这次发布的 JDK 17 是一个长期维护的版本(LTS). Java 17 提供了数千个性能.稳 ...
- 【笔记】Ribbon负载均衡伪随机算法
伪随机:思路 当一个下标(伪服务)连接被调用两次,第三次如果还是它,就让再随机一次 当重复随机到一台服务两次时判断第三次是否还是它 是的话 我们要进行 再次随机 也就是第三次 package top. ...
- 2023.3 Idea配置Tomcat环境
tomcat配置 下载tomcat 先到官网(按住Ctrl再左键点击直接打开官网)下载64位的tomcat,网速慢就用魔法下 创建项目.模块 打开idea(我用的是最新的idea的专业版,ui有点变化 ...
- Vue 2 和 Vue 3 中 toRefs的区别
摘要:本文将介绍 Vue 2 和 Vue 3 中 toRefs 函数的不同用法和行为,并解释其在各个版本中的作用. 正文: Vue 是一款流行的 JavaScript 框架,用于构建用户界面.在 Vu ...
- ElasticSearch-1
原文链接:https://gaoyubo.cn/blogs/52ef5bf7.html 一.Elasticsearch 架构设计 Elasticsearch 架构层: Elasticsearch 五层 ...
- 文心一言 VS 讯飞星火 VS chatgpt (44)-- 算法导论6.1 1题
一.在高度为h的堆中,元素个数最多和最少分别是多少? 文心一言: 在高度为 h 的二叉搜索树(BST)中,元素个数最多和最少的情况分别如下: 1.最多情况:当每个节点都包含两个子节点时,BST 中的元 ...
- Karmada v1.2发布:开启全文本搜索新纪元
摘要:Karmada v1.2 版本对调度器能力做了较大增强,初步提供了分布式搜索引擎支持,此外还借助聚合API提供了诸如 logs, watch等实用的命令行工具,资源解释器(Resource In ...
