【算法day4】堆结构、堆排序、比较器以及桶排

堆与堆结构（优先级队列结构）

知识点：

• 堆结构就是用数组实现的完全二叉树结构
• 完全二叉树中如果每棵子树的最大值都在顶部就是大根堆
• 完全二叉树中如果每棵子树的最小值都在顶部就是小根堆
• 堆结构的heaplnsert与heapify操作
• 堆结构的增大和减少
• 优先级队列结构，就是堆结构

一段连续的数组是可以想象成完全二叉树结构的

例如

[3,5,2,7,1,9,6]

[0,1,2,3,4,5,6]

对应到完全二叉树结构中得到

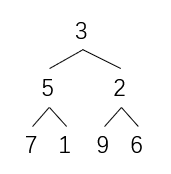
连续的一段数组可以用一个"size"描述，表示一个连续的数组到达的位置（与数组长度无关）

这个例子中的size = 7

若用数组下标表示该完全二叉树，则

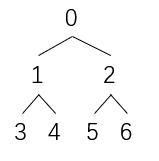
那么生成树的对应规则是：

i位置（0~6）对应的左分支为：2*i+1

例如，

0的左分支是2*0+1=1；

1的左分支是2* 1+1=1，2的左分支是2*2+1=5；

3的没有左分支，因为按照公式计算后所得超过了size,456同理

i位置（0~6）对应的右分支为：2*i+2

i位置（0~6）对应的父分支为：(i-1)/2

例如，

5位置的父分支节点是(5-1)/2=2，6位置的父分支节点是(6-1)/2=2.5，取整为2

大/小根堆

定义：在完全二叉树中，每一棵子树的最大值就是头节点的值

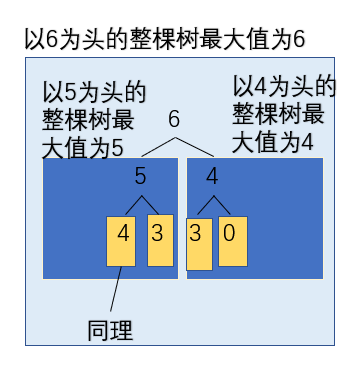
反之，则为小根堆

将连续数组表示为堆（heapinsert，将大数往上移）

假设，现在有一个数组[],设一个变量为heapsize = 0

heapsize = 0意味着数组中从0出发的连续的0个数现在构成一个堆

此时，用户给了一个数，假设是5

那么根据heapsize的指示，5被放在0位置上，heapsize+1 = 1

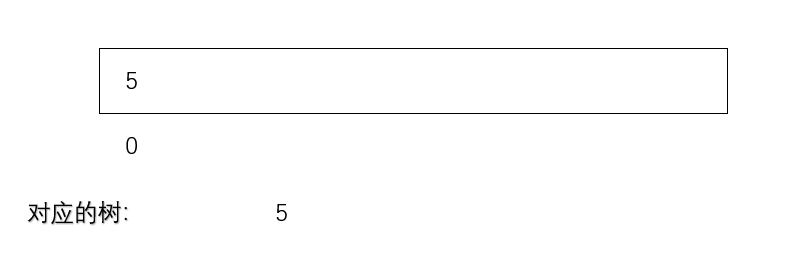
用户又给了一个数3，根据heapsize的指示，3被放在1位置上，heapsize+1 = 2

用户再给一个数6，根据heapsize的指示，6被放在2位置上，heapsize+1 = 3

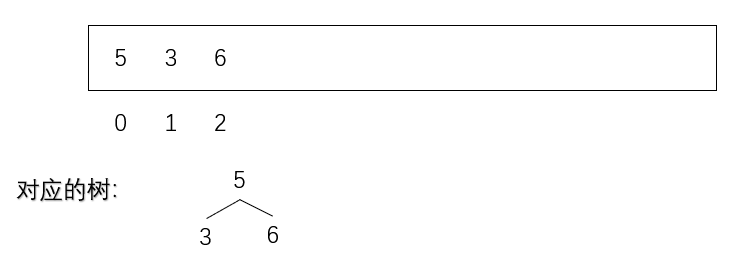
此时的树不满足“大根堆”要求，于是6就需要和自己的父去做比较

6的位置是已知的（heapsize还没变）

根据生成树的规则可以找到6的父值

父分支=(i-1)/2=(2-1)/2=0.5，取整为0

于是6需要与0位置的数（也就是5）比较大小

6比5大，于是两者交换位置，树又满足大根堆的要求了

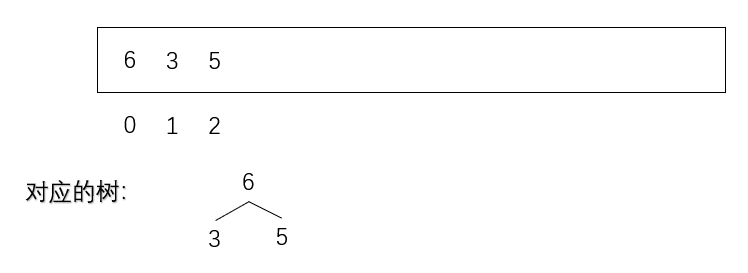
如果再进来一个更大的数也是同样的操作

规律就是，新来的数一直与自己的父值比较，若大于父值则交换，直到比较完所有的父值或者来到整棵树的头部就停止。

若小于就不动。

这样操作后可以保证用户给的每一个数到了数组里，形成的结构均为大根堆

heapify

在现有的堆中插入一个数，该数较小不符合当前位置，为了整体结构仍满足大根堆，要将其往下移，该操作称为heapify，代码实现如下

堆排序

假设有数组

[3,5,9,4,6,7,0]

[0,1,2,3,4,5,6], heapsize = 0

现在按照之前的方法从0位置到6位置让该数组排成大根堆

排完之后结果如下

数组变为由大到小的排序

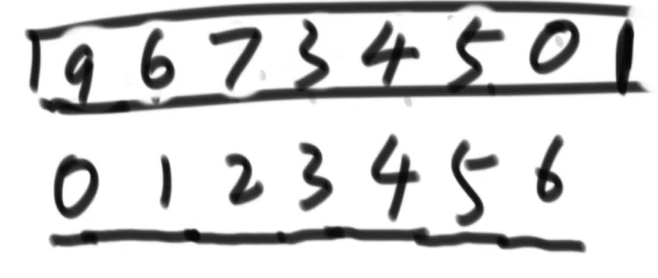
对应的树结构是，当前heapsize = 7

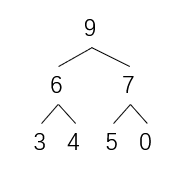
此时，将0位置的最大值与6位置的最小值交换

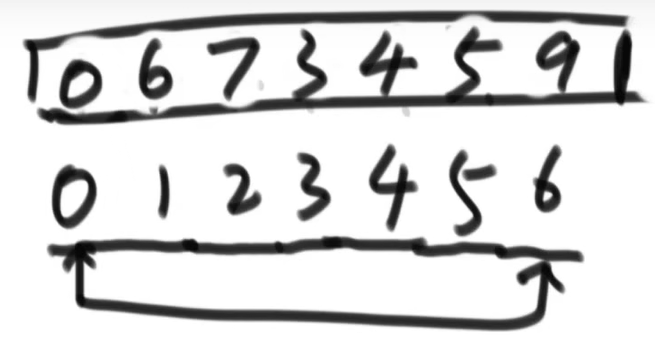
heapsize -- = 6

这样做的目的是让最大值来到堆的末尾，然后让最大值与堆断开联系（因为它是已经排好的数，堆没必要再包含它）

那么当前的树结构变为

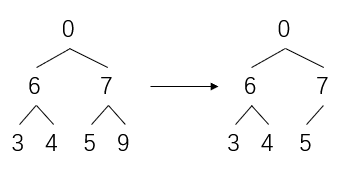
舍弃堆末尾的最大值9

然后让剩下的数继续做heapify，把0再弄到堆的末尾

排完之后结果如下

树结构

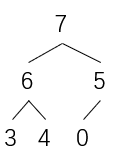
此时，又将0位置的最大值与5位置的最小值交换

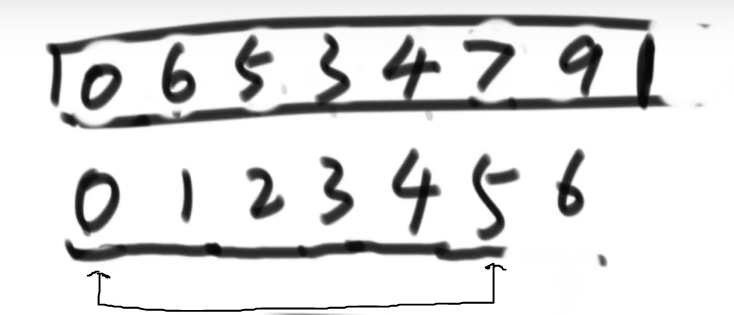
heapsize -- = 5

当前的树结构变为

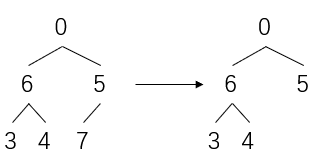
舍弃堆末尾的最大值7

然后让剩下的数继续做heapify，周而复始直到堆减为0结束

更优化的方式获取大根堆

如果我们已经知道数组中的所有数，并且只需要得到大根堆（不做别的操作）

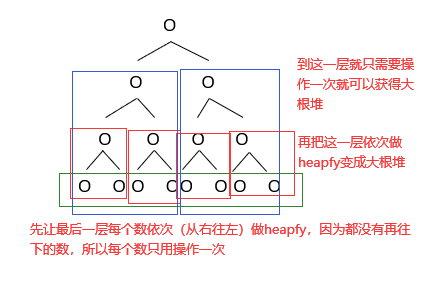
tips：

1、堆结构底层是由数组支持实现的，如果堆在不断扩大的过程中超过了数组的长度，那么数组要成倍的加长

例如，原来的数组长度是100，用完之后系统会直接给它加到200，再用完就变成400

这样，算法的空间复杂度仍然不变

2、高级语言自带的堆方法只是一个黑盒，我们可以通过add和poll与之交互，本质就是我给它一个数，它给我一个数

虽然这样在简单场景下高效，但是针对一些具体问题就不好用了

比如，我想从已经规定好的堆结构里取一个数，然后让堆仍然保持大/小根堆，自带的堆方法效率很低，只能自己手写一个

这就是为什么面试的时候经常会要求手写堆结构的原因

比较器

1）比较器的实质就是重载比较运算符

2）比较器可以很好的应用在特殊标准的排序上

3）比较器可以很好的应用在根据特殊标准排序的结构上

在C++里也叫重载运算符

简单来说，就是在比较数的时候自定义一些的规则，让比较结构变成我们想要的

例子1，

比如我调用了.sort()方法去给数组排序

排序的本质就是比较数的大小

如果上面都不加，系统可能默认从大到小排出结果

但是，我现在希望从小到大（或者指定哪些数先排等一些更复杂的排序）排，那么我就可以传一个比较器给.sort()

.sort()就可以按照比较器规定的方式进行排序（比较）

例子2，

PriorityQueue是java中的优先级队列结构（也就是系统提供的堆方法）

当不指定时，默认生成的是小根堆

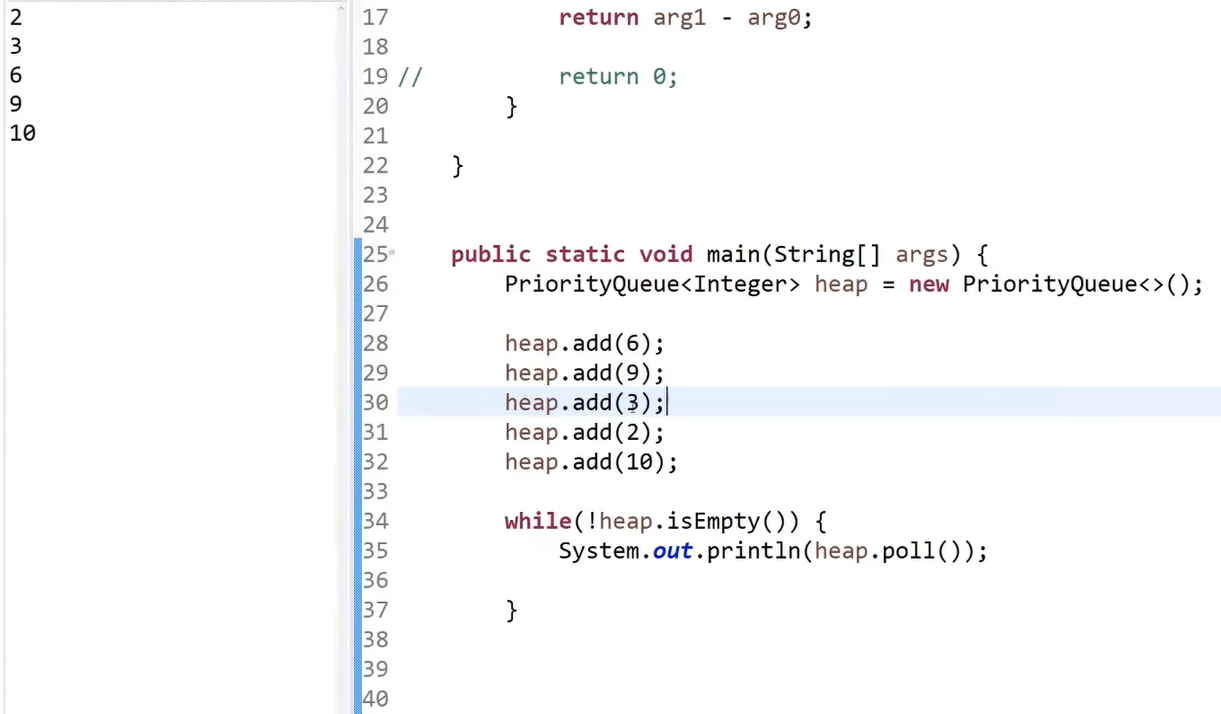
往里面添加数后poll，会按照从小到大的顺序返回值

此时，给它传一个比较器如下

这样PriorityQueue就会以大根堆的方式去构建了

比较器的应用场景

可以用于定义复杂的比较策略

例如，

我有两个数据：班级和年龄

如果想让整个数组整体按年龄来排序（小的在前），但是年龄一样的时候，班级大的排在前面

这时候可以定义比较器去实现（代码量少）

tips：

到目前为止，所有的排序算法都是基于"比较"进行的排序

也有不依靠"比较"进行的排序，但需要针对数据进行定制，往往只在特定情况下高效，使用范围较小

桶排序（基数排序）

桶排序思想下的排序

1）计数排序

2）基数排序

分析:

1)桶排序思想下的排序都是不基于比较的排序

2)时间复杂度为0(N)，额外空间负载度0(M)

3)应用范围有限，需要样本的数据状况满足桶的划分

假设有以下数

[17,13,25,100,72]

里面最大的是三位数，所以其他的数要补成三位

[017,013,025,100,072]

现在设置一些“桶”用于存放数据（桶的底层一般是队列、数组或栈，这里用的是队列）

因为是十进制的数，所以理论上最多需要十个“桶”

具体到当前问题，实际上只用了0、1、2、3、5、7这几个

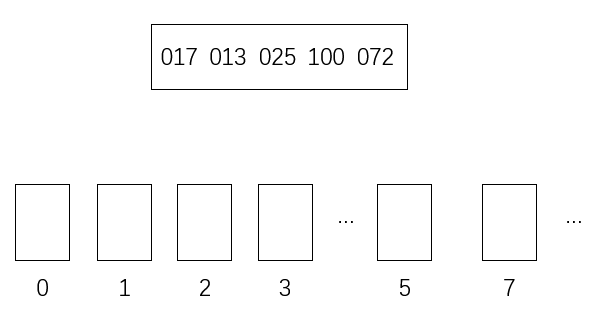
然后，从左到右按个位数将数放入桶里

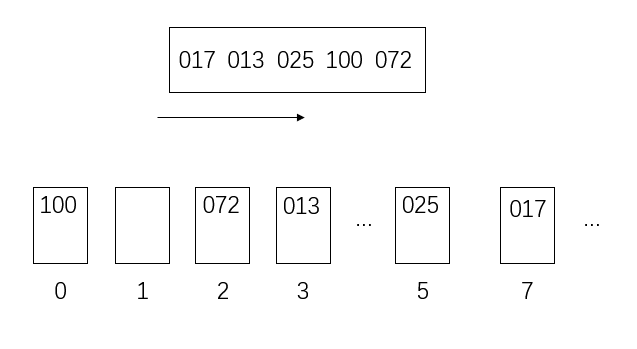
然后把桶里的数从左往右倒出来，数组更新

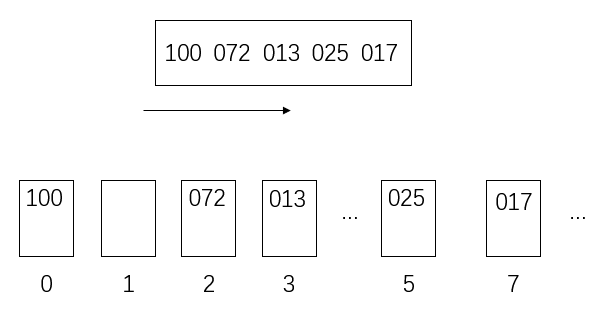
再从左到右按十位数将数放入桶里

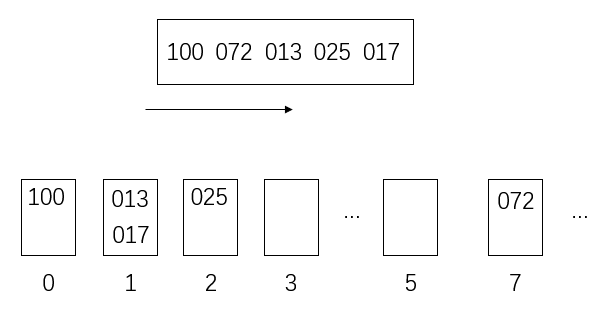
更新

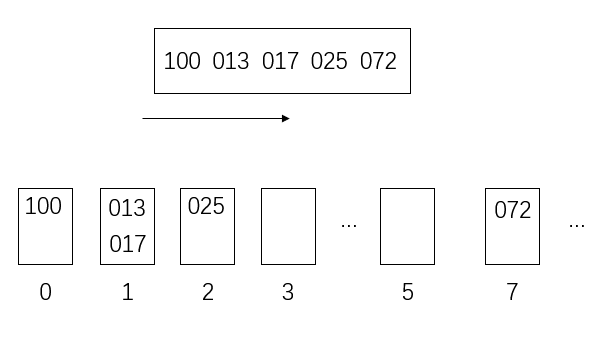
最后按百位数将数放入桶里

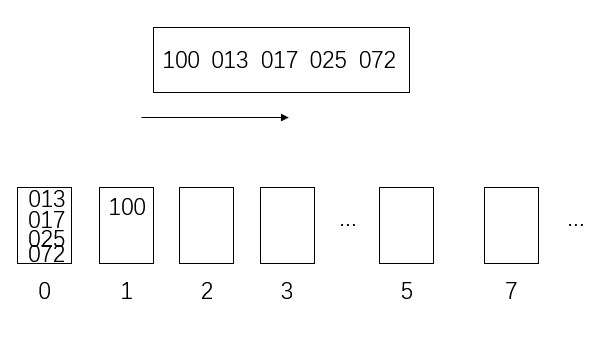
更新

排序结束

因为高位数是晚排序的，所以它优先级就会高，因此就会跑到最右边去

同理可区分十位和个位

代码实现讲解（2:11:25）：https://www.bilibili.com/video/BV13g41157hK?p=5&spm_id_from=333.880.my_history.page.click