【Codeforces717F】Heroes of Making Magic III 线段树 + 找规律

F. Heroes of Making Magic III

time limit per test：3 seconds

memory limit per test：256 megabytes

input：standard input

output：standard output

I’m strolling on sunshine, yeah-ah! And doesn’t it feel good! Well, it certainly feels good for our Heroes of Making Magic, who are casually walking on a one-directional road, fighting imps. Imps are weak and feeble creatures and they are not good at much. However, Heroes enjoy fighting them. For fun, if nothing else.

Our Hero, Ignatius, simply adores imps. He is observing a line of imps, represented as a zero-indexed array of integers a of length n, where ai denotes the number of imps at the i-th position. Sometimes, imps can appear out of nowhere. When heroes fight imps, they select a segment of the line, start at one end of the segment, and finish on the other end, without ever exiting the segment. They can move exactly one cell left or right from their current position and when they do so, they defeat one imp on the cell that they moved to, so, the number of imps on that cell decreases by one. This also applies when heroes appear at one end of the segment, at the beginning of their walk.

Their goal is to defeat all imps on the segment, without ever moving to an empty cell in it (without imps), since they would get bored. Since Ignatius loves imps, he doesn’t really want to fight them, so no imps are harmed during the events of this task. However, he would like you to tell him whether it would be possible for him to clear a certain segment of imps in the above mentioned way if he wanted to.

You are given q queries, which have two types:

• 1 a b k — denotes that k imps appear at each cell from the interval [a, b]
• 2 a b - asks whether Ignatius could defeat all imps on the interval [a, b] in the way described above

Input

The first line contains a single integer n (1 ≤ n ≤ 200 000), the length of the array a. The following line contains n integersa1, a2, ..., an (0 ≤ ai ≤ 5 000), the initial number of imps in each cell. The third line contains a single integer q (1 ≤ q ≤ 300 000), the number of queries. The remaining q lines contain one query each. Each query is provided by integers a, b and, possibly, k(0 ≤ a ≤ b < n, 0 ≤ k ≤ 5 000).

Output

For each second type of query output 1 if it is possible to clear the segment, and 0 if it is not.

Example

input

3
2 2 2
3
2 0 2
1 1 1 1
2 0 2

output

0
1

Note

For the first query, one can easily check that it is indeed impossible to get from the first to the last cell while clearing everything. After we add 1 to the second position, we can clear the segment, for example by moving in the following way: .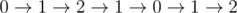

Solution

题目大意：

给定区间[0,N-1]，支持两种操作：

1.区间[l,r]权值+K

2.区间是否可以删光（这里移动时不允许移动到区间之外）

这里可以删光的含义是：从一个格，可以向左/右移动一格，每移动一步，必须使左/右权值-1，当一个地方权值为0时，无法向其移动，删光即能否按照这种移动方式将这个区间中的所有权值删光。

区间上的问题显然可以考虑用线段树来实现。

问题在于这种移动方式，我们不妨考虑其性质。

对于询问一个区间是否能删光，不同的移动方法都有可能能完成，但为了方便我们只考虑其中一种方法。

对于区间$[l,r]$我们从$l$开始移动，我们就先在$l$和$l+1$之间来回，直到$l$清空，我们再在$l+1$和$l+2$之间来回，直到$l+1$清空，如此直到$r-1$和$r$

那么这样能够清空所有位置的权值的条件是：

$$a_{l}>=1$$

$$a_{l+1}-a_{l}>=0$$

$$a_{l+2}-(a_{l+1}-a_{l}+1)>=0$$

$$......$$

那么我们化简一下所有的式子可以得到：

$$a_{l}>=1$$

$$a_{l+1}-a_{l}>=0$$

$$a_{l+2}-a_{l+1}+a_{l}>=1$$

$$......$$

观察一下不等式右边，发现和项数的奇偶有关。

那么我们就可以得到一个通式：

$$a_{r}-a{r-1}+a{r-2}-a_{r-3}+...a_{l}>=[(r-l+1)mod1==0] $$

然后我们很直观的想法就是用线段树去维护这个东西，并且能分奇偶维护更加方便。

问题在于如何维护这个东西，我们做差，另$d_{i}=a_{1}-a{2}+a{3}...$

我们就可以利用这个东西，计算一个区间的值。 所以我们用线段树去维护这个东西。

对于一个区间$[l,r]$这个区间的值$D[l,r]$可以通过$d$来计算

然后我们按照奇偶分别维护，就可以了。

Code

#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
using namespace std;
#define LL long long
inline int read()
{
    int x=,f=; char ch=getchar();
    while (ch<'' || ch>'') {if (ch=='-') f=-; ch=getchar();}
    while (ch>='' && ch<='') {x=x*+ch-''; ch=getchar();}
    return x*f;
}
#define MAXN 300010
#define INF 0x7fffffff
int N,Q,a[MAXN],d[MAXN];
namespace SegmentTree
{
    struct SegmentTreeNode{int l,r,size; LL sum,tag[],D[]; bool f;}tree[MAXN<<];
    #define ls now<<1
    #define rs now<<1|1
    inline void Update(int now,bool o)
    {
        tree[now].D[]=min(tree[ls].D[],tree[rs].D[o]);
        tree[now].D[]=min(tree[ls].D[],tree[rs].D[o^]);
    }
    inline void PushDown(int now,bool o)
    {
        if (tree[now].l==tree[now].r) return;
        if (tree[now].tag[])
            tree[ls].D[]+=tree[now].tag[],tree[ls].tag[]+=tree[now].tag[],
            tree[rs].D[o]+=tree[now].tag[],tree[rs].tag[o]+=tree[now].tag[],
            tree[now].tag[]=;
        if (tree[now].tag[])
            tree[ls].D[]+=tree[now].tag[],tree[ls].tag[]+=tree[now].tag[],
            tree[rs].D[o^]+=tree[now].tag[],tree[rs].tag[o^]+=tree[now].tag[],
            tree[now].tag[]=;
    }
    inline void BuildTree(int now,int l,int r)
    {
        tree[now].l=l; tree[now].r=r; tree[now].size=r-l+;
        if (l==r) {tree[now].D[]=d[l]; tree[now].D[]=INF; return;}
        int mid=(l+r)>>;
        BuildTree(ls,l,mid); BuildTree(rs,mid+,r);
        Update(now,tree[ls].size&);
    }
    inline void Modify(int now,int L,int R,LL x,bool o)
    {
        if (L>R) return;
        int l=tree[now].l,r=tree[now].r;
        PushDown(now,tree[ls].size&);
        if (L<=l && R>=r) {tree[now].tag[o]+=x; tree[now].D[o]+=x; return;}
        int mid=(l+r)>>;
        if (L<=mid) Modify(ls,L,R,x,o);
        if (R>mid) Modify(rs,L,R,x,o^(tree[ls].size&));
        Update(now,tree[ls].size&);
    }
    inline LL Query(int now,int L,int R,bool o)
    {
        if (L>R) return INF;
        int l=tree[now].l,r=tree[now].r;
        PushDown(now,tree[ls].size&);
        if (L<=l && R>=r) return tree[now].D[o];
        int mid=(l+r)>>; LL re=INF;
        if (L<=mid) re=min(re,Query(ls,L,R,o));
        if (R>mid) re=min(re,Query(rs,L,R,o^(tree[ls].size&)));
        return re;
    }
}
using namespace SegmentTree;
int main()
{
    N=read();
    for (int i=; i<=N-; i++) a[i]=read();
    d[]=a[]; for (int i=; i<=N-; i++) d[i]=a[i]-a[i-],a[i]-=a[i-];
    SegmentTree::BuildTree(,,N-);
    Q=read();
    while (Q--)
        {
            int opt=read(),L=read(),R=read(),K;
            if (opt==)
                {
                    K=read(); SegmentTree::Modify(,L,R,K,L&);
                    if ((R-L+)&) SegmentTree::Modify(,R+,N-,-K,(R+)&),SegmentTree::Modify(,R+,N-,K,(R+)&);
                }
            if (opt==)
                {
                    LL x=L>? SegmentTree::Query(,L-,L-,(L-)&):,y=SegmentTree::Query(,R,R,R&);
                    if ((R-L+)&) y+=x; else y-=x;
                    if (y!=((R-L+)&) || SegmentTree::Query(,L,R,L&)+x< || SegmentTree::Query(,L,R,(L&)^)-x<) puts("");
                        else puts("");
                }
//            puts("=========================");
//            for (int i=0; i<=N-1; i++) printf("%I64d    %I64d\n",Query(1,i,i,i&1),Query(1,i,i,(i&1)^1));
//            puts("=========================");
        }
    return ;
}