数据分析---《Python for Data Analysis》学习笔记【03】

《Python for Data Analysis》一书由Wes Mckinney所著，中文译名是《利用Python进行数据分析》。这里记录一下学习过程，其中有些方法和书中不同，是按自己比较熟悉的方式实现的。

第三个实例：US Baby Names 1880-2010

简介： 美国社会保障总署（SSA）提供了一份从1880年到2010年的婴儿姓名频率的数据

数据地址： https://github.com/wesm/pydata-book/tree/2nd-edition/datasets/babynames

准备工作：导入pandas和matplotlib

import pandas as pd
import matplotlib.pyplot as plt
fig,ax=plt.subplots()

我们现在拥有的数据文件是从1880年-2010年的婴儿姓名频率的.txt文件，文件如下所示：

Mary,F,7065
Anna,F,2604
Emma,F,2003
Elizabeth,F,1939
Minnie,F,1746

其中第一列是姓名，第二列是性别，第三列是当年此性别婴儿中取该名字的人数。

文件内容以逗号分隔，因此可以用pandas的read_csv方法读取：

file=pd.read_csv(r"...\yob1880.txt", header=None, names=["Name", "Gender", "Birth"])

现在读取的是1880年的文件，文件没有列名，因此header设为None，同时自己设置列名分别为Name, Gender和Birth。

我们需要给文件加上年份这一列，以便知道某姓名频次是属于哪一年的：

file["Year"]=1880

现在读取的1880年的文件显示如下：

        Name Gender  Birth  Year
0       Mary      F   7065  1880
1       Anna      F   2604  1880
2       Emma      F   2003  1880
3  Elizabeth      F   1939  1880
4     Minnie      F   1746  1880

但是我们有很多份这样的文件，不可能一个一个地手动读取。因此，我们利用循环语句来读取每份文件，并把这些文件用concat命令合并在一起。

file_list=[]  #设置空列表，作为合并列表

for year in range(1880,2011):
    file=pd.read_csv(r"...\yob{}.txt".format(year), header=None, names=["Name", "Gender", "Birth"])
    file["Year"]=year
    file_list.append(file)

data=pd.concat(file_list, ignore_index=True)

concat命令可以把pandas对象按行或列合并起来，命令接收的是一个序列。因此，我们首先设置一个空列表，然后循环读取文件，把文件变为pandas对象，并放入该列表中。这里注意，我们不需要保留原来的索引，因此设置ignore_index参数为True。

接下来，我们就可以开始分析了。

让我们先来看看每一年的男女出生总人数分别是多少。

total_birth=pd.pivot_table(data, values="Birth", index="Year", columns="Gender", aggfunc="sum")

Gender       F       M
Year
1880     90993  110493
1881     91955  100748
1882    107851  113687
1883    112322  104632
1884    129021  114445
1885    133056  107802
1886    144538  110785
1887    145983  101412
1888    178631  120857
1889    178369  110590

用折线图画出来：

ax.plot(range(1880,2011), total_birth["F"], label="Female")
ax.plot(range(1880,2011), total_birth["M"], label="Male")
ax.legend()
ax.set_xticks(range(1880,2021,20))
ax.set_xlim(1880,2020)

plt.show()

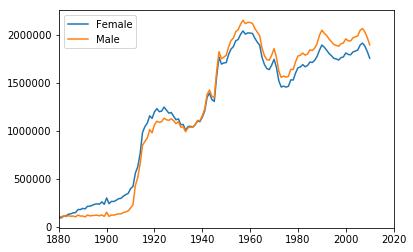
可以看出，每一年男女出生人数都差不多。

接下来，我们想知道某个名字在某年某性别出生婴儿中占比多少。比如：Mary在1880年女性姓名中占比多少，假设结果是0.02，那就说明每100个1880年出生的女婴，有2个被命名为Mary。

我们把女性Mary在1880年对应的出生人数提取出来，然后再把1880年所有女性出生人数提取出来，把两者相除，就得到了（Mary，女，1880年）的百分比。

如果要把所有的姓名百分比计算出来，那么我们可以先把数据按年份和性别分类，然后再用apply方法对所有分类数据进行计算。

把数据按年份和性别分类：

by_year_gender=data.groupby(["Year", "Gender"])

定义apply方法所需的函数（由于该函数比较简单，因此这里直接用lambda函数）：

lambda x: x["Birth"]/x["Birth"].sum()

把函数用于分类数据：

percentage=by_year_gender.apply(lambda x: x["Birth"]/x["Birth"].sum())

percentage的前10行显示如下：

Year  Gender
1880  F       0    0.077643
              1    0.028618
              2    0.022013
              3    0.021309
              4    0.019188
              5    0.017342
              6    0.016177
              7    0.015540
              8    0.014507
              9    0.014155
Name: Birth, dtype: float64

由于percentage的索引和data相同，因此可以直接在data文件上增加一列Percentage：

data["Percentage"]=percentage.values

现在data的前10行如下：

        Name Gender  Birth  Year  Percentage
0       Mary      F   7065  1880    0.077643
1       Anna      F   2604  1880    0.028618
2       Emma      F   2003  1880    0.022013
3  Elizabeth      F   1939  1880    0.021309
4     Minnie      F   1746  1880    0.019188
5   Margaret      F   1578  1880    0.017342
6        Ida      F   1472  1880    0.016177
7      Alice      F   1414  1880    0.015540
8     Bertha      F   1320  1880    0.014507
9      Sarah      F   1288  1880    0.014155

书中使用的是另外一种方法，在定义apply方法所需的函数时，直接在分类数据上加入计算出的百分比数据，这样apply方法可以在保证原数据的前提下把分组后计算出的百分比数据与原数据合并：

def add_percent(group):
    birth=group["Birth"]
    sum=group["Birth"].sum()
    group["Percentage"]=birth/sum
    return group

data=by_year_gender.apply(add_percent)

但是，我们怎么确保各组百分比相加之和等于1呢？这时就需要做一个合理性检查（sanity check）。用numpy的allclose方法来查看每组百分比之和是否接近1：

import numpy as np
print(np.allclose(data.groupby(["Year","Gender"])["Percentage"].sum(),1))

结果显示为True。

在上面的分析过程中，我们发现这个数据文件比较大，为了加速分析进程，我们在这里提取每组（年份+性别）人数最多的前1000名的姓名进行分析：

by_year_gender=data.groupby(["Year", "Gender"])

pieces=[]
for year,group in by_year_gender:
    pieces.append(group.sort_values(by="Birth", ascending=False)[:1000])
top1000=pd.concat(pieces, ignore_index=True)

后续的分析都将针对这个top1000数据集。

接下来让我们选取John，Harry，Mary，Marilyn这几个常见的名字，看一下它们各年份在同性别中占比分别是多少（时间趋势），并用折线图画出来。

fig,ax=plt.subplots(4,1,figsize=(8,8))

pivot=pd.pivot_table(top1000, values="Percentage", index=["Year", "Gender"], columns="Name")

for i, name, gender in zip(range(5),["John", "Harry", "Mary", "Marilyn"],["M","M","F","F"]):
    ax[i].plot(range(1880,2011),pivot["{}".format(name)].unstack()["{}".format(gender)],label="{}".format(name))
    ax[i].legend()

plt.show()

首先，因为选取了4个名字，所以我们把图像分成4个分图。然后，按照年份和性别分组，显示各个名字的百分比，用名字作为列，这样可以很方便地选取数据。最后画图。

图像如下：

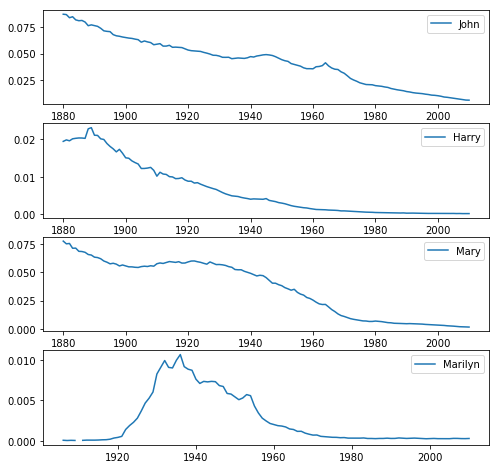
书上用的是这几个名字各年份的总出生人数：

fig,ax=plt.subplots(4,1,figsize=(8,8))

pivot=pd.pivot_table(top1000, values="Birth", index="Year", columns="Name", aggfunc="sum")

for i, name in zip(range(5),["John", "Harry", "Mary", "Marilyn"]):
    ax[i].plot(range(1880,2011),pivot["{}".format(name)],label="{}".format(name))
    ax[i].legend()

plt.show()

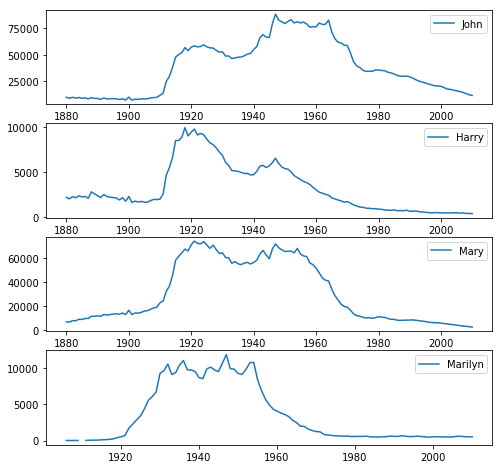
总之，看起来常见的名字越来越不受欢迎了。那么到底是不是这样呢？让我们来验证一下。

把提取出来的排名前1000的名字每年的总占比画出来，如果总占比越来越少，那就说明使用其他名字的比例越来越高（名字越来越多样化）。

import numpy as np

total_percentage=pd.pivot_table(top1000, values="Percentage", index="Year", columns="Gender", aggfunc="sum")

ax.plot(range(1880,2011),total_percentage["F"], label="Female")
ax.plot(range(1880,2011),total_percentage["M"], label="Male")
ax.set_yticks(np.linspace(0,1.2,13))
ax.set_xticks(range(1880,2011,10))
ax.set_xlim(1880,2010)

ax.legend()

plt.show()

还有一种办法是计算总出生人数前50%的不同姓名的数量，如果数量在增加，就说明名字越来越多样化。

这个数据不是那么容易弄出来，让我们先以2010年男宝宝的名字为例，来算一下。

boy2010=top1000[(top1000["Gender"]=="M") & (top1000["Year"]==2010)]
boy2010=boy2010.sort_values(by="Percentage", ascending=False)

boy2010["Percent_Cumsum"]=boy2010["Percentage"].cumsum()
num=boy2010["Percent_Cumsum"].searchsorted(0.5)

首先，提取2010年性别为男的数据，然后按照百分比进行排序，接下来在百分比这一列上使用累计函数cumsum。那么哪里才是百分比累计到50%的地方呢？答案是用searchsorted方法。num显示为116，由于索引是从0开始，因此前117个名字占总出生人数的前50%。

接下来，我们把这一方法扩展到top1000的总体数据上。首先定义apply方法所需的函数，再用apply方法把函数用于整个数据。

def get_percentile_num(group,p=0.5):
    group=group.sort_values(by="Percentage", ascending=False)
    percent_cumsum=group["Percentage"].cumsum()
    num=percent_cumsum.searchsorted(p)
    return num+1

by_year_gender=top1000.groupby(["Year", "Gender"])
percentile_num=by_year_gender.apply(get_percentile_num)

percentile_num=percentile_num.unstack()
percentile_num["F"]=percentile_num["F"].astype(int)
percentile_num["M"]=percentile_num["M"].astype(int)

做完以上这两步后再把数据展开，并转换数据类型。

现在percentile_num的前10行显示如下：

Gender   F   M
Year
1880    38  14
1881    38  14
1882    38  15
1883    39  15
1884    39  16
1885    40  16
1886    41  16
1887    41  17
1888    42  17
1889    43  18

接下来就可以画图了：

ax.plot(range(1880,2011),percentile_num["F"],label="Female")
ax.plot(range(1880,2011),percentile_num["M"],label="Male")
ax.legend()

plt.show()

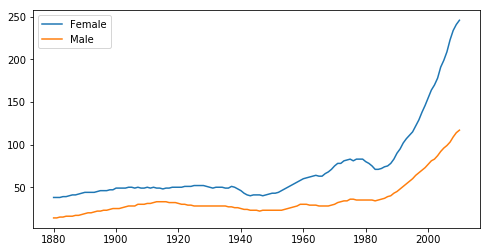
这两种方法都证明随着年份增加，名字越来越多样化了，而且女性的名字多样化程度更甚。

最后一个字母的变革：有研究表明，近百年来，男孩名字的最后一个字母在数量分布上发生了显著变化。那么到底是不是这样呢？

首先提取男孩的名字数据，并在此数据上增加一列：Last_Letter，显示名字的最后一个字母。然后生成一张透视表，按最后一个字母分类，显示每个字母每年在男性名字中的占比。最后，用柱形图画出来。

boy=top1000[top1000["Gender"]=="M"]

boy["Last_Letter"]=boy["Name"].apply(lambda x: x[-1])

letters=pd.pivot_table(boy, values="Percentage", index="Last_Letter", columns="Year", aggfunc="sum")

fig,ax=plt.subplots(figsize=(12,6))

i=0
for year in [1910,1960,2010]:
    ax.bar([j+i for j in range(26)],letters[year],label="{}".format(year), width=-0.3, align="edge")
    i+=0.3
ax.legend()
ax.set_xticks(range(26))
ax.set_xticklabels(letters.index.values)

plt.show()

图像如下：

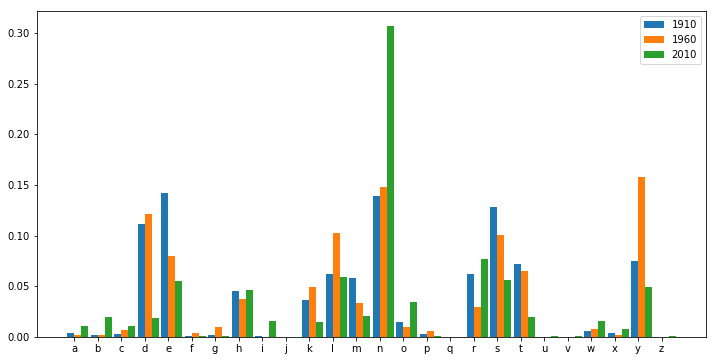
可以看出，最后一个字母为n的男名比例越来越高了。

现在选取尾字母为"d"，"n"，"y"的男孩名字的百分比，并绘制折线图，这样就可以看出其随时间变化的趋势了。

由于我们需要选取字母，因此将letters透视表进行转置，这样就变成了字母为列，年份为行。letters.T的前5行显示如下：

Last_Letter         a         b         c         d         e         f  \
Year
1880         0.006842  0.004516  0.003159  0.083010  0.121664  0.000932
1881         0.007613  0.004665  0.003285  0.083247  0.123139  0.000824
1882         0.006623  0.004407  0.003070  0.084900  0.127658  0.001056
1883         0.007139  0.004272  0.002858  0.084066  0.125831  0.001013
1884         0.007095  0.004247  0.002744  0.085639  0.126803  0.001145   

Last_Letter         g         h         i   j    ...      q         r  \
Year                                             ...
1880         0.001285  0.036554  0.001810 NaN    ...    NaN  0.067326
1881         0.001449  0.037380  0.002045 NaN    ...    NaN  0.072190
1882         0.001240  0.036688  0.001821 NaN    ...    NaN  0.070043
1883         0.001290  0.037465  0.001596 NaN    ...    NaN  0.071680
1884         0.001311  0.036978  0.001381 NaN    ...    NaN  0.078055   

Last_Letter         s         t         u         v         w         x  \
Year
1880         0.166735  0.062755  0.000181  0.000299  0.007629  0.002751
1881         0.162495  0.061818  0.000258  0.000179  0.007424  0.002650
1882         0.160265  0.062109  0.000088  0.000378  0.007653  0.003079
1883         0.158116  0.064359  0.000105  0.000421  0.007589  0.002657
1884         0.154327  0.060973  0.000087  0.000315  0.007217  0.002997   

Last_Letter         y         z
Year
1880         0.075398  0.000262
1881         0.077451  0.000079
1882         0.076966  0.000229
1883         0.079096  0.000115
1884         0.079532  0.000236  

[5 rows x 26 columns]

接下来用d，n，y的数据分别画折线图：

for letter in ["d","n","y"]:
    ax.plot(letters.T.index.values, letters.T[letter], label=letter)
ax.set_xlim(1880,2010)
ax.legend()

plt.show()

男名变女名，女名变男名

有的名字本来是男孩取用的多，但是随着时间的改变，渐渐变成了受女孩欢迎的名字。我们以Lesly相关的名字为例，来看一看这个变化。

首先把Lesly相关的名字提取出来，看看有哪些：

all_names=top1000["Name"].unique()

mask=["lesl" in name.lower() for name in all_names]

lesly_like=all_names[mask]

['Leslie' 'Lesley' 'Leslee' 'Lesli' 'Lesly']

这里提取了lesl开头的名字，一共有5种。

在top1000数据集里提取这5种名字的数据，然后做一个透视表。

filtered=top1000[top1000["Name"].isin (lesly_like)]

table=pd.pivot_table(filtered, values="Birth", index="Year", columns="Gender", aggfunc="sum")

在透视表里增加一列：当年男女出生人数的总和。

table["Sum"]=table["F"]+table["M"]

现在透视表的前5行如下：

Gender     F      M    Sum
Year
1880     8.0   79.0   87.0
1881    11.0   92.0  103.0
1882     9.0  128.0  137.0
1883     7.0  125.0  132.0
1884    15.0  125.0  140.0

按每年男女出生人数比例画图：

ax.plot(table.index.values, table["F"]/table["Sum"], "-", label="Female")
ax.plot(table.index.values, table["M"]/table["Sum"], "--", label="Male")

ax.legend()

plt.show()

图像如下：

由此可以看出，Lesly相关的名字由男名变成了女名。