【欧拉函数】BZOJ4173-数学

【题目大意】

【思路】

基本是popoqqq大爷的题解，稍微添加了几句自己的注释，方便理解

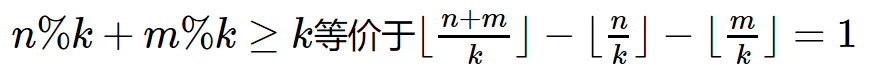
同理，如果n%k+m%k＜k等价于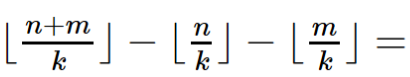0

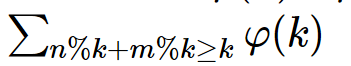
=∑([(n+m)/k]-[n/k]-[m/k])×φ(k) ……因为k不满足条件的时候前面为0

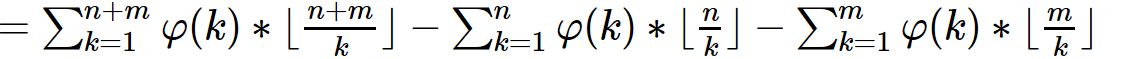……其实右边两个∑也是k=1..(m+n)，但是k>n的时候，[n/k]显然为0，m同理。

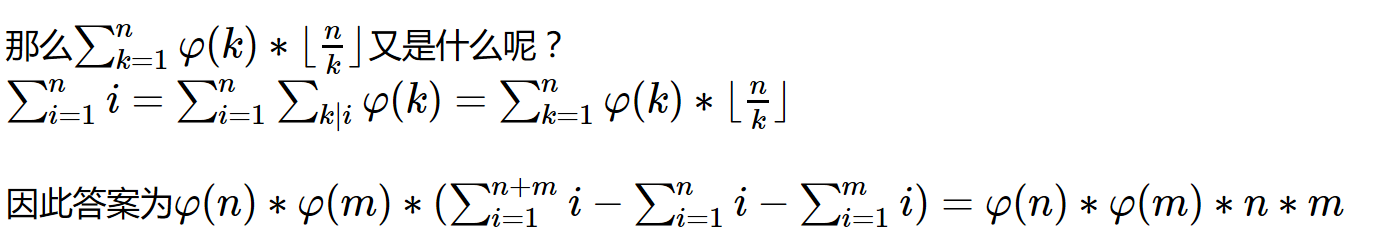
【错误点XXXXD】

……程序烧杯，po也是烧杯。不要忘了ll，不要忘了MOD……

 #include<iostream>
 #include<cstdio>
 #include<algorithm>
 #include<cstring>
 #define MOD 998244353
 using namespace std;
 typedef long long ll;

 ll phi(ll x)
 {
     ll ret=x;
     for (ll i=;i*i<=x;i++)
     {
         if (x%i==)
         {
             ret-=ret/i;
             while (x%i==) x/=i;
         }
     }
     if (x>) ret-=ret/x;
     return ret%MOD;
 }

 void solve()
 {
     ll n,m;
     scanf("%lld%lld",&n,&m);
     printf("%lld",(phi(n)%MOD)*(phi(m)%MOD)%MOD*(n%MOD)%MOD*(m%MOD)%MOD);
 }

 int main()
 {
     solve();
     return ;
 }