最优化问题 Optimization Problems & 动态规划 Dynamic Programming

2018-01-12 22:50:06

一、优化问题

优化问题用数学的角度来分析就是去求一个函数或者说方程的极大值或者极小值，通常这种优化问题是有约束条件的，所以也被称为约束优化问题。

约束优化问题（亦译为受约束的最优化问题）是一类数学最优化问题，它由目标函数以及与目标函数中的变量相关的约束条件两部分组成，优化过程则为在约束条件下最优化（最大化或最小化）目标函数。

经典的优化问题：

• 最短路问题
  
• 旅行商问题（TSP）
• 装箱问题
• 调度问题
• 背包问题

了解并熟练掌握这些经典的优化问题会对以后遇到的新的优化问题有很大的帮助，事实上，很多时候看似是新的问题其实是可以规约（Problem Reduction）到这些经典问题上的，而这些经典的优化问题已经有了非常多的极其完善的解法。

二、动态规划

动态规划（英语：Dynamic programming，简称DP）是一种在数学、管理科学、计算机科学、经济学和生物信息学中使用的，通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。

动态规划背后的基本思想非常简单。大致上，若要解一个给定问题，我们需要解其不同部分（即子问题），再合并子问题的解以得出原问题的解。

动态规划在求解优化问题上非常常用，是一个解决优化问题的利器，其所耗时间往往远少于朴素解法。

动态规划问题的适用条件：

1. 最优子结构性质。如果问题的最优解所包含的子问题的解也是最优的，我们就称该问题具有最优子结构性质（即满足最优化原理）。最优子结构性质为动态规划算法解决问题提供了重要线索；或者说一个问题的最优解可以由其子问题的最优解构建得到。
2. 无后效性。即子问题的解一旦确定，就不再改变，不受在这之后、包含它的更大的问题的求解决策影响。
3. 重叠子问题性质。子问题重叠性质是指在用递归算法自顶向下对问题进行求解时，每次产生的子问题并不总是新问题，有些子问题会被重复计算多次。动态规划算法正是利用了这种子问题的重叠性质，对每一个子问题只计算一次，然后将其计算结果保存在一个表格中，当再次需要计算已经计算过的子问题时，只是在表格中简单地查看一下结果，从而获得较高的效率。

使用斐波那契数列（Fibonacci polynomial）来简单解释一下重叠子问题：

1）自顶向下使用递归实现Fib

def fib(n):
    if n <= 1:
        return n
    else:
        return fib(n-1) + fib(n-2)

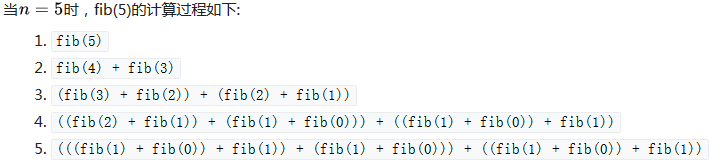
显然，在这种情况下会造成大量的重复计算，这就是重叠子问题。

一个非常正常的想法就是使用memoization，被称为默记法，将第一次计算得到的结果保存下来，之后再需要的时候，就不用重复计算，只需要查表就可以了。

因此这种自顶向下的方法也被称作Table Lookup，查表法。

def fib1(n):
    if not n in memo:
        memo[n] = fib1(n-1) + fib1(n-2)
    return memo[n]
 
memo = {0:0, 1:1}

2）自低向上实现Fib

一般来说，默认动态规划就是使用自低向上来进行迭代计算，这样做的好处是容易理解，且运行效率高。

    int fib2(int n) {
        int d[] = new int[n+1];
        d[0] = 0;
        d[1] = 1;
        for (int i = 2; i <= n; i++) {
            d[i] = d[i - 1] + d[i - 2];
        }
        return d[n];
    }

一些理解：

1、动态规划算法本质上也是一种用空间换时间的算法

2、不要被指数复杂度的问题吓到，往往我们可以找到更快的解法

3、动态规划有非常广泛的应用场景，一般来说，遇到递归问题，都可以考虑一下是否可以使用动态规划来提高运行效率

4、要学会规约，将其他的一些问题规约到经典的优化问题上简化解决步骤

5、Dynamic Problem由Bellman发明，不用纠结于为什么要使用Dynamic这个词来命名，因为本身就只是个名称。动态规划就是使用保存递归时的结果，因而不会在解决同样的问题时花费时间，来对原问题进行优化