《用 Python 学微积分》笔记 2

《用 Python 学微积分》原文见参考资料 1。

13、大 O 记法

比较两个函数时，我们会想知道，随着输入值 x 的增长或减小，两个函数的输出值增长或减小的速度究竟谁快谁慢。通过绘制函数图，我们可以获得一些客观的感受。

比较 x!、e^x、x³ 和 log(x) 的变化趋势。

import numpy as np
import sympy
import matplotlib.pyplot as plt

x = range(1,7)
factorial = [np.math.factorial(i) for i in x]
exponential = [np.e**i for i in x]
polynomial = [i**3 for i in x]
logarithmic = [np.log(i) for i in x]

plt.plot(x,factorial,'black',\
         x,exponential, 'blue',\
         x,polynomial, 'green',\
          x,logarithmic, 'red')

plt.show()

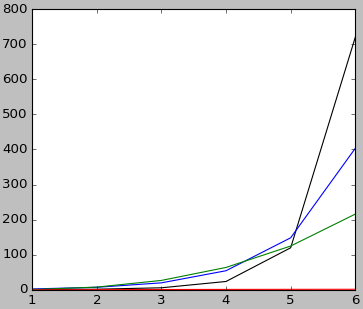
根据上图，当 x—>∞ 时，x!>e^x>x³>ln(x)。要想证明的话，可以取极限，用洛必达法则，例如：

$$\lim_{x\rightarrow \infty}\frac{e^x}{x^3}=\infty$$

表明当 x—>∞ 时，虽然分子分母都在趋向无穷大，但分子远远凌驾于分母之上。类似地，也可以这样看：

$$\lim_{x\rightarrow \infty}\frac{ln(x)}{x^3}=0$$

表明分母远远凌驾于分子之上。

SymPy 是 Python 的数学符号计算库，用它可以进行数学公式的符号推导。下面代码用 SymPy 来推导上面两式。

import sympy
from sympy.abc import x
# sympy中无限infty用oo表示
print ((sympy.E**x)/(x**3)).limit(x,sympy.oo)
# result is: oo
print (sympy.ln(x)/x**3).limit(x,sympy.oo)
# result is 0

为了描述这种随着 x—>∞ 或 x—>0 时函数的表现，我们定义如下大 O 记法：

若我们称函数 f(x) 在 x—>0 时是 O(g(x))，则需要找到一个常数 C，对于所有足够小的 x，均有 |f(x)|<C|g(x)|。

若我们称函数 f(x) 在 x—>∞ 时是 O(g(x))，则需要找到一个常数 C，对于所有足够大的 x，均有 |f(x)|<C|g(x)|。

之所以叫大 O 记法，是因为函数的增长速率很多时候被称为函数的阶（Order）。

例如，当 x—>∞ 时，x(1+x²)^1/2 是 O(x²)，下面来个直观感受。

下图是两个函数的变化趋势，红线是 x(1+x²)^1/2 ，蓝线是 2x² 。

import sympy
from sympy.abc import x
import numpy as np
import matplotlib.pyplot as plt

xvals = np.linspace(0,100,1000)
f = x*sympy.sqrt(1+x**2)
g = 2*x**2
y1 = [f.evalf(subs={x:xval}) for xval in xvals]
y2 = [g.evalf(subs={x:xval}) for xval in xvals]
plt.plot(xvals[:10],y1[:10],'r',xvals[:10],y2[:10],'b')
#plt.plot(xvals,y1,'r',xvals,y2,'b')
plt.show()

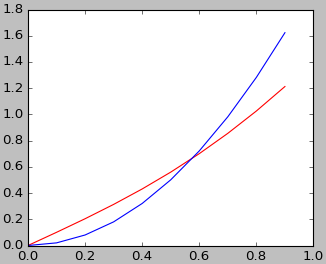
Sympy 可以帮助我们分析函数的阶，如下面求 x(1+x²)^1/2 的阶。

import sympy
from sympy.abc import x

f = x*sympy.sqrt(1+x**2)
print sympy.O(f, (x, sympy.oo))
# result is : O(x**2, (x, oo))

计算机中使用大 O 记法，通常是分析当输入数据 —>∞ 时，程序在时间或空间上的表现。然而，从上面的介绍，我们知道这个位置可以是 0，甚至可以是任何有意义的位置。

import sympy
from sympy.abc import x

f = x*sympy.sqrt(1+x**2)
print sympy.O(f, (x, 0))
# result is : O(x)

在前面泰勒级数一节，利用 Sympy 取函数泰勒级数的前几项时，代码是这样：

import sympy
from sympy.abc import x

exp = sympy.E**x
sum15 = exp.series(x,0,15).removeO()
print sum15

其中 removeO() 的作用是让 sympy 忽略掉级数展开后的大 O 表示项。不然结果如下：

import sympy
from sympy.abc import x

exp = sympy.E**x
print exp.series(x, 0, 3)
# result is: 1 + x + x**2/2 + O(x**3)

这表示从泰勒级数的第 4 项起，剩余所有项在 x—>0 时是 O(x³)。这表明，当 x—>0 时，用 1+x+0.5x² 来近似 e^x ，我们得到的误差上限将是 Cx³，其中 C 是一个常数。也就是说，大 O 记法能用来描述我们使用多项式近似时的误差。

另外大 O 记法也可以直接参与计算中去，例如要计算：

$$cos(x^2)\sqrt{(x)}$$

在 x—>0 时阶 O(x⁵) 以内的多项式近似，可以这样：

$$cos(x^2)\sqrt{(x)}=(1-\frac{1}{2}x^4+O(x^6))x^{\frac{1}{2}}$$

$$\qquad = x^{\frac{1}{2}}-    \frac{1}{2}x^{\frac{9}{2}} + O(x^{\frac{13}{2}})$$

import sympy
from sympy.abc import x

print (sympy.cos(x**2)*sympy.sqrt(x)).series(x,0,5)
# result is: sqrt(x) - x**(9/2)/2 + O(x**5)

14、导数

对函数某一点求导，得到的是函数在该点处切线的斜率。选中函数图像中某一点，不断放大，最后会发现函数图像一条直线，这条直线就是切线。下面获得一些直观的感受。

import numpy as np
from sympy.abc import x
import matplotlib.pyplot as plt

# 函数
f = x**-*x-
# 在x=6处正切于函数的切线
line = *x-

d1 = np.linspace(,,)
d2 = np.linspace(,,)
d3 = np.linspace(,,)
d4 = np.linspace(5.8,6.2,)
domains = [d1,d2,d3,d4]

# 画图的函数
def makeplot(f,l,d):
    plt.plot(d,[f.evalf(subs={x:xval}) for xval in d],'b',\
             d,[l.evalf(subs={x:xval}) for xval in d],'r')

for i in range(len(domains)):
    # 绘制包含多个子图的图表
    plt.subplot(, , i+)
    makeplot(f,line,domains[i])

plt.show()

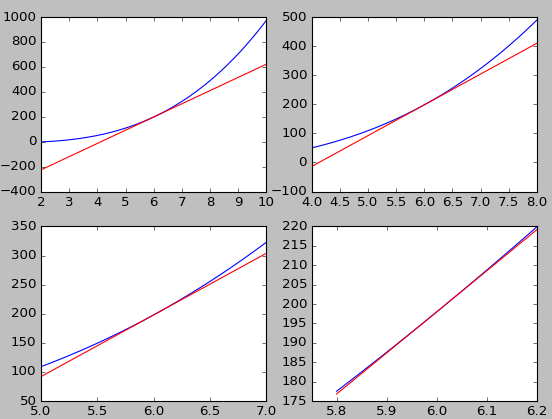
导数定义 1：

$$f'(a)=\frac{df}{dx}\bigg|_{x=a}=\lim_{x\rightarrow a}\frac{f(x)-f(a)}{x-a}$$

若该极限不存在，则函数在 x=a 处的导数不存在。

导数定义 2：

$$f'(a)=\frac{df}{dx}\bigg|_{x=a}=\lim_{h\rightarrow 0}\frac{f(a+h)-f(a)}{h}$$

若该极限不存在，则函数在 x=a 处的导数不存在。

导数定义 3：

函数 f(x) 在 x=a 处的导数 f'(a) 是满足如下条件的常数 C，对于在 a 附近输入值的微小变化 h，有 f(a+h)=f(a)+Ch+O(h²) 始终成立。也就是说导数 C 输入值变化中一阶项的系数。上式稍加变化，两边同时除以 h，并同时取极限可得：

$$\lim_{h\rightarrow 0}\frac{f(a+h)-f(a)}{h}=\lim_{h\rightarrow 0}C+O(h)=C$$

便与上面定义 2 相一致了。

例如求 cos(x) 在 x=a 处的导数：

$$cos(a+h)=cos(a)cos(h)-sin(a)sin(h)$$

$$\qquad = cos(a)(1+O(h^2))-sin(a)(h+O(h^3))$$

$$\qquad = cos(a)-sin(a)h +O(h^2)$$

所以：

$$\frac{d}{dx}{cos(x)}\bigg|_{x=a}=-sin(a)$$

我们可以自己定义求导的函数：

import numpy as np
from sympy.abc import x

f = lambda x: x**3-2*x-6
# 我们设定参数h的默认值，如果调用函数时没有指明参数h的值，便会使用默认值
def derivative(f,h=0.00001):
    return lambda x: float(f(x+h)-f(x))/h
fprime = derivative(f)
print fprime(6)
# result is：106.000179994

Sympy 也提供求导的方法：

from sympy.abc import x

f = x**3-2*x-6
print f.diff()
# result is :3*x**2 - 2
print f.diff().evalf(subs={x:6})
# result is : 106.0000000000

依据导数的定义 3，有  f(a+h)=f(a)+f'(a)h+O(h²)，如果将高阶项丢掉，就获得了 f(a+h) 的线性近似式子：f(a+h)≈f(a)+f'(a)h。

例如，用线性近似的方法估算 255^1/2：

$$\sqrt{256-1}\approx \sqrt{256}+\frac{1}{2\sqrt{256}}(-1)$$

$$\qquad = 16 - \frac{1}{32}$$

$$\qquad = 15\frac{31}{32}$$

15、牛顿迭代法

如何在不使用 x^1/2 前提下求 C 的正二次根。

上述问题等价于求 f(x)=x²+C=0 的解，根据上面介绍的线性近似：f(x+h)≈f(x)+f'(x)h 。如果 f(x+h)=0，那么：

$$h\approx -\frac{f(x)}{f'(x)}$$

$$x+h\approx x - \frac{f(x)}{f'(x)}$$

如果我们对 f(x)=0 的解有一个初始估计 x₀，便可以用上面的近似不断获取更加准确的估计值，方法为：

$$x_{n+1} = x_{n} - \frac{f(x_n)}{f'_{x_n}}$$

将 f(x)=x²+C 代入上式，即得 x_n 的更新规则：

$$x_{n+1} = \frac{1}{2}(x_{n}+\frac{C}{x_{n}})$$

from sympy.abc import x

def mysqrt(c, x = 1, maxiter = 10, prt_step = False):
    for i in range(maxiter):
        x = 0.5*(x+ c/x)
        if prt_step == True:
            # 在输出时，{0}和{1}将被i+1和x所替代
            print "After {0} iteration, the root value is updated to {1}".format(i+1,x)
    return x

print mysqrt(2,maxiter =4,prt_step = True)
# After 1 iteration, the root value is updated to 1.5
# After 2 iteration, the root value is updated to 1.41666666667
# After 3 iteration, the root value is updated to 1.41421568627
# After 4 iteration, the root value is updated to 1.41421356237
# 1.41421356237

通过绘图进一步了解这个方法，例如，我们要猜 f(x)=x²-2x-4=0 的解，从 x₀=2 开始，找到 f(x) 在 x=x₀ 处的切线 y=2x-8，找到其与 y=0 的交点 (4,0)，将该交点作为新的猜测解 x₁=4，如此循环。

import numpy as np
import matplotlib.pyplot as plt

f = lambda x: x**2-2*x-4
l1 = lambda x: 2*x-8
l2 = lambda x: 6*x-20

x = np.linspace(0,5,100)

plt.plot(x,f(x),'black')
plt.plot(x[30:80],l1(x[30:80]),'blue', linestyle = '--')
plt.plot(x[66:],l2(x[66:]),'blue', linestyle = '--')

l = plt.axhline(y=0,xmin=0,xmax=1,color = 'black')
l = plt.axvline(x=2,ymin=2.0/18,ymax=6.0/18, linestyle = '--')
l = plt.axvline(x=4,ymin=6.0/18,ymax=10.0/18, linestyle = '--')

plt.text(1.9,0.5,r"$x_0$", fontsize = 18)
plt.text(3.9,-1.5,r"$x_1$", fontsize = 18)
plt.text(3.1,1.3,r"$x_2$", fontsize = 18)

plt.plot(2,0,marker = 'o', color = 'r' )
plt.plot(2,-4,marker = 'o', color = 'r' )
plt.plot(4,0,marker = 'o', color = 'r' )
plt.plot(4,4,marker = 'o', color = 'r' )
plt.plot(10.0/3,0,marker = 'o', color = 'r' )

plt.show()

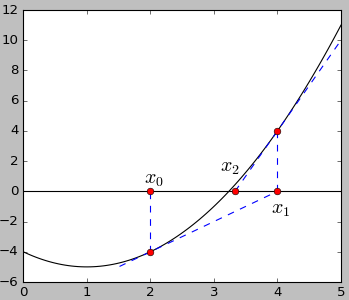
如下定义牛顿迭代法：

def NewTon(f, s = 1, maxiter = 100, prt_step = False):
    for i in range(maxiter):
        # 相较于f.evalf(subs={x:s}),subs()是更好的将值带入并计算的方法。
        s = s - f.subs(x,s)/f.diff().subs(x,s)
        if prt_step == True:
            print "After {0} iteration, the solution is updated to {1}".format(i+1,s)
    return s

from sympy.abc import x
f = x**2-2*x-4
print NewTon(f, s = 2, maxiter = 4, prt_step = True)
# After 1 iteration, the solution is updated to 4
# After 2 iteration, the solution is updated to 10/3
# After 3 iteration, the solution is updated to 68/21
# After 4 iteration, the solution is updated to 3194/987
# 3194/987

Sympy 可以帮助我们求解方程：

import sympy
from sympy.abc import x
f = x**2-2*x-4
print sympy.solve(f,x)
# result is：[1 + sqrt(5), -sqrt(5) + 1]

参考资料：

[1] https://ryancheunggit.gitbooks.io/calculus-with-python/content/