C++使用回溯法实现N皇后问题的求解

回溯法是个很无聊的死算方法，没什么技巧，写这篇博客主要原因是以前思路不太清晰，现在突然想用回溯法解决一个问题时，无法快速把思路转换成代码。

-------------------------------------------------------------------------------------------------------------------------------------

N-皇后问题描述：在N*N的棋盘上，每一行放置一个皇后，使得任意皇后之间不能互相攻击。求放置方法。

（因为国际象棋中皇后可以走横竖斜线，所以相当于是任意2个棋子不处在同一行、列或对角线）

思路是设解为四维向量x，第i行把皇后放在第x[i]列。（这里把行号列号均从0开始）然后像下面这样一个个找：

初始：x为空。令x[0] = 0，然后寻找第1个符合约束（简称“合法”）的x[1]，可得x[1] = 2。再寻找第1个合法的x[2]，发现无论是0、1、2、3都不行。于是就得回退了。

退到x[1]，寻找下一个符合约束的x[1]，即令x[1]=3，再继续找x[2]。若找到一组解则回退，寻找下一组解，一直到无法回退为止。

（比如x = { 1, 3, 0, 2 }，添加x到解集中，之后回退寻找下一个合法的x[2]。此时发现1、2、3都不行，于是再回退，寻找下一个合法的x[1]。）

#include <stdio.h>
#include <vector>
#include <array>
using namespace std;

template <int N>
class QueenProblem
{
public:
	explicit QueenProblem()
	{
		for (int i = 0; i < N; i++)
			x[i] = -1;
		run();
	}

	size_t size() const { return results.size(); }
	const array<int, N>& operator[](size_t k) const { return results[k]; }

private:
	vector<array<int, N>> results; // 解集

	// 解向量, (i,x[i])代表第i行第x[i]列放置皇后
	// 其中行号和列号都是从0开始, 即范围为[0,N)
	// x[i]=-1则代表第i行的位置并未确定
	array<int, N> x;

	void run()
	{
		int k = 0;
		while (k >= 0)
		{
			x[k]++; // 尝试新的位置
			while (x[k] < N && !CheckRow(k))
				x[k]++;

			if (x[k] == N) // 当前行无法放置皇后, 回溯
			{
				x[k--] = -1;
				continue;
			}

			if (k == N - 1)  // 找到一组解, 将其添加到解集中并回溯寻找新的解
			{
				results.emplace_back(x);
				x[k--] = -1;
			}
			else // 第0到k行合法, 尝试设置第k+1行的皇后
			{
				k++;
			}
		}
	}

	// 假设第0到k-1行均成功放置皇后并且合法(即其中任意2个皇后不处于同一行/列/对角线)
	// 判断第k行的放置方案是否合法, 若合法则返回true, 否则返回false
	bool CheckRow(int k)
	{
		for (int i = 0; i < k; i++)
			if (x[i] == x[k] || abs(x[i] - x[k]) == abs(i - k))
				return false;
		return true;
	}
};

int main()
{
#define PrintNQueenSolNum(N) printf("%2d皇后的解的数量: %7ld\n", N, \
                               QueenProblem<N>().size());
	PrintNQueenSolNum(1);
	PrintNQueenSolNum(2);
	PrintNQueenSolNum(3);
	PrintNQueenSolNum(4);
	PrintNQueenSolNum(5);
	PrintNQueenSolNum(6);
	PrintNQueenSolNum(7);
	PrintNQueenSolNum(8);
	PrintNQueenSolNum(9);
	PrintNQueenSolNum(10);
	PrintNQueenSolNum(11);
	PrintNQueenSolNum(12);
	PrintNQueenSolNum(13);
	PrintNQueenSolNum(14);
	PrintNQueenSolNum(15);
	printf("其中, 4皇后的解为:\n");
	QueenProblem<4> sol;
	for (size_t i = 0; i < sol.size(); i++)
	{
		printf("第%d组解: ", i);
		for (int x : sol[i])
			printf("%d ", x);
		printf("\n");
	}
	return 0;
}

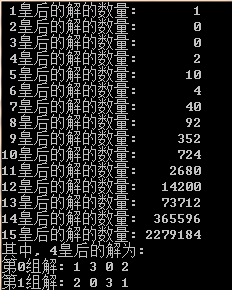
直接贴包装后的代码了，编译期确定N，所以不支持运行时确定N是多少。算到15皇后就完了。

体现回溯法的核心代码就是成员函数run()