【排序】堆排序，C++实现

原创文章，转载请注明出处！

博客文章索引地址

博客文章中代码的github地址

# 预备知识

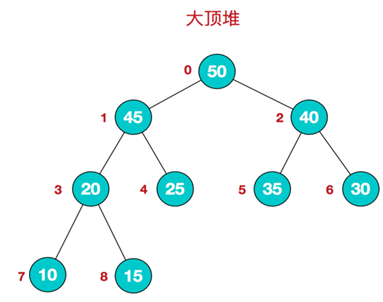
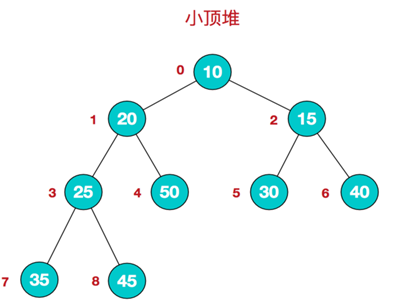
    堆是一种特殊的树形数据结构，即完全二叉树。堆分为大根堆和小根堆，大根堆为根节点的值大于两个子节点的值；小根堆为根节点的值小于两个子节点的值，同时根节点的两个子树也分别是一个堆。

# 基本思路

• 步骤一：建立大根堆--将n个元素组成的无序序列构建一个大根堆，
• 步骤二：交换堆元素--交换堆尾元素和堆首元素，使堆尾元素为最大元素；
• 步骤三：重建大根堆--将前n-1个元素组成的无序序列调整为大根堆

重复执行步骤二和步骤三，直到整个序列有序。

# 图示说明

• 步骤一：建立大根堆

① 无序序列建立完全二叉树

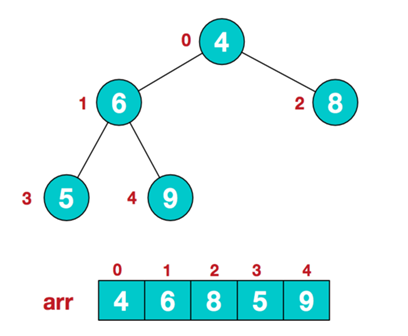
② 从最后一个叶子节点开始，从左到右，从下到上调整，将完全二叉树调整为大根堆

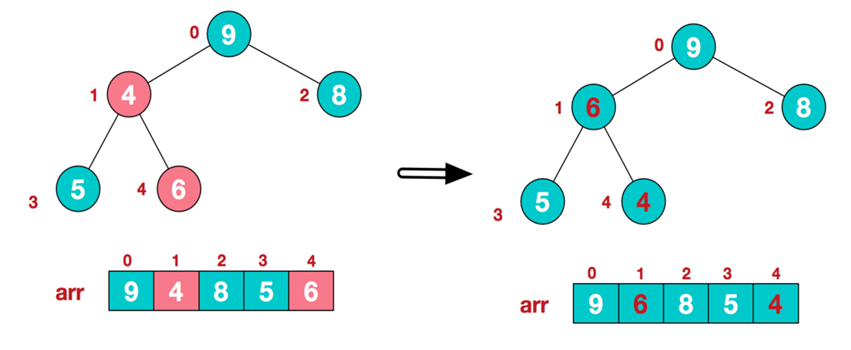
a.找到第1个非叶子节点6，由于6的右子节点9比6大，所以交换6和9。交换后，符合大根堆的结构。

c.找到第2个非叶子节点4，由于的4左子节点9比4大，所以交换4和9。交换后不符合大根堆的结构，继续从右到左，从下到上调整。

• 步骤二：交换堆元素（交换堆首和堆尾元素--获得最大元素）

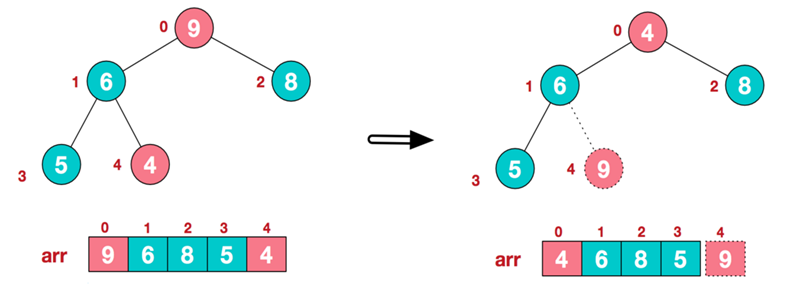
• 步骤三：重建大根堆（前n-1个元素）

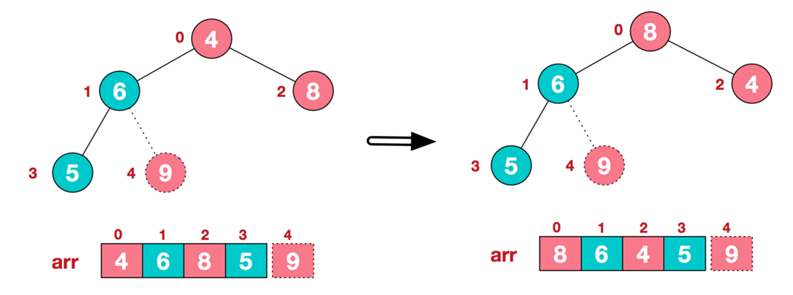
• 重复执行步骤二和步骤三，直到整个序列有序

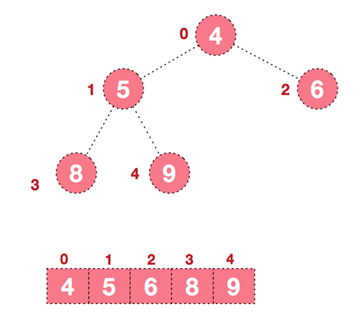
# C++代码

#include<iostream>
#include<vector>
using namespace std;

// 递归方式构建大根堆(len是arr的长度，index是第一个非叶子节点的下标)
void adjust(vector<int> &arr, int len, int index)
{
    int left = 2*index + 1; // index的左子节点
    int right = 2*index + 2;// index的右子节点

    int maxIdx = index;
    if(left<len && arr[left] > arr[maxIdx])     maxIdx = left;
    if(right<len && arr[right] > arr[maxIdx])     maxIdx = right;

    if(maxIdx != index)
    {
        swap(arr[maxIdx], arr[index]);
        adjust(arr, len, maxIdx);
    }

}

// 堆排序
void heapSort(vector<int> &arr, int size)
{
    // 构建大根堆（从最后一个非叶子节点向上）
    for(int i=size/2 - 1; i >= 0; i--)
    {
        adjust(arr, size, i);
    }

    // 调整大根堆
    for(int i = size - 1; i >= 1; i--)
    {
        swap(arr[0], arr[i]);           // 将当前最大的放置到数组末尾
        adjust(arr, i, 0);              // 将未完成排序的部分继续进行堆排序
    }
}

int main()
{
    vector<int> arr = {8, 1, 14, 3, 21, 5, 7, 10};
    heapSort(arr, arr.size());
    for(int i=0;i<arr.size();i++)
    {
        cout<<arr[i]<<endl;
    }
    return 0;
}

　　

# 参考文献：

文中配图参考地址