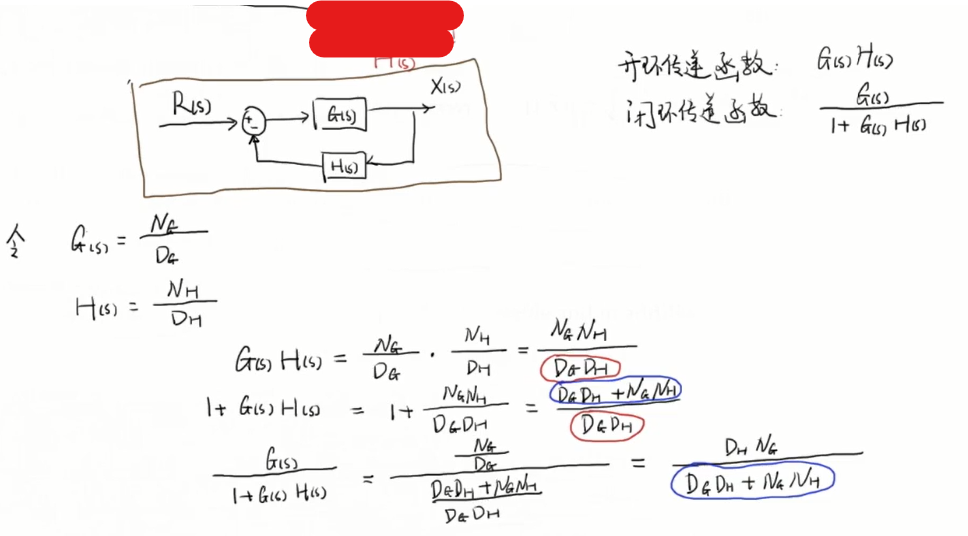
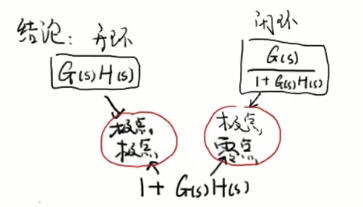
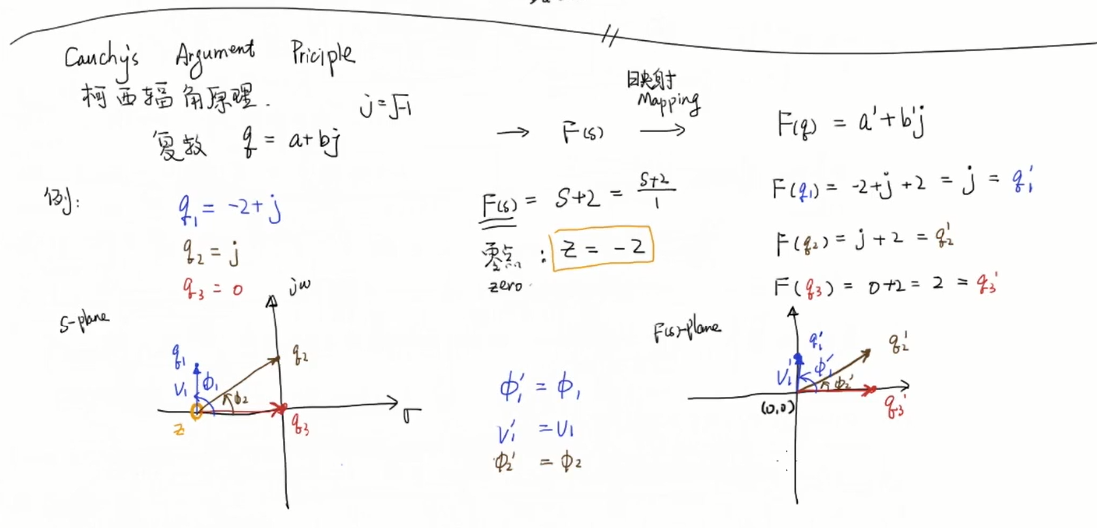
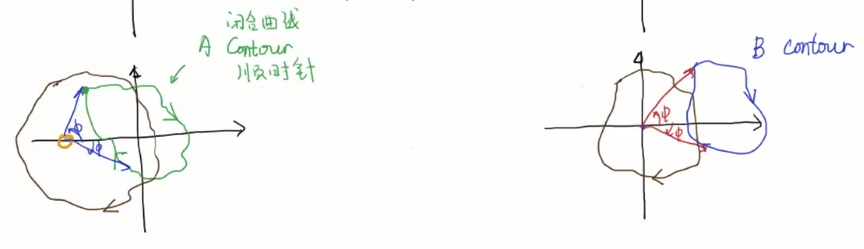
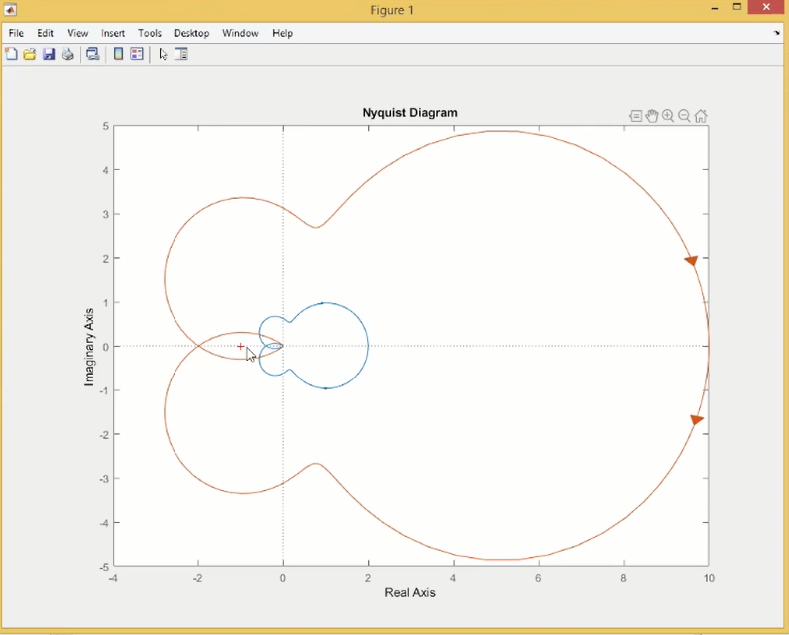
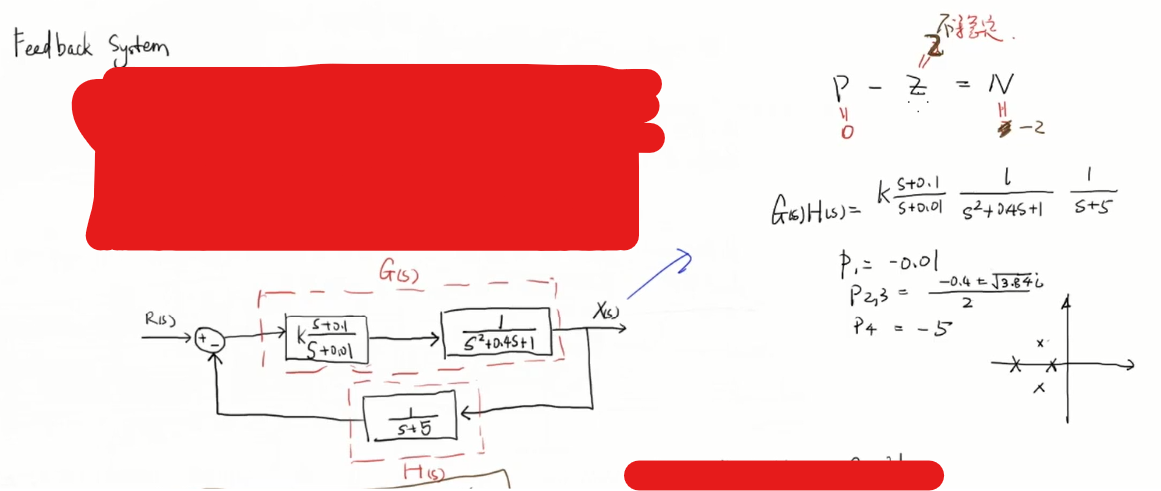
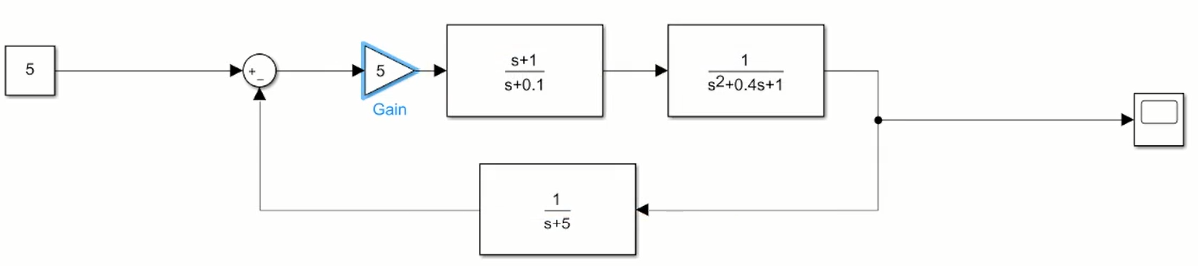
A曲线内有4个极点两个零点，则B曲线绕（0,0）逆时针两圈

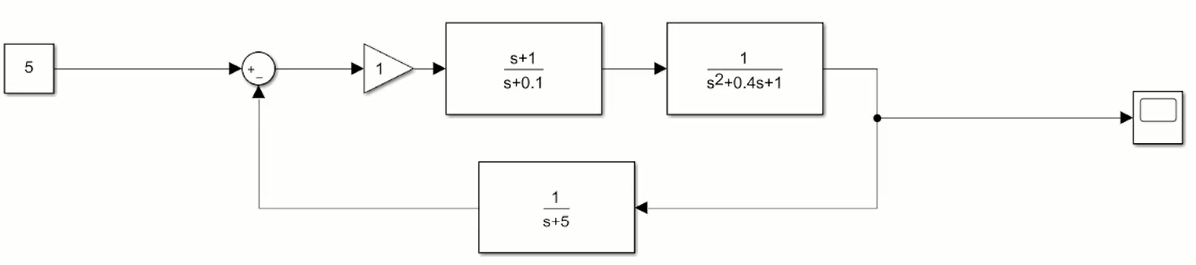
A曲线是nyqyict contour中的曲线，P是A曲线内的（）极点个数，Z是（）极点个数，N是曲线B逆时针围绕（-1,0）的圈数

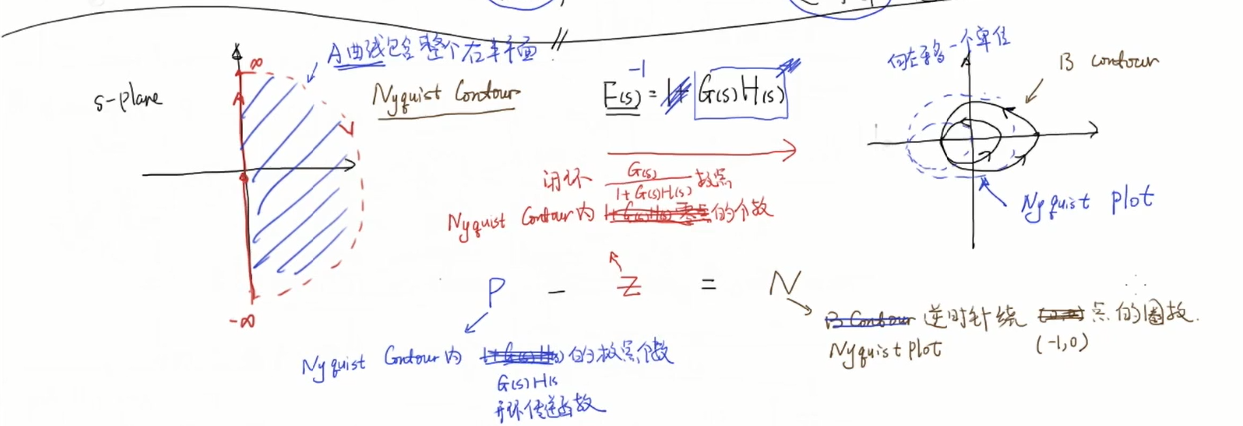
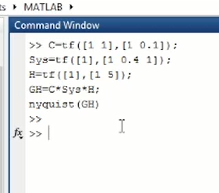
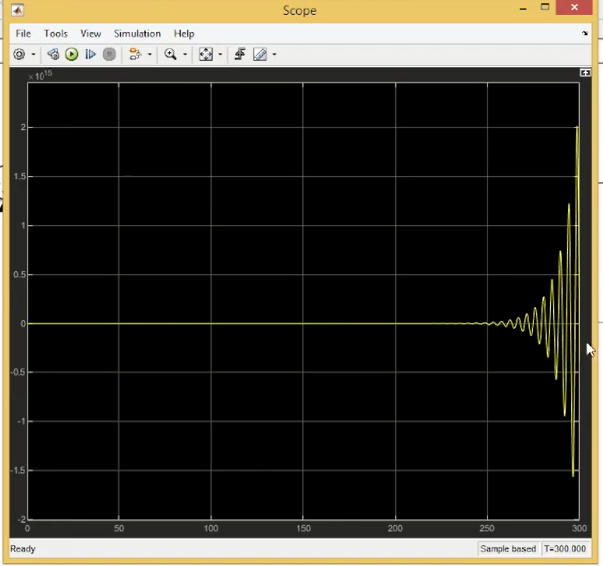
没过（-1,0）点所以z=0

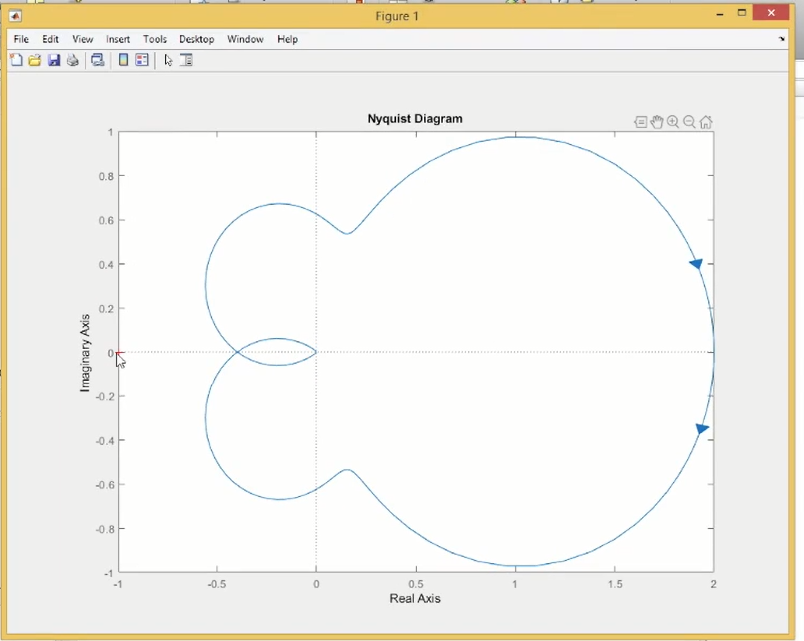
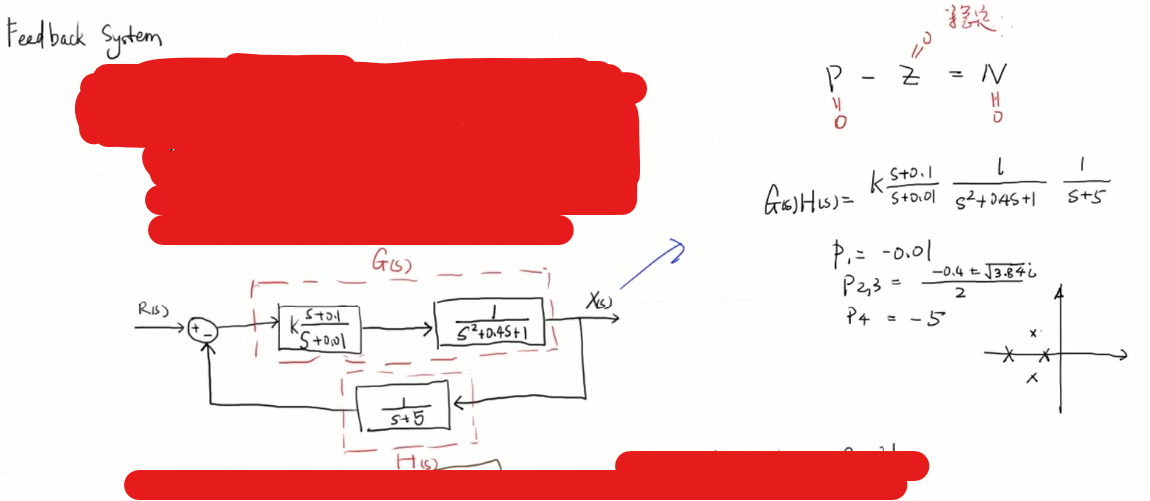
13_奈奎斯特稳定性判据_Nyquist Stability Criterion_Part 1的更多相关文章

  1. 奈奎斯特定理 and 香农定理

    -----------------------整理自<21ic电子网> 奈奎斯特定理(Nyquist's Theorem)和香农定理(Shannon's Theorem)是网络传输中的两个 ...

  2. 奈奎斯特采样定理（Nyquist）

    采样定理在1928年由美国电信工程师H.奈奎斯特首先提出来的,因此称为奈奎斯特采样定理. 1933年由苏联工程师科捷利尼科夫首次用公式严格地表述这一定理,因此在苏联文献中称为科捷利尼科夫采样定理. 1 ...

  3. 一篇对iOS音频比较完善的文章

    转自:http://www.cnblogs.com/iOS-mt/p/4268532.html 感谢作者:梦想通 前言 从事音乐相关的app开发也已经有一段时日了,在这过程中app的播放器几经修改我也 ...

  4. C++面试题汇集

    1.在C++ 程序中调用被C 编译器编译后的函数,为什么要加extern “C”?答:首先,extern是C/C++语言中表明函数和全局变量作用范围的关键字,该关键字告诉编译器,其声明的函数和变量可以 ...

  5. 数字信号处理--Z变换，傅里叶变换，拉普拉斯变换

    傅立叶变换.拉普拉斯变换.Z变换最全攻略 作者:时间:2015-07-19来源:网络       傅立叶变换.拉普拉斯变换.Z变换的联系?他们的本质和区别是什么?为什么要进行这些变换.研究的都是什么? ...

  6. ASIO插件 真的能提升 音质？(听音乐者必看)

    最近在倒弄HIFI音乐播放器footbar2000的配置时,发现了2011年的一个神贴, 最牛逼的是,这个神贴到现在还屹立不倒,还有很多无知的人在下面膜拜, 我真的想问:你这么优秀,都能逆天反转音质, ...

  7. PCM-脉码调制

    1. PCM---Pulse Code Modulation,脉码调制.       在光纤通信系统中,光纤中传输的是二进制光脉冲“0”码和“1”码,它由二进 脉冲编码调制 制数字信号对光源进行通断调 ...

  8. 电赛总结（四）——波形发生芯片总结之AD9854

    一.特性参数 ·300M内部时钟频率 ·可进行频移键控(FSK),二元相移键控(BPSK),相移键控(PSK),脉冲调频(CHIRP),振幅调制(AM)操作 ·正交的双通道12位D/A转换器 ·超高速 ...

  9. ADC驱动器或差分放大器设计指南

    作为应用工程师,我们经常遇到各种有关差分输入型高速模数转换器(ADC)的驱动问题.事实上,选择正确的ADC驱动器和配置极具挑战性.为了使鲁棒性ADC电路设计多少容易些,我们汇编了一套通用“路障”及解决 ...

随机推荐

  1. linux中()、[]、{}、(())、[[]]等各种括号的使用

    转至:https://www.jianshu.com/p/b88c7e07aaa9 linux中().[].{}.(()).[[]]等各种括号的使用 1.小括号.圆括号() 1.1 单小括号() 命令 ...

  2. LeetCode-081-搜索旋转排序数组 II

    搜索旋转排序数组 II 题目描述:已知存在一个按非降序排列的整数数组 nums ,数组中的值不必互不相同. 在传递给函数之前,nums 在预先未知的某个下标 k(0 <= k < nums ...

  3. 国产化之Arm64 CPU+银河麒麟系统安装.NetCore

    背景 某个项目需要实现基础软件全部国产化,其中操作系统指定银河麒麟,银河麒麟就是一个Linux发行版,数据库使用达梦V8,这个数据库很多概念和Oracle相似,CPU平台的范围:龙芯.飞腾.鲲鹏等. ...

  4. 矩池云上安装yolov4 darknet教程

    这里我是用PyTorch 1.8.1来安装的 拉取仓库 官方仓库 git clone https://github.com/AlexeyAB/darknet 镜像仓库 git clone https: ...

  5. 调用Visual Studio的cl.exe编译C/C++程序

    @ 目录 调用Visual Studio的cl.exe编译C/C++程序 前言 1.查看VS的路径 2.添加环境变量 3.查看设置是否生效 4.配置Notepad++ 调用Visual Studio的 ...

  6. centos7运行system-config-kickstart时报错

    centos7运行system-config-kickstart时在Package Selection模块中出现如下错误: Package Selection Packageselection is ...

  7. 快速整明白Redis中的整数集合到底是个啥

    整数集合简介 整数集合(intset)是Redis集合数据类型的内部编码之一,当集合数据类型中的元素都是整数并且元素数量较少的时候,Redis就使用整数集合作为内部编码. 整数集合(intset)中可 ...

  8. Python之简单的用户名密码验证

    题目要求: 输入用户名密码 认证成功后显示欢迎信息 输错三次后锁定   #要求使用文件存储用户名和密码,每次从文件读入用户名和密码用来验证,如果输错三次密码该账户会被锁定,并讲锁定的用户名写入文件 # ...

  9. Ajax概述，封装以及联合模板引擎进行数据交互

    欢迎大家去博客冰山一树Sankey,浏览效果更好.直接右上角搜索该标题即可 博客园主页:博客园主页-冰山一树Sankey CSDN主页:CSDN主页-冰山一树Sankey 更多资料可参考Ajax 介绍 ...

  10. 关于http，测试面试官最爱问哪些？

    http和https的区别是什么? HTTP 是一种 超文本传输协议(Hypertext Transfer Protocol),而 HTTPS 的全称是 Hypertext Transfer Prot ...