单源最短路问题：OJ5——低德地图

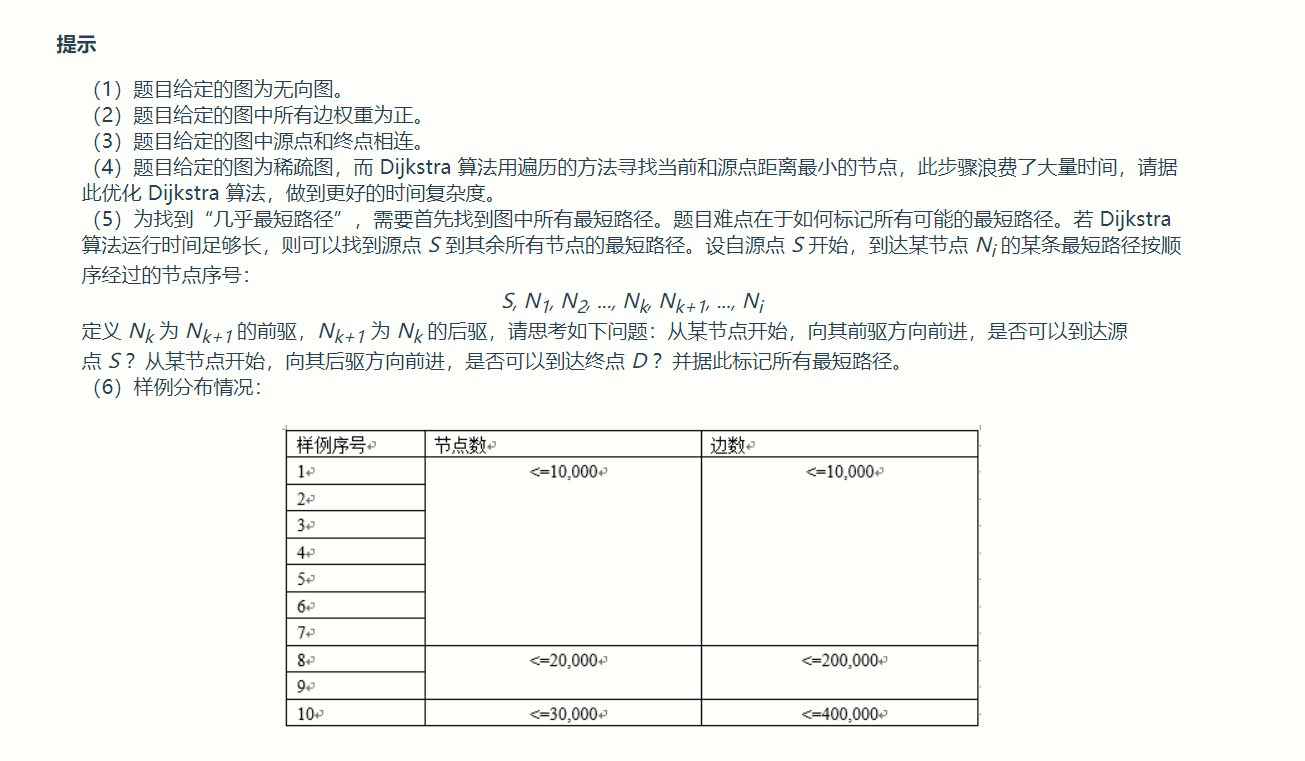
本题就是一道单源最短路问题。由于是稀疏图，我们采用Dijkstra算法。

Dijkstra算法原理

Dijkstra算法的步骤

我们把所有的节点分为两个集合：被选中的（visited==1） 和 未被选中的（visited==0），对于每个点，我们在操作中更新其到源点的距离。这个算法中用到贪心思想。
我们进行如下操作：
1.在所有未选中的节点中，找出目前距离源点距离最近的点，记为now，并将now移动到“被选中”集合（visited【now】=1）.
2.把所有和now相连的节点next的距离进行更新，取dis【now】+l和dis【next】的最小值，从而始终维护dis数组使得其中存储了目前选取点集合中的路径最小值。
3.从s开始循环上述步骤直至进行到d。
这样，我们就得到了最短路的长度dis【d】，同时可以记录最短路的路径：只需在上述2步骤中记录下next节点的最短路是从哪个节点找到了，再回溯回去即可。

Dijkstra贪心的证明

对于贪心算法，我们在使用的时候应该考虑其正确性。
首先，dijkstra算法只适用于正边权图，图中不能存在负值边（因为dijk算法只能对未被选中的点进行距离更新，而已经选中的点在存在负边的情况下可能存在更短路）
这里不给出详细的证明，证明参见：Dijkstra算法介绍+正确性证明+性能分析_月本_诚的博客-CSDN博客_dijkstra算法正确性证明我们只需要知道，对于一条最短路，它的从s1到s2的一部分就是s1到s2的最短路。这样，前面的算法就很好理解了。
可以采用归纳法证明，假设在Dijkstra算法中找到的最短路为V：v1v2.....vn，对于i<k原算法都正确，而在i=k时不正确。
这时我们考虑到我们在维护数组时保证了i=k继承了i=k-1的最短路，因此不可能存在前半部分是最短路，后面不是的情况。

Dijkstra的代码实现

这里直接给出本题的ac代码，再分别对不同的坑点进行解释。

#include<cstdio>
#include<cstdlib>
#include<vector>
#include<queue>
#include<utility>
using namespace std;
typedef pair<int,int> P;
struct node{vector<int> next;vector<int> length;}node[30005];
vector<int> path[30005][2];
vector<int> pre[30005][2];
int sum[2],n,m,s,d,pathsum=0;
void print(int i){
    printf("start\n");
    int li=path[1][i].size();for(int j=li-1;j>=0;j--)printf("%d\n",path[1][i][j]);
    printf("end\n");printf("%d\n",sum[i]);
}
void push(int now,int i,int ii){
    pathsum=i>pathsum?i:pathsum;
    path[i][ii].push_back(now);
    int ll=pre[now][ii].size();
    for(int j=0;j<ll;j++){
        int last=pre[now][ii][j];
        if(j)path[i+j][ii].push_back(now);
        push(last,i+j,ii);
    }
}
int dijk(int i){
    bool v[30005]={0};int dis[30005];priority_queue<P,vector<P>,greater<P>> calc;
    for(int i=0;i<=30000;i++){dis[i]=100000000;P x(100000000,i);calc.push(x);}
    int now;P x(0,s);calc.push(x);dis[s]=0;
    while(!v[d]){
        int min=100000000,minj=0;
        P x=calc.top();min=x.first;minj=x.second;calc.pop();
        while(v[minj]){P x=calc.top();min=x.first;minj=x.second;calc.pop();}
        now=minj;v[now]=1;if(min>=100000000)return 100000000;
        int l=node[now].next.size();
        for(int j=0;j<l;j++){
            int xx=node[now].next[j],ll=node[now].length[j];
            P x(dis[now]+ll,xx);calc.push(x);
            if(dis[now]+ll<dis[xx]){dis[xx]=dis[now]+ll;pre[xx][i].clear();pre[xx][i].push_back(now);}
            else if(dis[now]+ll==dis[xx])pre[xx][i].push_back(now);
        }
    }
    push(d,1,i);return dis[d];
}
int main(){
    scanf("%d%d",&n,&m);
    for(int i=1;i<=m;i++){
        int x,y,k;scanf("%d%d%d",&x,&y,&k);
        node[x].next.push_back(y);node[x].length.push_back(k);
        node[y].next.push_back(x);node[y].length.push_back(k);
    }
    scanf("%d%d",&s,&d);
    sum[1]=dijk(1);
    for(int q=1;q<=pathsum;q++){
        int l=path[q][1].size();
        for(int i=1;i<l;i++){
            int ss=path[q][1][i],dd=path[q][1][i-1];
            int ll=node[ss].next.size();int deltaj=0;
            for(int j=0;j<ll;j++){if(node[ss].next[j]==dd){deltaj=j;break;}}
            node[ss].length[deltaj]=100000000;
            int ll1=node[dd].next.size();int deltaj1=0;
            for(int j=0;j<ll;j++){if(node[dd].next[j]==ss){deltaj1=j;break;}}
            node[dd].length[deltaj1]=100000000;
        }
    }
    sum[0]=dijk(0);print(1);if(sum[0]<100000000&&sum[0]>sum[1])print(0);
}

首先这道题并不是要求我们找到最短路，而是要求找到所谓的“近似最短路”
它的要求是：不与任何一条最短路的任何一条边重合
因此我们的思路是：找到所有的最短路，并删除这些边。
下面我介绍一下我在做这道题的时候遇到的一些坑点：

如何找到所有的最短路？

我发现在我的dijk算法中，只能得到一条最短路，因为我起初用一个pre数组存储n个顶点在最短路中的上一个顶点，数组大小开了n，因此每个顶点只能存唯一一个pre点，也就不能得到所有的路。
后来，我在每个顶点处都开了一个vector，来记录所有可能的pre节点。

        int l=node[now].next.size();
        for(int j=0;j<l;j++){
            int xx=node[now].next[j],ll=node[now].length[j];
            P x(dis[now]+ll,xx);calc.push(x);
            if(dis[now]+ll<dis[xx]){dis[xx]=dis[now]+ll;pre[xx][i].clear();pre[xx][i].push_back(now);}
            else if(dis[now]+ll==dis[xx])pre[xx][i].push_back(now);
        }

然后我设计了一个递归函数来得到所有最短路中的边。但我并没有得到左右最短路，更像是得到了一棵由最短路组成的树，树根在终点d处。

void push(int now,int i,int ii){
    pathsum=i>pathsum?i:pathsum;
    path[i][ii].push_back(now);
    int ll=pre[now][ii].size();
    for(int j=0;j<ll;j++){
        int last=pre[now][ii][j];
        if(j)path[i+j][ii].push_back(now);
        push(last,i+j,ii);
    }
}

然后我再删掉这些边进行dijk寻路就可以了。

如何优化Dijkstra算法？

然而算法逻辑正确并不足够通过oj，目前的Dijkstra算法复杂度达到了惊人的O（n^2），tle也是必然的。
仔细思考之后，我想到每次寻找最近节点的步骤非常浪费时间：
原代码：

        int min=100000000,minj=0;
        for(int j=0;j<n;j++){if(min>dis[j]&&!v[j]){min=dis[j],minj=j;}}

而我们完全可以将当前的距离写进一个优先队列中，每次在这个最小堆中取最小值就可以了。至于更新的时候，如果有更小的值可以直接加入，无需删去原来的值，毕竟我们始终只会用到最小的值。
优化后代码如下：

P x=calc.top();min=x.first;minj=x.second;calc.pop();
while(v[minj]){P x=calc.top();min=x.first;minj=x.second;calc.pop();}

（其实是一个dowhile结构）
然后复杂度就降低到lgn了

彩蛋：附著名oier的ac代码如下

#include<bits/stdc++.h>
using namespace std;
#define N 33333
#define M 833333
#define ll long long
#define PI pair<ll,int>
#define pb push_back
#define mp make_pair
priority_queue<PI,vector<PI>,greater<PI>>q;
int fir[N],l[M],to[M],w[M],ec=1,ban[M],S,T;
void add(int a,int b,int v){l[++ec]=fir[a];fir[a]=ec;w[ec]=v;to[ec]=b;}
int n,m,pre[N],sta[N],tp; ll d[N],D[N];
int inSP[N];
void dijk(ll*d,int S,int T,int o){
    memset(d,0x3f,N<<3);
    q.push(mp(d[S]=0,S));
    while(q.size()){
        int x=q.top().second;
        ll D=q.top().first;
        q.pop();
        if(D^d[x])continue;
        for(int i=fir[x],y;i;i=l[i]){
            y=to[i];
            if(d[y]>D+w[i]&&!ban[i])
                q.push(mp(d[y]=D+w[i],y)),pre[y]=x;
        }
    }
    if(o&&d[T]<1e16){
        puts("start");
        int p=T;
        while(p^S) sta[++tp]=p=pre[p];
        while(tp) printf("%d\n",sta[tp--]);
        printf("%d\nend\n%lld\n",T,d[T]);
    }

}
int main(){
    cin>>n>>m;
    for(int i=0,a,b,W;i<m;++i)
        scanf("%d%d%d",&a,&b,&W),add(a,b,W),add(b,a,W);
    cin>>S>>T;
    dijk(d,S,T,2);
    dijk(D,T,S,0);
    for(int i=0;i<n;++i)
        inSP[i]=d[i]+D[i]==d[T];
    for(int i=2,x,y;i<=ec;++i){
        x=to[i^1];
        y=to[i];
        if(inSP[x]&&inSP[y]&&d[y]==d[x]+w[i])
            ban[i]=ban[i^1]=1;
    }
    dijk(d,S,T,1);
}