ACM - 最短路 - CodeForces 295B Greg and Graph

CodeForces 295B Greg and Graph

题解

$Floyd$ 算法是一种基于动态规划的算法，以此题为例介绍最短路算法中的 $Floyd$ 算法。

我们考虑给定一个图，要找出 $i$ 号点到 $j$ 号点的最短路径。则该最短路径只有两种可能：

$i$ 号点直接到达 $j$ 号点的路径中产生最短路径
$i$ 号点经过一些中间点到达 $j$ 号点的路径中产生最短路径

我们添加一个点 $k$，使得 $i$ 号点到 $j$ 号点再添加后产生的最短路径比添加前的最短路径更短，则称该操作为松弛。

下面我们以从一个示例开始介绍算法的步骤。

示例

给定一个赋权有向图，如下图：

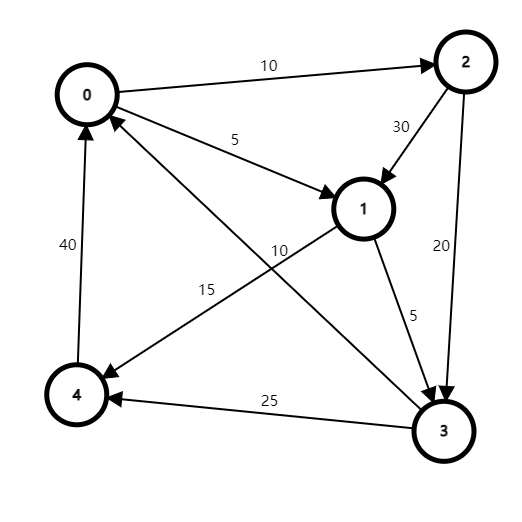
我们声明一个集合 $S$，并称该集合为中转集合。

我们声明一个 $dist$ 数组，其中 $dist[i][j]$ 表示从源点 $i$ 号点只经过中转集合中的点，到达目标点 $j$ 号点的最短路径。

每一轮更新都更新 $dist$，直到集合 $S$ 为图的顶点集 $V$。

初始化更新

$S$ 初始化为：

\[S = \{ \}
\]

$dist$ 数组根据我们的定义，此时 $dist[i][j]$ 表示不经过图中的任何顶点，直接从源点 $i$ 号点到达 $j$ 号点的最短距离，为了方便书写，我们此处采用图的邻接矩阵表示。

\[dist[i][j] = graph[i][j] \quad \forall i,j \in V
\]

故 $dist$ 被初始化为：

\[dist =
\begin{bmatrix}
0 & 5 & 10 & inf & inf \\
inf & 0 & inf & 5 & 15 \\
inf & 30 & 0 & 20 & inf \\
10 & inf & inf & 0 & 25 \\
40 & inf & inf & inf & 0
\end{bmatrix}
\]

第一轮更新

$S$ 更新为：

\[S = \{ 0 \}
\]

$dist$ 数组根据我们的定义，此时 $dist[i][j]$ 表示由图中 $0$ 号点中转，直接从源点 $i$ 号点到达 $j$ 号点的最短距离。该最短路径有两种可能：

最短路径经过 $0$ 号点；
最短路径不经过 $0$ 号点；

对于第 $1$ 种情况说明 $0$ 号点可以松弛之前的最短距离。这两种情况可以统一表示为下式：

\[\begin{align}
dist[i][j] = \min \left( dist[i][j],dist[i][0] + dist[0][j] \right) \quad \forall i,j \in V \tag{1}
\end{align}
\]

此处我们应该注意一下更新的顺序问题，上式表达的含义应该是指只由上一轮的 $dp[i][j]$、$dp[i][0]$ 和 $dp[0][j]$ 来更新出这一轮的 $dp[i][j]$。更准确地说应该可以扩展下数组 $dist$ 的维度。如下图所示：

其中 $k$ 表示这是第 $k$ 轮更新。按我们的意思，应该写成：

\[dist[i][j][1] = \min \left( dist[i][j][0],dist[i][0][0] + dist[0][j][0] \right) \quad \forall i,j \in V
\]

即只由第 $0$ 轮的 $dp[i][j]$、$dp[i][0]$ 和 $dp[0][j]$ 来更新出第 $1$ 轮的 $dp[i][j]$。那我们为什么可以写成式 $1$ 的样子？原因在于 $dp[i][0]$ 和 $dp[0][j]$ 在此轮更新循环中，始终都没有被更新。后面会更详细地说明这个问题。

故 $dist$ 被更新为：

\[dist =
\begin{bmatrix}
0 & 5 & 10 & inf & inf \\
inf & 0 & inf & 5 & 15 \\
inf & 30 & 0 & 20 & inf \\
10 & 15* & 20* & 0 & 25 \\
40 & 45* & 50* & inf & 0
\end{bmatrix}
\]

第二轮更新

$S$ 更新为：

\[S = \{ 0, 1 \}
\]

$dist$ 数组根据我们的定义，此时 $dist[i][j]$ 表示从源点 $i$ 号点出发，只经过中转集合 $S$ 中的点，到达 $j$ 号点的最短距离。该最短路径有两种可能：

最短路径经过 $1$ 号点；
最短路径不经过 $1$ 号点；

对于第 $1$ 种情况说明 $1$ 号点可以松弛之前的最短距离。这两种情况可以统一表示为下式：

\[dist[i][j] = \min \left( dist[i][j],dist[i][1] + dist[1][j] \right) \quad \forall i,j \in V
\]

我们接着就要问了，为什么经过 $1$ 号点的最短路径距离等于 $dist[i][1] + dist[1][j]$。在第一轮更新的时候容易想到，但这轮更新（第二轮更新）中，该问题需要仔细思考一下。

经过 $1$ 号点的路径这样表示：$i$(源点) $\to$ $1$ $\to$ $j$(目标点)。而经过 $1$ 号点的最短路径一定是由 $i$ 到 $1$ 的最短路径和 $1$ 到 $j$ 的最短路径构成（反证法即可得）。

我们应用这个性质，重新表述为：经过 $1$ 号点的从源点 $i$ 出发，由 $S - \{1\}$ 集合中转到达目标点 $j$ 的最短路径一定是由从源点 $i$ 出发，由 $S - \{1\}$ 集合中转到达目标点 $1$ 的最短路径和从源点 $1$ 出发，由 $S - \{1\}$ 集合中转到达目标点 $j$ 的最短路径构成（正确性显然，只是由原来的范围全路径集合缩小为$S - \{1\}$ 集合中转的那些路径构成的集合）。

而此轮更新仍然不会改变 $dist[i][1]$ 和 $dist[1][j]$ 的值，因此不用关心更新顺序的问题。

综上，上式完全正确。故 $dist$ 应该被更新为：

\[dist =
\begin{bmatrix}
0 & 5 & 10 & 10* & 20* \\
inf & 0 & inf & 5 & 15 \\
inf & 30 & 0 & 20 & 45* \\
10 & 15 & 20 & 0 & 25 \\
40 & 45 & 50 & 50* & 0
\end{bmatrix}
\]

第三轮更新

$S$ 更新为：

\[S = \{ 0, 1, 2\}
\]

状态转移方程为：

\[dist[i][j] = \min \left( dist[i][j],dist[i][2] + dist[2][j] \right)
\]

状态转移方程的正确性证明完全同上，而由归纳法容易知道对之后的更新该状态转移方程仍然正确。而该轮仍然不会改变 $dist[i][2]$ 和 $dist[2][j]$ 的值，因此不用关心更新顺序的问题。

故 $dist$ 应该被更新为：

\[dist =
\begin{bmatrix}
0 & 5 & 10 & 10 & 20 \\
inf & 0 & inf & 5 & 15 \\
inf & 30 & 0 & 20 & 45 \\
10 & 15 & 20 & 0 & 25 \\
40 & 45 & 50 & 50 & 0
\end{bmatrix}
\]

第四轮更新

$S$ 被更新为：

\[S = \{ 0, 1, 2, 3 \}
\]

$dist$ 被更新为：

\[dist =
\begin{bmatrix}
0 & 5 & 10 & 10 & 20 \\
15* & 0 & 25* & 5 & 15 \\
30* & 30 & 0 & 20 & 45 \\
10 & 15 & 20 & 0 & 25 \\
40 & 45 & 50 & 50 & 0
\end{bmatrix}
\]

第五轮更新

$S$ 被更新为：

\[S = \{ 0, 1, 2, 3, 4 \}
\]

$dist$ 被更新为：

\[dist =
\begin{bmatrix}
0 & 5 & 10 & 10 & 20 \\
15 & 0 & 25 & 5 & 15 \\
30 & 30 & 0 & 20 & 45 \\
10 & 15 & 20 & 0 & 25 \\
40 & 45 & 50 & 50 & 0
\end{bmatrix}
\]

此时 $S$ 集合等于图的顶点集 $V$。停止迭代。

最后得到的 $dist[i][j]$ 就表示源点 $i$ 到达目标点 $j$ 的最短路径距离。

程序设计

为了能清晰严谨的说明，我们可以将 $dist[i][j]$ 设成 $dist[i][j][k]$。每次循环用 $dist[i][j][k - 1]$ 来更新 $dist[x][y][k]$（即用上一层的 $dist$ 来更新这一层的 $dist$）。但实际上，我们发现可以通过减少一个维度来减小空间复杂度，虽然这时我们要注意更新顺序的问题，但可以进一步发现每次迭代 $dist[i][m]$ 和 $dist[m][j]$ 都没有发生被更新为新值，即对应的 $dist$ 的第 $m$ 行和第 $m$ 列都没有发生变化，这可以使得更新顺序可以任意。

如下图展示了在某一次迭代中更新 $dist[3][4]$ 的过程，对应的公式描述为：

\[dist[3][4] = \min (dist[3][4], dist[3][1] + dist[1][4])
\]

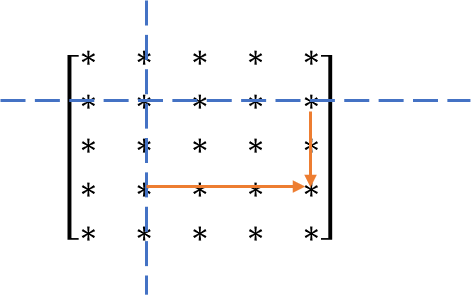
上图表示那次迭代过程中，第 $1$ 行和第 $1$ 列的值都没有被更新为新值，正是由此，明显可以看出 $dist[i][j]$ 的更新顺序确实可以任意。

程序的主要部分可以写出来：

// n : 表示图的顶点数

for (int k = 0; k < n; ++k) {

    for (int i = 0; i < n; ++i) {

        for (int j = 0; j < n; ++j) {

            dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j]);

        }

    }

}

最短路算法对比

算法	$Floyd$	$Dijkstra$	$Bellman$-$Ford$
空间复杂度	$O$$(V^2)$	$O$$(E)$	$O$$(E)$
时间复杂度	$O$$(V^3)$	看具体实现	$O$$(VE)$
负权边时是否可以处理	可以	不能	可以
判断是否存在负权回路	不能	不能	可以

其中 $V$ 表示图的顶点数，$E$ 表示图的边数。

运用 $Floyd$ 算法解决该题

题目大意：每次删去一个点，求当前删去该点之前，所有点对最短路径之和。

在每删除一个点前，题目明显要求求出的最短路径不是单源，而是多源的。具体地说，第一，针对所有当前存在的点对；第二，对每一对点对求最短路径。

每次删去一个点，直到把所有点都删尽。倒过来就相当于每次加入一个点，而恰好 $Floyd$ 算法的建立过程中 $dist$ 数组便记录了这些信息，所以逆序使用 $Floyd$ 算法即可。

程序：

#include<cstdio>

#include<cstring>

#include<algorithm>

#include<iostream>

#include<vector>

#include<queue>

using namespace std;

typedef pair<int, int> PII;

#define LL long long

int n, m;

int graph[505][505];  // 邻接矩阵存图

int del[505];         // 删除点的序号

LL sum[505];         // 删除点对前，点对的最短距离和

int dist[505][505];

int main()

{

    // 输入图的邻接矩阵

    cin >> n;

    for (int i = 1; i <= n; ++i) {

        for (int j = 1; j <= n; ++j) {

            cin >> m;

            graph[i][j] = m;

        }

    }

    // 输入图的顶点删除顺序

    for (int i = 1; i <= n; ++i) cin >> del[i];

    // 初始化 dist 数组

    memset(dist, 0x3f, sizeof(dist));

    for (int i = 1; i <= n; ++i) {

        for (int j = 1; j <= n; ++j) {

            dist[i][j] = graph[i][j];

        }

    }

    // 根据删除的点的序号，我们逆向添加点，运行Floyd算法

    int add[505];

    memset(add, 0, sizeof(add));

    for (int k = n; k >= 1; --k) {

        add[del[k]] = 1;

        for (int i = 1; i <= n; ++i) {

            for (int j = 1; j <= n; ++j) {

                dist[i][j] = min(dist[i][j], dist[i][del[k]] + dist[del[k]][j]);

            }

        }

        for (int i = 1; i <= n; ++i) {

            for (int j = 1; j <= n; ++j) {

                if (add[i] && add[j]) sum[k] += dist[i][j];

            }

        }

    }

    for (int k = 1; k <= n; ++k) printf("%I64d ", sum[k]);

    printf("\n");

    return 0;

}