Codeforces Round #786 (Div. 3) 补题记录

小结：

A,B,F 切，C 没写 1ll 对照样例才发现，E,G 对照样例过，D 对照样例+看了其他人代码（主要急于看后面的题，能调出来的但偷懒了。

---

CF1674A Number Transformation

考虑若 \(y\) 不能整除 \(x\) 则无解，否则一定存在一组解 \(a=1,b=y\div x\)。

#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(false)
#define TIE cin.tie(0),cout.tie(0);
#define int long long
using namespace std;
int T,n,a[200005],x,y ;
string s;
void solve(){
	cin>>x>>y;
	if(y%x){
		cout<<"0 0"<<endl;
		return ;
	}
	int tmp=y/x;
	cout<<1<<' '<<tmp<<endl;
}
signed main(){
	IOS;TIE;
	T=1;
	cin>>T;
	while(T--) solve();
	return 0;
}

---

CF1674B Dictionary

直接用 \(\text{map}\) 映射，用两个字符或字符串对应数字，注意两个字符相同的要跳过。

#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(false)
#define TIE cin.tie(0),cout.tie(0);
#define int long long
#define mk(x,y) make_pair(x,y)
using namespace std;
int T,n,a[200005],x,y,tot;
string s;
map<pair<char,char>,int> mp;
void solve(){
	cin>>s;
	cout<<mp[mk(s[0],s[1])]<<endl;
}
signed main(){
	IOS;TIE;
	T=1;
	for(char i='a';i<='z';i++){
		for(char j='a';j<='z';j++){
			if(i==j) continue;
			mp[mk(i,j)]=++tot;
		}
	}
	cin>>T;
	while(T--) solve();
	return 0;
}

---

CF1674C Infinite Replacement

分类讨论：

• 若替换串中有 a，且替换串长度 \(>1\)，则可以无限替换，输出 \(-1\)
• 若替换串中有 a，且替换串长度 \(=1\)，则只有一种情况，即原串
• 否则，考虑原串中每一位是否替换，可能情况有 \(2^{原串长度}\) 种情况

#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(false)
#define TIE cin.tie(0),cout.tie(0);
#define int long long
#define mk(x,y) make_pair(x,y)
using namespace std;
int T;
string s,t;
void solve(){
	cin>>s>>t;
	bool fl=0;
	for(int i=0;i<t.size();i++){
		if(t[i]=='a') fl=1;
	}
	if(fl&&t.size()>1){
		cout<<-1<<endl;
		return ;
	}
	if(fl){
		cout<<1<<endl;
		return ;
	}
	cout<<(1ll<<s.size())<<endl;
}
signed main(){
	IOS;TIE;
	cin>>T;
	while(T--) solve();
	return 0;
}

---

CF1674D A-B-C Sort

容易发现这样操作之后只可以改变相邻两个数的位置，若原长度为奇数则第一个数会多出来，否则看两两是否相等即可。

#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(false)
#define TIE cin.tie(0),cout.tie(0);
#define int long long
#define mk(x,y) make_pair(x,y)
using namespace std;
int T,n,a[200005],b[200005];
int l[1000005],r[1000005];
void solve(){
	cin>>n;
	for(int i=1;i<=n;i++) cin>>a[i],b[i]=a[i];
	sort(b+1,b+n+1);
	if(n%2){
		if(a[0]!=b[0]){
			cout<<"NO"<<endl;
			return ;
		}
	}
	for(int i=1+(n%2);i<=n;i+=2){
		if(!(a[i]==b[i]&&a[i+1]==b[i+1]||a[i]==b[i+1]&&a[i+1]==b[i])){
			cout<<"NO"<<endl;
			return ;
		}
	}
	cout<<"YES"<<endl;
}
signed main(){
	IOS;TIE;
	cin>>T;
	while(T--) solve();
	return 0;
}

---

CF1674E Breaking the Wall

分类讨论：

1. 取原串中最小的两个数 \(x,y\)（不一定相邻），使它们变零。分别一直 \(-2\)，代价为 \(⌈\frac{x}{2}⌉+⌈\frac{y}{2}⌉\)
2. 取原串中相邻两个数 \(a_i,a_{i+1}\)，使他们变零。设 \(x\) 为较大数，\(y\) 为较小数：
   1. 若 \(x>y\times2\)，则一直在 \(x\) 处 \(-2\)，代价为 \(y+⌈\frac{x-2\times y}{2}⌉\)
   2. 否则，看大小灵活 \(-2\)，代价为 \(⌈\frac{x+y}{3}⌉\)
3. 取原串中间隔一数的两个数 \(a_i,a_{i+2}\)，使他们变零。设 \(x\) 为较大数，\(y\) 为较小数。先一直使中间数 \(-2\) 直到 \(x,y\) 中任意一个变 \(0\)，随后剩下的一直 \(-2\)，代价为 \(y+⌈\frac{x-y}{2}⌉\)

去三种情况的最小答案即可。

#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(false)
#define TIE cin.tie(0),cout.tie(0);
#define int long long
#define mk(x,y) make_pair(x,y)
using namespace std;
int T,n,a[200005],ans=1e18,mn,semn;
void case0(){
	mn=semn=1e18;
	for(int i=1;i<=n;i++){
		if(a[i]<mn) semn=mn,mn=a[i];
		else if(a[i]<semn) semn=a[i];
	}
	ans=min(ans,(int)ceil(mn/2.0)+(int)ceil(semn/2.0));
}
void case1(){
	for(int i=1;i<n;i++){
		int x=a[i],y=a[i+1];
		if(x<y) swap(x,y);
		if(y*2<x) ans=min(ans,y+(int)ceil((x-y*2)/2.0));
		else ans=min(ans,(int)ceil((x+y)/3.0));
	}
}
void case2(){
	for(int i=1;i<n-1;i++){
		int x=a[i],y=a[i+2];
		ans=min(ans,min(x,y)+(int)ceil(abs(x-y)/2.0));
	}
}
void solve(){
	cin>>n;
	for(int i=1;i<=n;i++) cin>>a[i];
	case0();case1();case2();
	cout<<ans<<endl;
}
signed main(){
	IOS;TIE;
	T=1;
	while(T--) solve();
	return 0;
}

---

CF1674F Desktop Rearrangement

题意实为要求将所有 * 移动到这种状态：

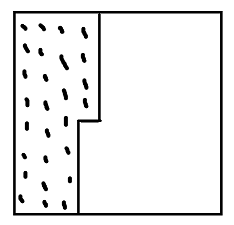
即优先填满靠左的列。

所以每次要做的就是统计出当前棋盘上有多少 *，这是左侧该有 * 的数量，然后算出该有 * 的位置有多少是空的，即为最小移动步数。

考虑对于每一列维护前缀和，每次更新一个点加一列，询问只要从左往右扫即可。

#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(false)
#define TIE cin.tie(0),cout.tie(0);
#define int long long
#define mk(x,y) make_pair(x,y)
using namespace std;
int T,n,m,x,y,q,s[1005][1005],sum;
bool a[1005][1005];
char c;
void solve(){
	cin>>n>>m>>q;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			cin>>c;
			if(c=='*') a[i][j]=1,sum++;
		}
	}
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++) s[i][j]=s[i-1][j]+a[i][j];
	}
	while(q--){
		cin>>x>>y;
		if(a[x][y]){
			sum--;
			for(int i=x;i<=n;i++) s[i][y]--;
		}
		else{
			sum++;
			for(int i=x;i<=n;i++) s[i][y]++;
		}
		a[x][y]^=1;
		int tmp=sum,ans=0;
		for(int j=1;j<=m;j++){
			if(tmp>n) tmp-=n,ans+=n-s[n][j];
			else{
				ans+=tmp-s[tmp][j];
				break;
			}
		}
		cout<<ans<<endl;
	}
}
signed main(){
	IOS;TIE;
	T=1;
	while(T--) solve();
	return 0;
}

---

CF1674G Remove Directed Edges

首先手玩样例，可以发现一个性质：删边之后若可以从 \(u\to v\)，则需满足 \(u\) 的出度 \(>1\)，\(v\) 的入度 \(>1\)。

同时，\(\text{DAG}\) 中要取一个点集，使可以从其中一点走向另一点，则此点集一定可以构成一条链。具体可以根据拓扑序来理解。

所以，就可以用拓扑排序求最长路的方法来做这道题。不同的是，有入度、出度 \(>1\) 的限制条件。具体处理方法是：记下每一个点的原始入度 \(In_i\) ，如果当前队首出度 \(<2\)，则按照常规拓扑排序的来搞，否则，若走向点的原始入度 \(>1\)，则可以更新那个点的答案。同时，减入度和入队还是和一般拓排序一样。

#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(false)
#define TIE cin.tie(0),cout.tie(0);
#define int long long
#define mk(x,y) make_pair(x,y)
using namespace std;
int T,n,m,in[200005],In[200005],out[200005],f[200005],u,v,ans;
bool vis[200005];
vector<int> a[200005];
queue<int> q;
void solve(){
	cin>>n>>m;
	for(int i=1;i<=m;i++){
		cin>>u>>v;
		a[u].push_back(v);
		in[v]++,In[v]++,out[u]++;
	}
	for(int i=1;i<=n;i++) if(!in[i]) vis[i]=1,q.push(i);
	for(int i=1;i<=n;i++) f[i]=1;
	while(q.size()){
		int k=q.front();q.pop();
		if(out[k]<2){
			for(int i=0;i<a[k].size();i++){
				int tmp=a[k][i];
				if(!--in[tmp]) q.push(tmp);
			}
			continue;
		}
		for(int i=0;i<a[k].size();i++){
			int tmp=a[k][i];
			if(In[tmp]>1) f[tmp]=max(f[tmp],f[k]+1);
			if(!--in[tmp]) q.push(tmp);
		}
	}
	for(int i=1;i<=n;i++) ans=max(ans,f[i]);
	cout<<ans<<endl;
}
signed main(){
	IOS;TIE;
	T=1;
	while(T--) solve();
	return 0;
}

---

\[\]

\[\Huge{G\ L\ \&\ H\ F\ !}
\]