NOIP2011普及组

T2  统计单词数

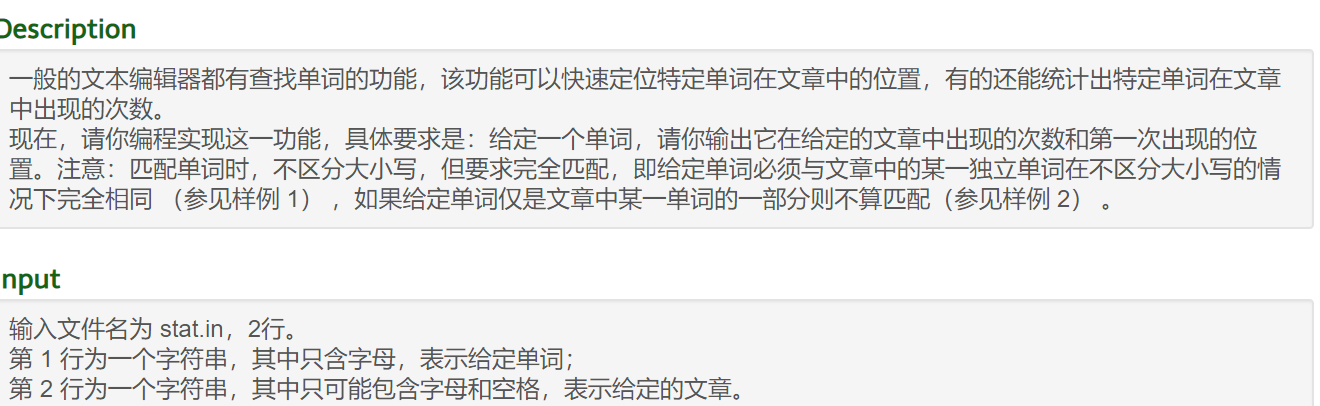
也是一道经典题

字符串匹配

#include<iostream>
#include<cstdio>
#include<map>
#include<vector>
#include<cstring>
using namespace std;
string a;
string jus;
int main(){
	getline(cin,a);
	getline(cin,jus);
	//含有空格的字符串输入
	int lenw=a.length();
	int lena=jus.length();
	for(int i=0;i<lenw;i++) {
		if(a[i]>='a'&&a[i]<='z') a[i]-=32;
	}
	for(int j=0;j<lena;j++) {
		if(jus[j]>='a'&&jus[j]<='z') jus[j]-=32;
		}
	int sum=0,pos=-1;
	for(int i=0;i<=lena-lenw;i++){ //注意上限
	int j;   //呜呜呜呜要自闭了这个要写在外面，因为j在后面判断
		for(j=0;j<lenw;++j){
			if(a[j]!=jus[i+j]) break;
			if(i>0&&jus[i-1]!=' ') break; //如果不是单词开头就结束
		}
			if(j==lenw&&(jus[i+j]==' '||i+j==lena)) {  //!!!!!
				sum++;
				if(sum==1) pos=i ;
			}
		}
	if(sum==0) cout<<"-1"<<endl;
	else cout<<sum<<" "<<pos<<endl;
	return 0;
}

　　

T3  瑞士轮

归并排序的思想，（没想到吧）这些事基础要掌握的东西啊！！！
每打完一轮后，都要通过归并排序的思想再次确定一个顺序表（2*N)的，然后在顺序表中确定这一次的输赢结果，分别放在win,lose里面，然后再放在顺序表中

#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<stack>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<set>
using namespace std;
const int maxn=200002;
const int INF=0x3fffffff;
//这道题用了归并排序的思想，排两个有序表，这两个有序表就是处理之后的输赢表
//处理好输赢表(根据能力）之后，需要再次排序（根据分数），也就是设置两个下标i，j，这样就是归并排序的思想，直接用sort的话会超时
struct node{
	int fen; //分数
	int rank;
	int power;  //能力
};
node win[maxn],lose[maxn],d[maxn];
int n,r,q;
bool cmp(node a,node b){
	if(a.fen!=b.fen) return a.fen>b.fen;
	else return a.rank<b.rank;
}

void guibing(){
	int i=0,j=0;
	int index=-1;
	//对有序的输赢表进行排序，用分数来排序
	while(1){
		if(i==n/2){
			//把lose剩下的全部放进去
			for(int k=j;k<i;k++){
				index++;
				d[index]=lose[k];
			}
			break;
		}
		else if(j==n/2){
		//把win剩下的全部放进去
			for(int k=i;k<j;k++){
				index++;
				d[index]=win[k];
			}
			break;
		}
		else{
			if(win[i].fen<lose[j].fen||(win[i].fen==lose[j].fen&&win[i].rank>lose[j].rank)){
				index++;
				d[index]=lose[j];
				j++;
			}
			else{
				index++;
				d[index]=win[i];
				i++;
			}
		}
	}
}

int main(){
	scanf("%d %d %d",&n,&r,&q);
	n*=2;
	for(int i=0;i<n;i++){
		scanf("%d",&d[i].fen);
		 d[i].rank=i;
	}
	for(int i=0;i<n;i++) scanf("%d",&d[i].power);
	sort(d,d+n,cmp);
	for(int j=0;j<r;j++){
		for(int i=0;i<n;i+=2){
			int t1=d[i].power,t2=d[i+1].power,t3=i/2;
			if(t1>t2){
				win[t3]=d[i];
				lose[t3]=d[i+1];
				win[t3].fen++;
			}
			else{
				win[t3]=d[i+1];
				lose[t3]=d[i];
				win[t3].fen++;
			}
		}
		guibing();

	//	cout<<endl;
	}
	printf("%d\n",d[q-1].rank+1);

return 0;
}

　　

T4  表达式的值

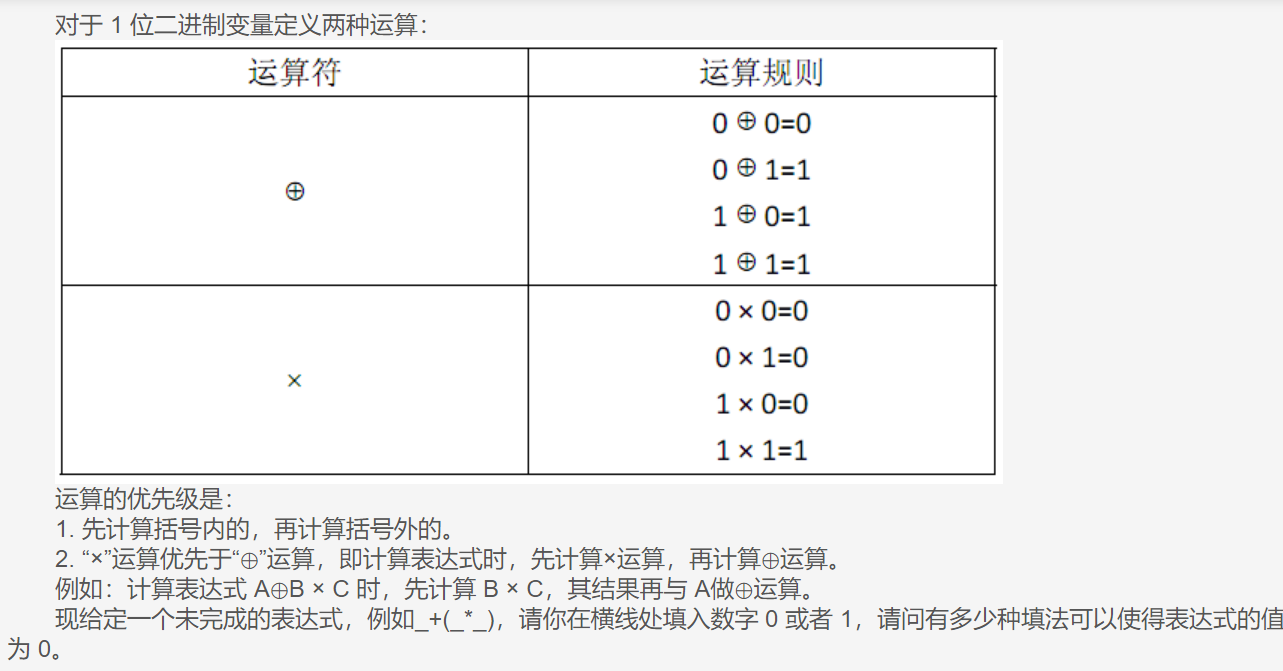
是一道没有头绪的题目

通过保存计算结果（上一步的）

首先这道题目，我们要先搞清楚我们如何从前往后退出答案。可以肯定的是，在出现某个特定符号的时候，我们要知道如何从已知答案中推出之后的答案。这其实就是一个用公式递推的过程。每一步计算下一步答案为0或1的方法数：设两个步骤的运算结果经过每个符号到一个结果时，第一个运算结果算出0的方案数为t1，1的方案数为t2。第二个算出0的方案数为t3，算出1的方案数为t4，则有： 当符号是“⊕”时，得到0的方案数为t1*t3，1的方案数：t1*t4+t2*t3+t2*t4 当符号是“×”时，得到0的方案数为t1*t3+t1*t4+t2*t3，1的方案数：t2*t4 用一个栈记录下来即可。

然后按以下方法计算：

1. 如果是左括号，就直接进栈；
2. 如果是右括号，就一直弹栈并加以计算，直到弹到左括号；
3. 如果是运算符，则弹栈，直到这个运算符的优先级大于符号栈栈顶的符号的优先级 或是左括号或栈空，然后将运算符进栈； 最后再将栈中残余的符号和结果一直弹到只剩一个结果，这个就是最后的结果。

#include <bits/stdc++.h>
const int M=10007,N=100005;
int n, u[N], v[N], top, k;
char c[N], S[N], ans[2*N];
int main()
{
    scanf("%d",&n);
    scanf("%s",c);
    ans[++k]='.';
    for(int i = 0; c[i]; i++)
    {
        if(c[i] == '(' || c[i] == '*')
            S[++top] = c[i];
        if(c[i] == '+')
        {
            while(S[top] == '*')
                ans[++k] = S[top--];
            S[++top] = c[i];
        }
        if(c[i] == ')')
        {
            while(S[top] != '(')
                ans[++k] = S[top--];
            top--;
        }
        if(c[i] != '(' && c[i] != ')')
            ans[++k]='.';
    }
    while(top > 0)
        ans[++k] = S[top--];
    for(int i = 1; i <= k; i++)
    {
        if(ans[i] == '.')
        {
            u[++top] = 1;
            v[top] = 1;
        }
        if(ans[i] == '*')
        {
            top--;
            u[top] = (u[top+1]*v[top]+u[top]*v[top+1]+u[top]*u[top+1])%M;
            v[top] = v[top]*v[top+1]%M;
        }
        if(ans[i] == '+')
        {
            top--;
            v[top] = (u[top+1]*v[top]+u[top]*v[top+1]+v[top]*v[top+1])%M;
            u[top] = u[top]*u[top+1]%M;
        }
    }
    printf("%d",u[1]);
    return 0;
}