用SQL实现统计报表中的"小计"与"合计"的方法详解

本篇文章是对使用SQL实现统计报表中的"小计"与"合计"的方法进行了详细的分析介绍，需要的朋友参考下

 

客户提出需求，针对某一列分组加上小计，合计汇总。网上找了一些有关SQL加合计的语句。都不是很理想。决定自己动手写。
思路有三个：
1.很多用GROUPPING和ROLLUP来实现。
  优点：实现代码简洁，要求对GROUPPING和ROLLUP很深的理解。
  缺点：低版本的Sql Server不支持。

2.游标实现。
  优点：思路逻辑简洁。
  缺点：复杂和低效。

3.利用临时表。
  优点：思路逻辑简洁，执行效率高。SQL实现简单。
  缺点：数据量大时耗用内存.

综合三种情况，决定“利用临时表”实现。
实现效果
原始表TB

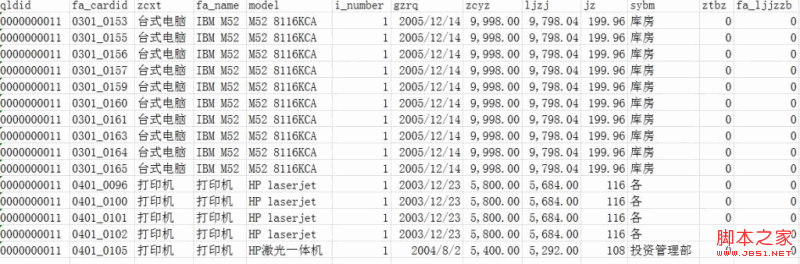
加上小计，合计后效果

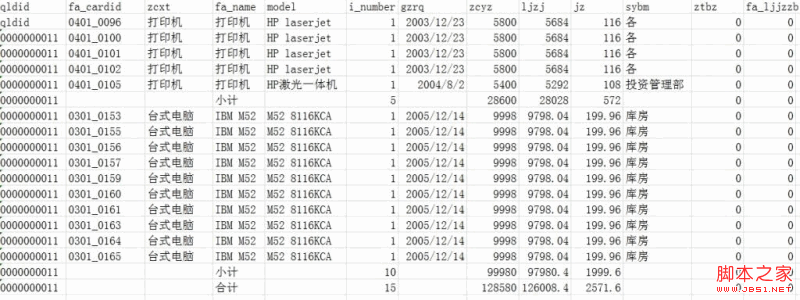
SQL语句

复制代码 代码如下:

select * into #TB from TB
select * into #TB1 from #TB where 1<>1
select distinct zcxt into #TBype from #TB order by zcxt
select identity(int,1,1)  fid,zcxt into #TBype1 from #TBype
DECLARE @i int
DECLARE @k int

select @i=COUNT(*) from #TBype
 set @k=0
  DECLARE @strfname varchar(50)
 WHILE @k < @i
  BEGIN
   Set @k =@k +1
   select @strfname=zcxt from #TBype1 where fid =@k
   set IDENTITY_INSERT #TB1 ON
      insert into #TB1(fid,qldid,fa_cardid,ztbz,fa_name,model,i_number,gzrq,zcyz,ljzj,jz,sybm,zcxt,fa_ljjzzb)
       select fid,qldid,fa_cardid,ztbz,fa_name,model,i_number,gzrq,zcyz,ljzj,jz,sybm,zcxt,fa_ljjzzb from
      (
   select * from #TB where zcxt=@strfname
   union all
        
select 0 fid,'' qldid,'' fa_cardid,'' ztbz,'小计' fa_name,''
model,sum(i_number) as i_number,'' gzrq,sum(CAST(zcyz as money)) as
zcyz,sum(CAST(ljzj as money)) as ljzj,sum(CAST(jz as money)) as jz,''
sybm,'' zcxt,Sum(fa_ljjzzb) as fa_ljjzzb
   from #TB where zcxt=@strfname
   group by ztbz
  ) as B
 set IDENTITY_INSERT #TB1 off
  END
select qldid,fa_cardid,zcxt,fa_name,model,i_number,gzrq,zcyz,ljzj,jz,sybm,ztbz,fa_ljjzzb from #TB1
union all
select
'' qldid,'' fa_cardid,'' ztbz,'合计' fa_name,'' model,sum(i_number) as
i_number,'' gzrq,sum(CAST(zcyz as money)) as zcyz,sum(CAST(ljzj as
money)) as ljzj,sum(CAST(jz as money)) as jz,'' sybm,''
zcxt,Sum(fa_ljjzzb) as fa_ljjzzb
from #TB
drop table #TB1
drop table #TBype1
drop table #TBype
drop table #TB

扩展改进
可以改写成一个通用的添加合计小计的存储过程