算法导论练习6.5-8 k路合并

题目：

请给出一个时间为O(nlgk)、用来将k个已排序链表合并为一个排序链表的算法。此处n为所有输入链表中元素的总数。（提示：用一个最小堆来做k路合并。

　看到题目第个想到的是归并排序过程中的归并操作子过程，从头开始两两比较，找出最小的，然后接着往后比较，常用的是2路归并。而题目给的是k个已排好序的链表(k>=2)。如果没有提示，我半天不知道如何去实现，幸好提示说用最小堆来做k路合并，于是我想到可以这样做：创建一个大小为k的数组，将k个链表中的第一个元素依次存放到数组中，然后将数组调整为最小堆，这样保证数组的第一个元素是最小的，假设为min，将min从最小堆取出并存放到最终结果的链表中，此时将min所在链表的下一个元素到插入的最小堆中，继续上面的操作，直到堆中没有元素为止。举个例子如下图所示（只给出不部分操作）：

最终结果如下图所示：

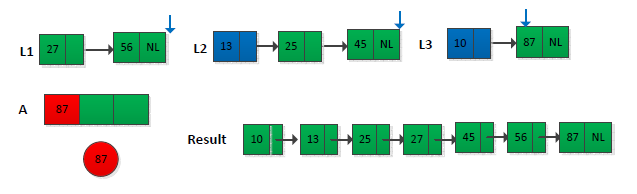
现在采用C++语言，借助STL实现此过程，链表采用list，最小堆中存放的是list的迭代器，表示list中元素的位置。完整程序如下：

#include <iostream>
#include <vector>
#include <list>
#include <iterator>
#include <cstdlib>
using namespace std;

template<class T> class MinHeap
{
public:
    MinHeap();
    MinHeap(const size_t size);
    ~MinHeap();
    T get_min() const;
    void delete_min();
    void insert_element(const T& e);
    void adjust_min_heap(const size_t i);
    size_t get_heap_size() const;
    int compare(const T& t1,const T& t2);
private:
    T *heap;
    size_t heap_size;
};

template<class T>
MinHeap<T>::MinHeap():heap(NULL),heap_size(){}

template<class T>
MinHeap<T>::MinHeap(const size_t size)
{
    if(!heap)
        delete [] heap;
    heap = new T[size+];
    heap_size = ;
}

template<class T>
MinHeap<T>::~MinHeap()
{
    if(!heap)
        delete [] heap;
    heap_size = ;
}

template<class T>
T MinHeap<T>::get_min() const
{
    if(heap_size > )
        return heap[];
    else
        return T();
}

template<class T>
void MinHeap<T>::delete_min()
{
    if(heap_size > )
    {
        heap[] = heap[heap_size];
        heap_size = heap_size - ;
        adjust_min_heap();
    }
    else
    {
        cout<<"Error: the min heap is empty"<<endl;
    }
}

template<class T>
void MinHeap<T>::insert_element(const T& e)
{
    size_t i,parent;
    T temp;
    heap_size = heap_size + ;
    heap[heap_size] = e;
    i = heap_size;
    parent = i/;
    while(i> && compare(heap[parent],heap[i]) > )
    {
        temp = heap[parent];
        heap[parent] = heap[i];
        heap[i] = temp;
        i = parent;
        parent = i/;
    }
}

template<class T>
void MinHeap<T>::adjust_min_heap(const size_t i)
{
    size_t left,right,least;
    T temp;
    left = i*;
    right = i*+;
    if(left <= heap_size && compare(heap[left],heap[i]) < )
        least = left;
    else
        least = i;
    if(right <= heap_size && compare(heap[right],heap[least]) < )
        least = right;
    if(least != i)
    {
        temp = heap[least];
        heap[least] = heap[i];
        heap[i] = temp;
        adjust_min_heap(least);
    }
}
template<class T>
size_t MinHeap<T>::get_heap_size() const
{
    return heap_size;
}

template<class T>
int MinHeap<T>::compare(const T& t1,const T& t2)
{
    return (*t1-*t2);
}

const static int k = ;

int main()
{

    list<int> lists[k];
    list<int>::iterator iters[k];
    list<int> retlist;
    list<int>::iterator retiter;
    list<int>::iterator iter;
    MinHeap<list<int>::iterator> minheap(k);

    //first list <12,24,52>
    lists[].push_back();
    lists[].push_back();
    lists[].push_back();
    cout<<"First list: ";
    for(iter=lists[].begin();iter != lists[].end();++iter)
          cout<<*iter<<"->";
    cout<<"NULL"<<endl;
    //second list <9,32>
    lists[].push_back();
    lists[].push_back();
    cout<<"Second list: ";
    for(iter=lists[].begin();iter != lists[].end();++iter)
          cout<<*iter<<"->";
    cout<<"NULL"<<endl;
    //third list <34,42,78>
    lists[].push_back();
    lists[].push_back();
    lists[].push_back();
    cout<<"Third list: ";
    for(iter=lists[].begin();iter != lists[].end();++iter)
          cout<<*iter<<"->";
    cout<<"NULL"<<endl;
    iters[] = lists[].begin();
    iters[] = lists[].begin();
    iters[] = lists[].begin();

    minheap.insert_element(iters[]);
    minheap.insert_element(iters[]);
    minheap.insert_element(iters[]);

    while(minheap.get_heap_size())
    {
        iter = minheap.get_min() ;
        retlist.push_back(*iter);
        minheap.delete_min();
        ++iter;
        if(iter != lists[].end() && iter != lists[].end()
           &&iter != lists[].end())
            minheap.insert_element(iter);
    }
    cout<<"Merge the there list is: "<<endl;
    for(retiter = retlist.begin();retiter!= retlist.end();retiter++)
        cout<<*retiter<<"->";
    cout<<"NULL"<<endl;
    exit();
}

测试结果：

转自：http://www.cnblogs.com/Anker/archive/2013/01/24/2874569.html

我按照上面的写了代码，总是遇到错误说：在画红线的地方

if(it!=lists[0].end() && it!=lists[1].end() && it!=lists[2].end())：

总是报错:list iterator incompatible:

#include<iostream>
#include<string>
#include<list>
#include<algorithm>
using namespace std;

int left(int i) { return *i;}
int right(int i){ return *i+;}
int parent(int i) { return i/;}

template<class T>
class MinHeap
{
private:
    T *heap;
    int heapSize;
public:

    MinHeap(const int size);
    ~MinHeap();

    void adjustMinHeap(int i);

    void insert(const T& e);
    T extractMin();
    T getMin();
    void deleteMin();

    void print();
    int getHeapSize(){ return heapSize;}
    int comp(const T& a,const T& b) { return (*a)-(*b);}
};

template<class T>
MinHeap<T>::MinHeap(const int size)
{
    heap=new T[size+];
    heapSize=;
}
template<class T>
MinHeap<T>::~MinHeap()
{
    delete[] heap;
    heapSize=;
}

template<class T>
void MinHeap<T>::insert(const T& e)
{
    heapSize++;
    heap[heapSize]=e;//从这可以看出第0个不存
    int i=heapSize;
    int parentNode=parent(i);
    while(i> && comp(heap[parentNode],heap[i])>) //注意，T里面的类型为Iter迭代器类型，不能是这么来比较heap[parentNode]>heap[i].
    {
        swap(heap[parentNode],heap[i]);
        i=parentNode;
        parentNode=parent(i);
    }
}

template<class T>
void MinHeap<T>::adjustMinHeap(int i)
{
    int l=left(i);
    int r=right(i);
    int smallest;
    if(l<=heapSize && comp(heap[l],heap[i])< )//l<=heapSize必须在前面，为什么，因为如果在后面,heap[l]将访问冲突
        smallest=l;
    else
        smallest=i;
    if(r<=heapSize && comp(heap[r],heap[smallest])<)
        smallest=r;

    if(smallest!=i)
    {
        swap(heap[i],heap[smallest]);
        adjustMinHeap(smallest);
    }
}
template<class T>
T MinHeap<T>::extractMin()
{
    T min=heap[];
    heap[]=heap[heapSize];
    heapSize--;
    adjustMinHeap();
    return min;
}

template<class T>
T MinHeap<T>::getMin()
{
    if(heapSize>)
        return heap[];
    else
        return T();
}

template<class T>
void MinHeap<T>::deleteMin()
{
    heap[]=heap[heapSize];
    heapSize--;
    adjustMinHeap();
}

template<class T>
void MinHeap<T>::print()
{
    for(int i=;i<=heapSize;i++)
        cout<<*heap[i]<<ends;
    cout<<endl;
}

//#define k 3
const  int k=;
int main()
{
    //验证MinHeap正确性
    /*
    MinHeap<int> heap(4);
    heap.insert(4);
    heap.insert(3);
    heap.insert(1);
    heap.insert(2);
    heap.print(); //1 2 3  4
    cout<<"min:"<<heap.extractMin()<<endl; //1
    heap.print(); //2 4 3
    */

    list<int> lists[k];
    typedef list<int>::iterator Iter;
    Iter iters[k];

    MinHeap<Iter> minHeap(k);

    //first list<12,24,52>
    lists[].push_back();
    lists[].push_back();
    lists[].push_back();
    cout<<"First list: ";
    Iter it;
    for(it=lists[].begin();it!=lists[].end();it++)
        cout<<*it<<"->";
    cout<<"NULL"<<endl;

     //second list <9,32>
    lists[].push_back();
    lists[].push_back();
    cout<<"Second list: ";
    for(it=lists[].begin();it != lists[].end();++it)
          cout<<*it<<"->";
    cout<<"NULL"<<endl;

     //third list <34,42,78>
    lists[].push_back();
    lists[].push_back();
    lists[].push_back();
    cout<<"Third list: ";
    for(it=lists[].begin();it != lists[].end();++it)
          cout<<*it<<"->";
    cout<<"NULL"<<endl;

    iters[]=lists[].begin();
    iters[]=lists[].begin();
    iters[]=lists[].begin();

    minHeap.insert(iters[]);
    minHeap.insert(iters[]);
    minHeap.insert(iters[]);
    minHeap.print();
    list<int> retlist;
    while(minHeap.getHeapSize()!=)//这个条件最开始没想到
    {
        it=minHeap.getMin();
        retlist.push_back(*it);
        minHeap.deleteMin();
        ++it;

        if(it!=lists[0].end() && it!=lists[1].end() && it!=lists[2].end())
        {
            minHeap.insert(it);
        }
    }
    cout<<"Merge list:"<<endl;
    for(it=retlist.begin();it!=retlist.end();it++)
        cout<<*it<<"->";
    cout<<"NULL"<<endl;

}

搞了2-3个小时没有找到原因，暂时放一放。