LR、Poly2、FM、FFM

1. LR

LR的linear Margin：

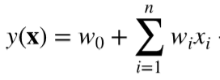
假设特征之间是相互独立的，忽略了feature pair等高阶信息；在LR中，特征组合等高阶信息是通过特征工程在特征侧引入的，那么有哪些模型不需要通过特征工程自动学习高阶信息呢？

2. Degree-2 Polynomial Margin (Poly2)

在LR基础上，加入任意两个特征之间的关系：

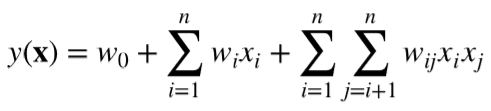
其中，w_ij是feature pair （i,j）的权重，只有xi和xj都非零时，组合特征xixj才有意义。

组合特征的参数一共有n(n-1)/2个，任意两个参数都是独立的。然而，在数据稀疏性普遍存在的实际应用场景中，二次项参数的训练是很困难的。其原因是，每个参数wij的训练需要大量xi和xj都非零的样本；由于样本数据本来就比较稀疏，满足“xi和xj都非零”的样本将会非常少。训练样本的不足，很容易导致参数wij不准确，最终将严重影响模型的性能。

相对于Linear Margin，Poly2存在如下两个问题：

（1）参数空间大幅增加，由线性增加至平方级；

（2）但样本仍然非常稀疏。

假设直接使用Poly2穷举feature pair进行训练，则会存在如下两个致命问题：

（1）参数过多导致训练算法效率极低，甚至内存溢出；

（2）由于特征大量增加但不增加样本，极容易造成过拟合。

因此，我们需要一种在模型侧计算高阶信息的低复杂度方法，也就是下面要介绍的FM。

3. FM（Factorization Machine）

　　 FM将wij分解为两个向量的内积：

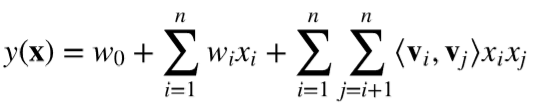
　　其中，vi是一个k维向量。直观上看，FM的复杂度为O(kn²)，但是通过下式，FM的二次项可以化简，其复杂度可以优化到O(kn)。由此可见，FM可以在线性时间对新样本做出预测。

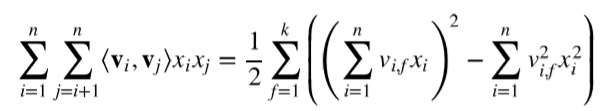
　　直观来看，FM认为当一个特征  需要与其它特征  考虑组合特性的时候，只需要一组k维向量  即可代表  ，而不需针对所特征分别计算出不同的组合参数  。这相当于将特征映射到一个k维空间，用向量关系表示特征关系：某种程度上来说，映射到k维空间上，相似的向量会有相似的性质。

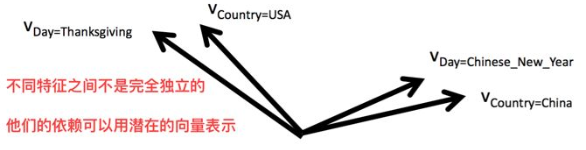
　　FM使用SGD训练模型，模型各个参数的梯度如下：

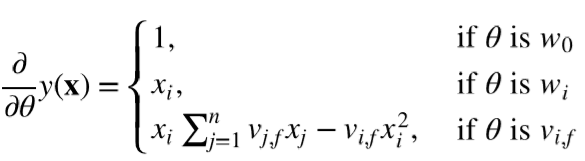
FM的优势：

• 应对稀疏数据--用vector乘积表示权重使得没有观察到的数据也可以被表示；
• 训练参数是线性的；
• 预测时间是线性的.

4. FFM（Field-aware Factorization Machine）

　　假设样本的n个特征属于f个field，那么FFM的二次项有nf个隐向量。而在FM模型中，每一维特征的隐向量只有一个。FM可以看做是FFM的特例，是把所有特征都归属到一个field时的FFM模型。根据FFM的field敏感特性，可以导出其模型方程。

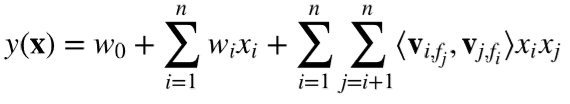
其中，f_j是第j个特征所属的field。如果隐向量的长度为k，那么FFM的二次参数有nfk个，远多于FM模型的nk个。此外，由于，隐向量与field相关，FFM二次项并不能化简，其预测复杂度是O(kn²)

举例：

这条记录可以编码成5个特征，其中“Genre=Comedy”和“Genre=Drama”属于同一个field，“Price”是数值型，不用one-hot编码转换。

那么，FFM的组合特征有10项，如下图所示：

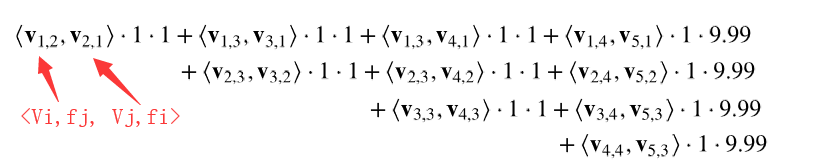
其中，二次项共有n(n-1)/2=5*4/2=10个

5. 总结

• Poly2：提供n个参数  ，n为特征数量；
• FM：提供1个k维参数  ，与对方特征的k维参数  作内积当做权重；
• FFM：提供m个k维参数  ，m为field的数量。也就是说，  会视和它组合的特征  属于哪个field来决定它使用哪一个k维向量参与内积计算。

参考文献：

【1】CTR预估[六]: Algorithm-Factorization Machine

【2】从FM推演各深度学习CTR预估模型（附代码）

【3】基于深度学习的CTR预估模型集合

【4】CTR预估[六]: Algorithm-Factorization Machine