1.打开Eclipse,依次点击“File” 、“New” 、“Other” ，选择生成动态Web项目。

2.输入项目名字，点击Finish

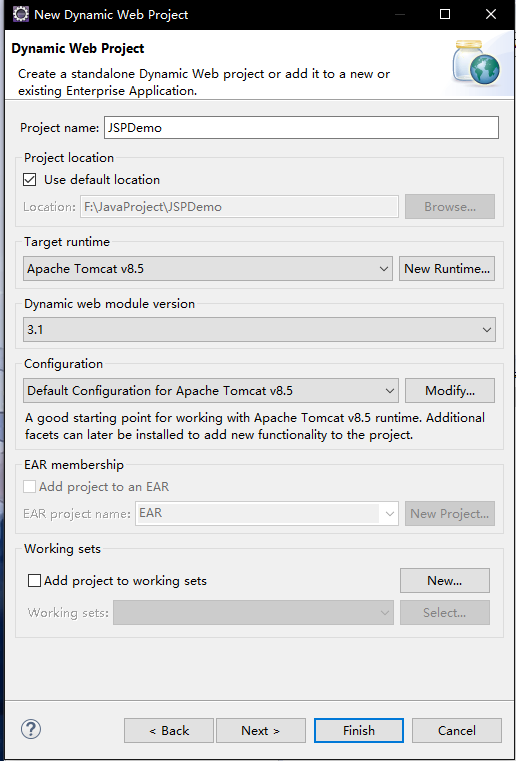
生成项目结构如下：

3.在WebContent目录上，单击右键，依次点击“”new“、 ”JSP File"

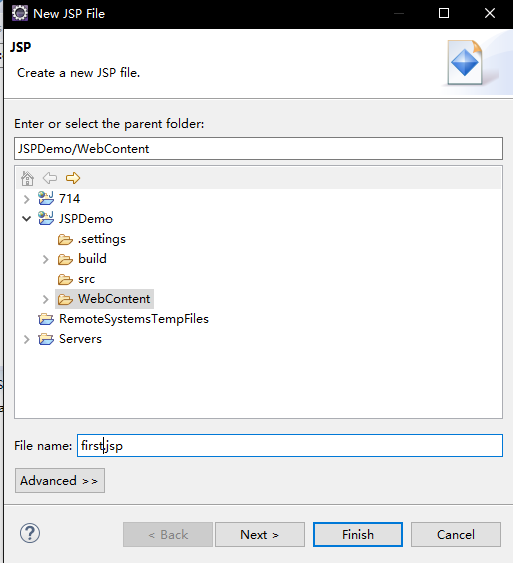
4.在新生成的jsp文件中添加如下第10-12行代码：

5.在生成的jsp文件上，单击右键，依次点击“Run as”、 “Run on server”，选择指定的服务器运行。

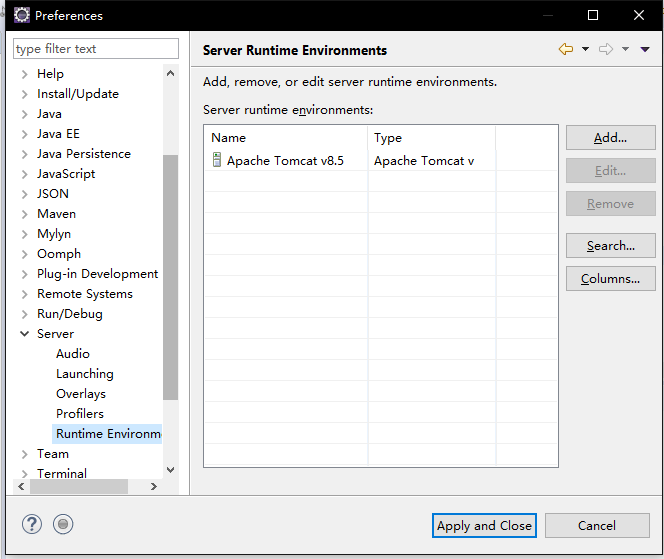
ps：服务器的配置可以在windows中的“Perferences“ ”Server" "Runtime Environments"进行配置

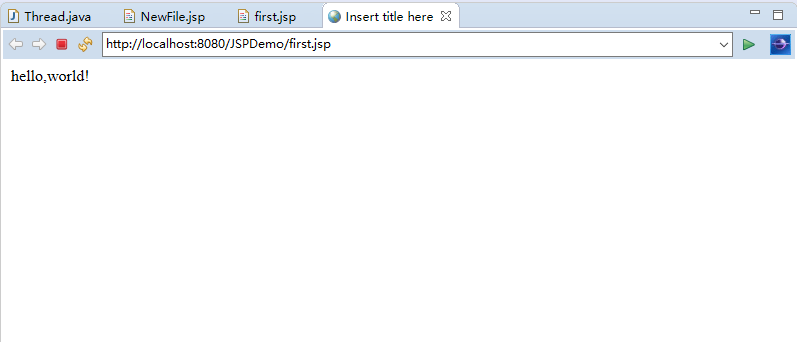
6.运行效果如下

第一节 简单的jsp实例的更多相关文章

  1. Chapter03 第一节 简单变量

    3.1 简单变量 定义一个变量后,系统根据变量类型的不同在内存的不同区域分配一个空间,将值复制到内存中,然后用户通过变量名访问这个空间. 3.1.1 变量名 变量名的命名规则: 只能使用字母.数字.下 ...

  2. 第一个简单的Echarts实例

    该示例使用 vue-cli 脚手架搭建 安装echarts依赖 npm install echarts -S 或者使用国内的淘宝镜像: 安装 npm install -g cnpm --registr ...

  3. 程序演示：C语言第一个简单实例

    在信息化.智能化的世界里,可能很早很早 我们就听过许多IT类的名词,C语言也在其中,我们侃侃而谈,到底C程序是什么样子?让我们先看简单的一个例子: 1 2 3 4 5 6 7 8 9 #include ...

  4. Qt5.9一个简单的多线程实例（类QThread）（第一种方法）

    Qt开启多线程,主要用到类QThread.有两种方法,第一种用一个类继承QThread,然后重新改写虚函数run().当要开启新线程时,只需要实例该类,然后调用函数start(),就可以开启一条多线程 ...

  5. 第一节：.Net版基于WebSocket的聊天室样例

    一. 说在前面的话 该篇文章为实时通讯系列的第一节,基于WebSocket编写了一个简易版聊天样例,主要作用是为引出后面SignalR系列的用法及其强大方便之处,通过这个样例与后续的SignalR对比 ...

  6. 第一节，TensorFlow基本用法

    一 TensorFlow安装 TensorFlow是谷歌基于DistBelief进行研发的第二代人工智能学习系统,其命名来源于本身的运行原理.Tsnsor(张量)意味着N维数组,Flow(流)意味着基 ...

  7. Ext JS学习第十六天 事件机制event（一） DotNet进阶系列(持续更新) 第一节：.Net版基于WebSocket的聊天室样例 第十五节：深入理解async和await的作用及各种适用场景和用法 第十五节：深入理解async和await的作用及各种适用场景和用法 前端自动化准备和详细配置(NVM、NPM/CNPM、NodeJs、NRM、WebPack、Gulp/Grunt、G

    code&monkey   Ext JS学习第十六天 事件机制event(一) 此文用来记录学习笔记: 休息了好几天,从今天开始继续保持更新,鞭策自己学习 今天我们来说一说什么是事件,对于事件 ...

  8. 第一节 课程简介与HTML5概述

    第一节 课程简介与HTML5概述 *********************************************************** 1.1课程简介 教学目的: 从基础入手到能够运 ...

  9. 第一节：《线程安全和锁Synchronized概念》

    第一节:线程安全和锁Synchronized概念 一.进程与线程的概念 (1)在传统的操作系统中,程序并不能独立运行,作为资源分配和独立运行的基本单位都是进程. 在未配置 OS 的系统中,程序的执行方 ...

随机推荐

  1. K3CLOUD替代方案

    路径 [生产制造]->[工程数据]->[替代方案]->[替代方案] 应用场景 实际业务处理中,由于订单取消.工程变更.客户需求变化.预测或计划不准确等原因造成原材料库存积压.呆滞,使 ...

  2. python模块_pcharm导入包的问题

    1.添加pip包 2.导入项目需要由内置包(library root)

  3. sql优化问题笔记（mysql）

    相信大家平时面试都会遇到这个问题:平时你都是怎么对sql进行调优的? 此篇文章相当于一个随便笔记,根据朋友们的聊天记录整理而成,如有不对,请指正! 注意:这篇是以mysql整理的 查看sql计划分析 ...

  4. Chrome disable cache & clear memory cache

    Chrome disable cache & clear memory cache disable cache

  5. 华为5G在印度被禁

    前段时间,澳大利亚政府以“担心外国渗透”为由,决定禁止华为为建设新的5G网络提供设备.这让大家不禁猜测,难道华为的5G真的被国外市场禁入了? 对此,华为表达出了极大的失落感,并在一份声明中称,“政府告 ...

  6. POJ1860（Currency Exchange）

    题意: 给出一张各种货币交换的网络,问在网络中交换原有的货币,问货币能否增值? 解析: 判断是否存在正环即可  用spfa  负环和正环的判定方法一样  如果一个点的进队次数超过n次 则存在环 代码如 ...

  7. Mysql读写分离php脚本

    <?php/*php如何连接mysql*/ /*$link = mysql_connect(‘localhost‘, ‘root‘, ‘‘);if (!$link) {die(‘Could no ...

  8. 自学工业控制网络之路1.6-典型的现场总线介绍Interbus

    返回 自学工业控制网络之路 自学工业控制网络之路1.6-典型的现场总线介绍Interbus 1987年正式公布,其主要技术开发者为德国的PhoenixContact公司.1996年,INTERBUS成 ...

  9. intent 几种用法

    Intent 应该算是Android中特有的东西.你可以在Intent中指定程序 要执行的动作(比如:view,edit,dial),以及程序执行到该动作时所需要的资料.都指定好后,只要调用start ...

  10. JAVA类中获取项目路径

    在java web项目中获取项目的src/main/resource下的文件路径 当前类名.class.getClassLoader().getResource("/").getP ...