斐波那契数列的生成 %1e8 后的结果

方法一  用数组开，一般开到1e7，1e8 左右的数组就是极限了   对时间也是挑战

#include<bits/stdc++.h>
using namespace std;
const int maxn=1e8+;
int a[maxn];
int32_t main()
{
    a[]=;
    a[]=;
    for(int i=;i<maxn;i++)
    a[i]=a[i-]%+a[i-]%;
    cout<<a[maxn-]<<endl;
}

方法二  求第多少个斐波那契数      时间还是个问题

#include<bits/stdc++.h>
using namespace std;
const int maxn=1e8+;

int32_t main()
{
    int x; x=;
    if(x==) cout<<<<endl;
    if(x==) cout<<<<endl;
    if(x>)
    {
        int a=;
        int b=;
        int c=;
        for(int i=;i<=x;i++)
        {
            c=(a+b)%;
            a=b%;
            b=c;
        }
        cout<<c<<endl;
    }
}

方法三

通项公式 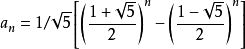            a[n]=1/sqrt(5)  (  ((1+sqrt(5))/2 )^n-((1-sqrt(5))/2)^n  )；

这不是重点   重要的是 矩阵 求斐波那契数列

不是很会矩阵    推荐这个博客 https://blog.csdn.net/flyfish1986/article/details/48014523

也可以看我的代码（看了过程再来看比较好）

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int k=1e8;
int fj(int n)
{
    if(n==) return ;
    int m=n-;
    int a11=,a12=,a21=,a22=;
    int t1=,t2=;
    int b11=,b12=,b21=,b22=;//  kau su mi de
    while(m)
    {
        if(m%==)
        {
            int c11=a11*b11+a12*b21;
            int c12=a11*b12+a12*b22;
            int c21=a21*b11+a22*b21;
            int c22=a21*b12+a22*b22;
            a11=c11%k;
            a12=c12%k;
            a21=c21%k;
            a22=c22%k;
            m--;
        }
        else if(m%==)
        {
            int c11=b11*b11+b12*b21;
            int c12=b11*b12+b12*b22;
            int c21=b21*b11+b22*b21;
            int c22=b21*b12+b22*b22;
            b11=c11%k;
            b12=c12%k;
            b21=c21%k;
            b22=c22%k;
            m=m/;
        }
    }
    return a11;
}

int32_t main()
{
    int n;
    cin>>n;
    int c=fj(n);
    cout<<c<<endl;
}

{  f[n+1]  f[n] }  ={ 1 1}  ^n

{  f[n]  f[n-1}     = {1 0}

#include<iostream>
#include<cstdio>
using namespace std;
const int maxn=1e5+;
const int mod=;
int MOD=mod;
struct Matrix {
    int a[][];
    void init() {
        for (int i = ; i < ; i++) {
            for (int j = ; j < ; j++)
                a[i][j] = ;
        }
    }
    void _init() {
        init();
        for (int i = ; i < ; i++) a[i][i] = ;
    }
}A, B;

Matrix mul(Matrix a, Matrix b) {
    Matrix ans;
    ans.init();
    for (int i = ; i <; i++) {
        for (int j = ; j < ; j++) {
            if(a.a[i][j]) {
                for (int k = ; k <; k++) ans.a[i][k] = (ans.a[i][k] + 1LL * a.a[i][j] * b.a[j][k]) % MOD;
            }
        }
    }
    return ans;
}
Matrix q_pow(Matrix a, int k) {
    Matrix ans;
    ans._init();
    if(k <= ) return ans;
    while(k) {
        if(k&) ans = mul(ans, a);
        a = mul(a, a);
        k >>= ;
    }
    return ans;
}
int main(){
    int n,m;
    while(){
        scanf("%d",&n); if(n==-) break;
        Matrix a; a.init();
        a.a[][]=; a.a[][]=;
        a.a[][]=;
        a=q_pow(a,n);
        printf("%d\n",a.a[][]);
    }
}