NDArray自动求导

NDArray可以很方便的求解导数，比如下面的例子：（代码主要参考自https://zh.gluon.ai/chapter_crashcourse/autograd.html）

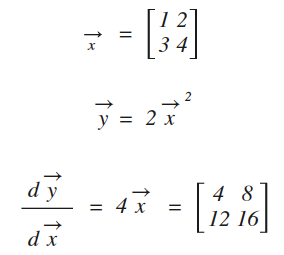
用代码实现如下：

 import mxnet.ndarray as nd
 import mxnet.autograd as ag
 x = nd.array([[1,2],[3,4]])
 print(x)
 x.attach_grad() #附加导数存放的空间
 with ag.record():
     y = 2*x**2
 y.backward() #求导
 z = x.grad #将导数结果(也是一个矩阵)赋值给z
 print(z) #打印结果

[[ 1.  2.]
 [ 3.  4.]]
<NDArray 2x2 @cpu(0)>

[[  4.   8.]
 [ 12.  16.]]
<NDArray 2x2 @cpu(0)>

对控制流求导

NDArray还能对诸如if的控制分支进行求导，比如下面这段代码：

 def f(a):
     if nd.sum(a).asscalar()<15: #如果矩阵a的元数和<15
         b = a*2 #则所有元素*2
     else:
         b = a
     return b

数学公式等价于：

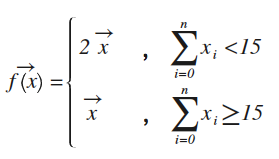
这样就转换成本文最开头示例一样，变成单一函数求导，显然导数值就是x前的常数项，验证一下：

import mxnet.ndarray as nd
import mxnet.autograd as ag

def f(a):
    if nd.sum(a).asscalar()<15: #如果矩阵a的元数和<15
        b = a*2 #则所有元素平方
    else:
        b = a
    return b

#注:1+2+3+4<15，所以进入b=a*2的分支
x = nd.array([[1,2],[3,4]])
print("x1=")
print(x)
x.attach_grad()
with ag.record():
    y = f(x)
print("y1=")
print(y)
y.backward() #dy/dx = y/x 即:2
print("x1.grad=")
print(x.grad)

x = x*2
print("x2=")
print(x)
x.attach_grad()
with ag.record():
    y = f(x)
print("y2=")
print(y)
y.backward()
print("x2.grad=")
print(x.grad)

x1=
[[ 1.  2.]
 [ 3.  4.]]
<NDArray 2x2 @cpu(0)>

y1=
[[ 2.  4.]
 [ 6.  8.]]
<NDArray 2x2 @cpu(0)>

x1.grad=
[[ 2.  2.]
 [ 2.  2.]]
<NDArray 2x2 @cpu(0)>

x2=
[[ 2.  4.]
 [ 6.  8.]]
<NDArray 2x2 @cpu(0)>

y2=
[[ 2.  4.]
 [ 6.  8.]]
<NDArray 2x2 @cpu(0)>

x2.grad=
[[ 1.  1.]
 [ 1.  1.]]
<NDArray 2x2 @cpu(0)>

头梯度

原文上讲得很含糊，其实所谓头梯度，就是一个求导结果前的乘法系数，见下面代码：

 import mxnet.ndarray as nd
 import mxnet.autograd as ag

 x = nd.array([[1,2],[3,4]])
 print("x=")
 print(x)

 x.attach_grad()
 with ag.record():
     y = 2*x*x

 head = nd.array([[10, 1.], [.1, .01]]) #所谓的"头梯度"
 print("head=")
 print(head)
 y.backward(head_gradient) #用头梯度求导

 print("x.grad=")
 print(x.grad) #打印结果

x=
[[ 1.  2.]
 [ 3.  4.]]
<NDArray 2x2 @cpu(0)>

head=
[[ 10.     1.  ]
 [  0.1    0.01]]
<NDArray 2x2 @cpu(0)>

x.grad=
[[ 40.           8.        ]
 [  1.20000005   0.16      ]]
<NDArray 2x2 @cpu(0)>

对比本文最开头的求导结果，上面的代码仅仅多了一个head矩阵，最终的结果，其实就是在常规求导结果的基础上，再乘上head矩阵（指：数乘而非叉乘)

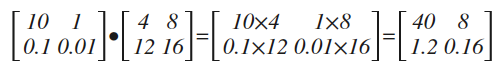
链式法则

先复习下数学

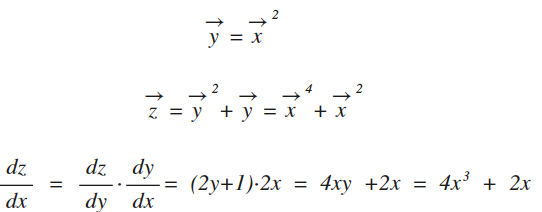
注：最后一行中所有变量x,y,z都是向量（即：矩形），为了不让公式看上去很凌乱，就统一省掉了变量上的箭头。NDArray对复合函数求导时，已经自动应用了链式法则，见下面的示例代码：

 import mxnet.ndarray as nd
 import mxnet.autograd as ag

 x = nd.array([[1,2],[3,4]])
 print("x=")
 print(x)

 x.attach_grad()
 with ag.record():
     y = x**2
     z = y**2 + y

 z.backward()

 print("x.grad=")
 print(x.grad) #打印结果

 print("w=")
 w = 4*x**3 + 2*x
 print(w) # 验证结果

x=
[[ 1.  2.]
 [ 3.  4.]]
<NDArray 2x2 @cpu(0)>

x.grad=
[[   6.   36.]
 [ 114.  264.]]
<NDArray 2x2 @cpu(0)>

w=
[[   6.   36.]
 [ 114.  264.]]
<NDArray 2x2 @cpu(0)>