图->存储结构->数组表示法(邻接矩阵)
文字描述
用两个数组分别存储顶点信息和边/弧信息。
示意图



算法分析
构造一个采用邻接矩阵作存储结构、具有n个顶点和e条边的无向网(图)G的时间复杂度是(n*n + e*n), 其中对邻接矩阵G.arcs的初始化耗费了n*n的时间。
借助于邻接矩阵容易判定两个顶点之间是否有边/弧相连,并容易求得各个顶点的度。对于无向图,顶点vi的度是邻接矩阵地i行(或第i列)的元素之和;对于有向图,第i行的元素之和为顶点vi的出度;第j列的元素之和为顶点vj的入度;
代码实现
/*
以数组表示法(邻接矩阵)作为图的存储结构创建图。
*/
#include <stdio.h>
#include <stdlib.h>
#include <string.h> #define INFINITY 100000 //最大值
#define MAX_VERTEX_NUM 20 //最大顶点数
typedef enum {DG, DN, UDG, UDN} GraphKind; //{有向图,有向网,无向图,无向网}
typedef int VRType;
typedef char VertexType;
typedef struct{
char note[];
}InfoType;
typedef struct ArcCell{
VRType adj; //顶点关系类型:1)对无权图,用1或0表示相邻否;2)对带权图,则为权值类型
InfoType *info; //该弧相关信息的指针
}ArcCell, AdjMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM];
typedef struct{
VertexType vexs[MAX_VERTEX_NUM]; //顶点向量
AdjMatrix arcs; //邻接矩阵
int vexnum, arcnum; //图的当前顶点数和弧数
GraphKind kind; //图的种类标志
}MGraph; /*
若G中存在顶点u,则返回该顶点在图中位置;否则返回-1。
*/
int LocateVex(MGraph G, VertexType v){
int i = ;
for(i=; i<G.vexnum; i++){
if(G.vexs[i] == v){
return i;
}
}
return -;
} /*
采用数组表示法(邻接矩阵),构造无向网
*/
int CreateUDN(MGraph *G){
int i = , j = , k = , IncInfo = ;
int v1 = , v2 = , w = ;
char tmp[] = {}; printf("输入顶点数,弧数,其他信息标志位: ");
scanf("%d,%d,%d", &G->vexnum, &G->arcnum, &IncInfo); for(i=; i<G->vexnum; i++){
printf("input vexs %d: ", i+);
memset(tmp, , sizeof(tmp));
scanf("%s", tmp);
G->vexs[i] = tmp[];
}
for(i=; i<G->vexnum; i++){
for(j=; j<G->vexnum; j++){
G->arcs[i][j].adj = INFINITY;
G->arcs[i][j].info = NULL;
}
}
for(k=; k<G->arcnum; k++){
printf("输入第%d条弧: 顶点1, 顶点2,权值", k+);
memset(tmp, , sizeof(tmp));
scanf("%s", tmp);
sscanf(tmp, "%c,%c,%d", &v1, &v2, &w);
i = LocateVex(*G, v1);
j = LocateVex(*G, v2);
G->arcs[i][j].adj = w;
if(IncInfo){
//
}
G->arcs[j][i] = G->arcs[i][j];
}
return ;
} /*
采用数组表示法(邻接矩阵),构造无向图
*/
int CreateUDG(MGraph *G)
{
int i = , j = , k = , IncInfo = ;
int v1 = , v2 = , w = ;
char tmp[] = {}; printf("输入顶点数,弧数,其他信息标志位: ");
scanf("%d,%d,%d", &G->vexnum, &G->arcnum, &IncInfo); for(i=; i<G->vexnum; i++){
printf("输入第%d个顶点: ", i+);
memset(tmp, , sizeof(tmp));
scanf("%s", tmp);
G->vexs[i] = tmp[];
}
for(i=; i<G->vexnum; i++){
for(j=; j<G->vexnum; j++){
G->arcs[i][j].adj = ;
G->arcs[i][j].info = NULL;
}
}
for(k=; k<G->arcnum; k++){
printf("输入第%d条弧(顶点1, 顶点2): ", k+);
memset(tmp, , sizeof(tmp));
scanf("%s", tmp);
sscanf(tmp, "%c,%c", &v1, &v2, &w);
i = LocateVex(*G, v1);
j = LocateVex(*G, v2);
G->arcs[i][j].adj = ;
if(IncInfo){
//
}
G->arcs[j][i] = G->arcs[i][j];
}
return ;
} /*
采用数组表示法(邻接矩阵),构造图
*/
int CreateGraph(MGraph *G)
{
printf("输入图类型: -有向图(0), -有向网(1), +无向图(2), +无向网(3): ");
scanf("%d", &G->kind);
switch(G->kind){
case DG://构造有向图
case DN://构造有向网
printf("还不支持!\n");
return -;
case UDG://构造无向图
return CreateUDG(G);
case UDN://构造无向网
return CreateUDN(G);
default:
return -;
}
} /*
输出图的信息
*/
void printG(MGraph G)
{
if(G.kind == DG){
printf("类型:有向图;顶点数 %d, 弧数 %d\n", G.vexnum, G.arcnum);
}else if(G.kind == DN){
printf("类型:有向网;顶点数 %d, 弧数 %d\n", G.vexnum, G.arcnum);
}else if(G.kind == UDG){
printf("类型:无向图;顶点数 %d, 弧数 %d\n", G.vexnum, G.arcnum);
}else if(G.kind == UDN){
printf("类型:无向网;顶点数 %d, 弧数 %d\n", G.vexnum, G.arcnum);
}
int i = , j = ;
printf("\t");
for(i=; i<G.vexnum; i++){
printf("%c\t", G.vexs[i]);
}
printf("\n");
for(i=; i<G.vexnum; i++){
printf("%c\t", G.vexs[i]);
for(j=; j<G.vexnum; j++){
if(G.arcs[i][j].adj == INFINITY){
printf("INF\t");
}else{
printf("%d\t", G.arcs[i][j].adj);
}
}
printf("\n");
}
} int main(int argc, char *argv[])
{
MGraph G;
if(CreateGraph(&G) > -)
printG(G);
return ;
}
邻接矩阵存储结构(图)
代码运行
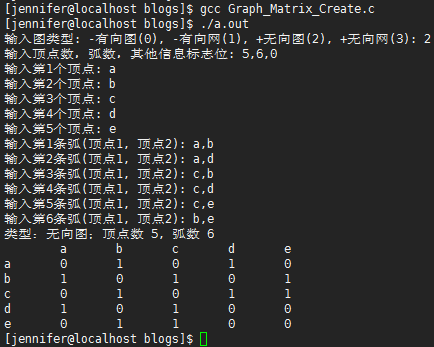
图->存储结构->数组表示法(邻接矩阵)的更多相关文章
- 图->存储结构->邻接表
文字描述 邻接表是图的一种链式存储结构.在邻接表中,对图中每个顶点建立一个单链表,第i个单链表的结点表示依附顶点vi的边(对有向图是指以顶点vi为尾的弧).单链表中的每个结点由3个域组成,其中邻接点域 ...
- 图->存储结构->邻接多重表
文字描述 邻接多重表是无向图的另一种链式存储结构. 虽然邻接表是无向图的一种很有效的存储结构,在邻接表中容易求得顶点和边的各种信息. 但是,在邻接表中每一条边(vi,vj)有两个结点,分别在第i个和第 ...
- 图->存储结构->十字链表
文字描述 十字链表是有向图的另一种链式存储结构. 在十字链表中,对应于有向图中每一条弧有一个结点,对应于每个顶点也有一个结点.这些结点的结构如下所示: 在弧结点中有5个域: 尾域tailvex和头域h ...
- 线性表(存储结构数组)--Java 实现
/*线性表的数组实现 *特点:插入删除慢需要平均移动一半的数据,查找较快 *注意:有重复和无重复的数据对应的操作会有些不同 *注意数组一旦创建其大小就固定了 *Java集合长度可变是由于创建新的数组将 ...
- 优先队列(存储结构数组)--Java实现
/*优先队列--是对队列的一种改进 *要存储的数据存在优先级--数值小的优先级高--在队头 *优先队列的实现 *1.数组:适合数据量小的情况(没有用rear+front实现) *优先队列头在items ...
- 队列(存储结构数组)--Java实现
/*队列:其实也是一种操作受限的线性表 *特点:先进先出 *队尾指针:负责元素的进队 *队头指针:负责元素的出队 *注意:普通队--容易浪费空间,一般队列使用最多的就是循环队列--指针环绕 *队列的实 ...
- 有序线性表(存储结构数组)--Java实现
/*有序数组:主要是为了提高查找的效率 *查找:无序数组--顺序查找,有序数组--折半查找 *其中插入比无序数组慢 * */ public class MyOrderedArray { private ...
- 【PHP数据结构】图的存储结构
图的概念介绍得差不多了,大家可以消化消化再继续学习后面的内容.如果没有什么问题的话,我们就继续学习接下来的内容.当然,这还不是最麻烦的地方,因为今天我们只是介绍图的存储结构而已. 图的顺序存储结构:邻 ...
- 存储结构与邻接矩阵,深度优先和广度优先遍历及Java实现
如果看完本篇博客任有不明白的地方,可以去看一下<大话数据结构>的7.4以及7.5,讲得比较易懂,不过是用C实现 下面内容来自segmentfault 存储结构 要存储一个图,我们知道图既有 ...
随机推荐
- mercurial的几个易用性小技巧
其实这两年,能够采用mercurial的项目我都尽量用,甚至有些上游是git的,或者需要托管到公司内gitlab上与别人协作的,我都装上hg-git.无它,只是因为mercurial易用性比git好得 ...
- 【九天教您南方cass 9.1】 13 等高线法计算土方量
同学们大家好,欢迎收看由老王测量上班记出品的cass9.1视频课程 我是本节课主讲老师九天. 我们讲课的教程附件也是共享的,请注意索取 在测量空间中. [点击索取cass教程]5元立得 (给客服说暗号 ...
- 小技巧 - CSS中:hover调试
在调试CSS的时候,我一般使用Chrome的F12开发者工具,或者FireFox的FireBug直接在元素上面修改好Style后,再写入到CSS中.前几天遇到一个问题就是a:hover,鼠标一移开效果 ...
- Android wpa_supplicant 四次握手 流程分析
记录wpa_supplicant四次握手的过程. 相关log:https://www.cnblogs.com/helloworldtoyou/p/9633603.html 接收到第一次握手,会设置一个 ...
- Mysql系列八:Mycat和Sharding-jdbc的区别、Mycat分片join、Mycat分页中的坑、Mycat注解、Catlet使用
一.Mycat和Sharding-jdbc的区别 1)mycat是一个中间件的第三方应用,sharding-jdbc是一个jar包 2)使用mycat时不需要改代码,而使用sharding-jdbc时 ...
- python风格的抽象工厂模式
抽象工厂模式: 提供一个接口,用户创建多个相关或依赖对象,而不需要指定具体类. 原则: 依赖抽象,不依赖具体类. 实例: 用不同原材料制作不同口味的披萨,创建不同原材料的工厂,不同实体店做出口味不同的 ...
- SharePreferences
SharePreferences是一种轻量级的数据存储方式,它是以key-value的形式保存在 data/data/<packagename>/shared_prefs 下的xml文件中 ...
- css预处理和bootstrap
css预处理框架的比较 http://www.oschina.net/question/12_44255?sort=default&p=4 bootstrap中文网 http://v3.boo ...
- [IR] Arithmetic Coding
Statistical methods的除了huffman外的另一种常见压缩方式. Huffman coding的非连续数值特性成为了无法达到香农极限的先天无法弥补的缺陷,但Arithmetic co ...
- J - 哈密顿绕行世界问题
一个规则的实心十二面体,它的 20个顶点标出世界著名的20个城市,你从一个城市出发经过每个城市刚好一次后回到出发的城市. Input 前20行的第i行有3个数,表示与第i个城市相邻的3个城市.第20行 ...
